Contoh Soal PAT Semester 2 Matematika IPA Kelas 11 dan Pembahasan

Buat menghadapi akhir semester genap, elo perlu mempelajari contoh soal PAT semester 2 Matematika IPA kelas 11 dan pembahasannya. Yuk, pelajari selengkapnya!

Halo, kakak kelas sekaligus adik kelas! Ciye, sebentar lagi jadi anak tertua di sekolahan nih….

Dulu, waktu gue masih sekolah, detik-detik kenaikan kelas 11 SMA bikin gue deg-degan. Soalnya, gue bakal jadi yang tertua di sekolah (tapi nggak literally yang paling tua juga, sih). Selain itu, tingkat kesulitan mata pelajaran juga bakal naik level.

Karena gue dulu juga merupakan anak penjurusan IPA, mata pelajaran yang bikin gue deg-degan waktu Penilaian Akhir Tahun (PAT) semester 2 adalah matematika. Hubungan gue sama Matematika ibarat asam manis gitu, deh. Kadang sayang, kadang ‘gemes’ kalau nggak nemu-nemu jawabannya.

So, buat elo yang mengambil penjurusan IPA, gue akan ngajak elo membedah contoh soal PAT semester 2 Matematika IPA kelas 11. Elo perlu pemanasan dengan mempelajari soal PAT semester 2 Matematika IPA kelas 11 dari materi semester genap.

Masih ingat nggak, apa aja materi semester 2 Matematika IPA kelas 11 dan gimana contoh soalnya? Yuk, langsung aja cekidot.…

Sekilas tentang Soal PAT Semester 2 Matematika IPA Kelas 11

Pada contoh soal PAT semester 2 Matematika IPA kelas 11 ini, gue akan membahas dari materi Matematika Peminatan kelas 11, yaitu bab persamaan lingkaran dan suku banyak.

Masing-masing bab punya tiga contoh soal yang akan dibahas. So, elo akan belajar enam contoh soal PAT semester 2 Matematika IPA kelas 11, beserta pembahasannya.

Langsung aja kita bahas masing-masing contoh soal PAT semester 2 Matematika IPA kelas 11, ya….

Topik Soal 1: Lingkaran

Lingkaran merupakan kumpulan dari titik-titik yang berbentuk lingkaran pada bidang datang. Kumpulan titik-titik ini punya jarak sama terhadap titik tengah yang disebut sebagai titik pusat.

Pada bab lingkaran, elo belajar tentang jarak dua titik, menghitung titik pusat dan jari-jari lingkaran, menentukan persamaan lingkaran, sampai persamaan garis singgung lingkaran.

Di bawah ini, ada tiga contoh soal PAT semester 2 Matematika IPA kelas 11 yang membahas tentang lingkaran. Yuk, coba kerjakan dan simak pembahasannya!

1. Suatu lingkaran berpusat di O(0,0). Jika lingkaran tersebut melalui titik (4,2), maka persamaan lingkaran tersebut adalah….

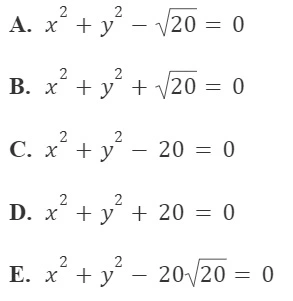
Jawaban: C

Pembahasan

Diketahui:

Pusat lingkaran = O(0,0). Anggap aja (0,0) adalah (a,b).

Lingkaran melalui titik (x,y), yaitu (4,2)

Persamaan lingkaran yang pusatnya (0,0) adalah

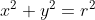
Karena belum jari-jarinya (R), kita cari dulu.

Rumus jari-jari lingkaran dengan pusat (0,0) dan melalui titik (4,2) adalah:

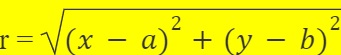
Kita masukin angka-angkanya ke dalam rumus.

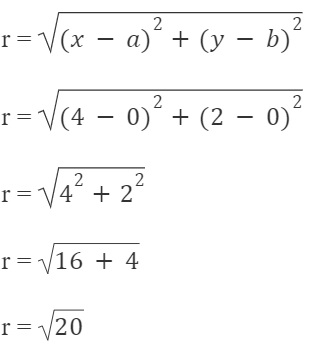
Tinggal kita masukin ke rumus persamaan lingkaran dengan pusat (0,0).

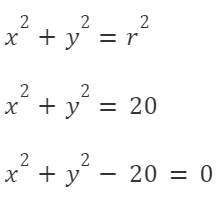
Jadi, jawabannya adalah C.

Kalau masih bingung, elo bisa baca materi Rumus Persamaan Lingkaran dan Contoh Soal – Materi Matematika Kelas 11.

2. Garis x + y = 3 menyinggung lingkaran L : x2+y2+2x-2y+k=0 untuk nilai k = ….

A. 2

B. 3

C. 5

D. – 5/2

E. – 5/3

Jawaban: D

Pembahasan

Diketahui, garis x + y = 3 menyinggung lingkaran L : x2+y2+2x-2y+k=0

Hubungan antara garis yang menyinggung lingkaran, kalau digambar jadi begini.

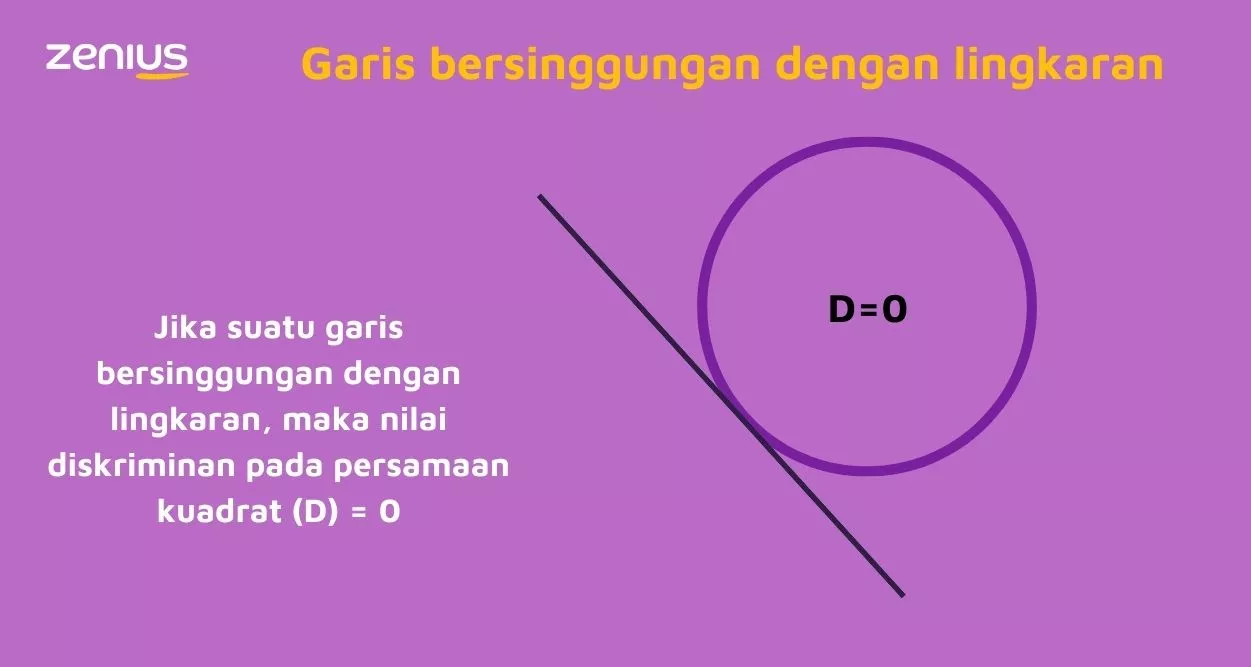
Yang ditanyakan adalah nilai k.

Buat mencari nilai k, elo bisa substitusikan garis ke persamaan lingkaran di atas.

Kita bikin y = 3 – x

Kalau disubstitusikan ke dalam persamaan lingkaran, maka

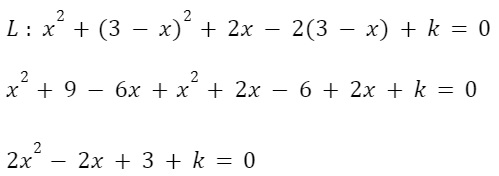
Dari persamaan kuadrat di atas, kita tentukan konstantanya.

a = 2

b = -2

c = 3+k

Kita balik ke gambar ilustrasi garis yang menyinggung lingkaran tadi. Kalau suatu garis menyinggung lingkaran yang punya persamaan kuadrat, maka D = 0. Kalau elo mau memahami lebih dalam lagi tentang diskriminan, elo bisa baca di sini.

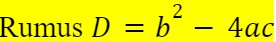
Kita masukin ke persamaannya.

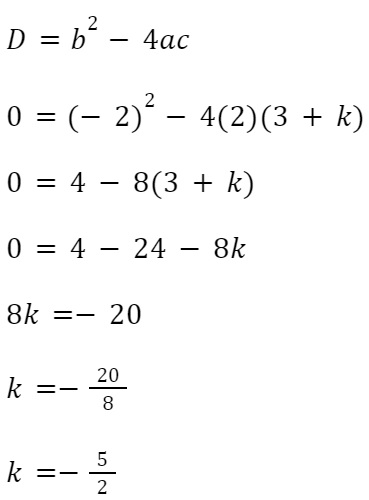
Jadi, jawabannya adalah D.

Baca Juga: Rumus Persamaan Garis Singgung Lingkaran dan Contoh Soal – Materi Matematika Kelas 11

3. Diberikan dua lingkaran dengan persamaan berikut,

L1 : x2+y2-10x+4y-20=0

L2 : x2+y2+14x-6y+22=0

Kedudukan kedua lingkaran tersebut adalah ….

A. saling lepas

B. bersinggungan di dalam

C. bersinggungan di luar

D. saling berpotongan

E. lingkaran yang sama

Jawaban: C

Pembahasan

Ada beberapa macam kedudukan lingkaran terhadap lingkaran lain. Elo bisa lihat gambarnya di bawah ini.

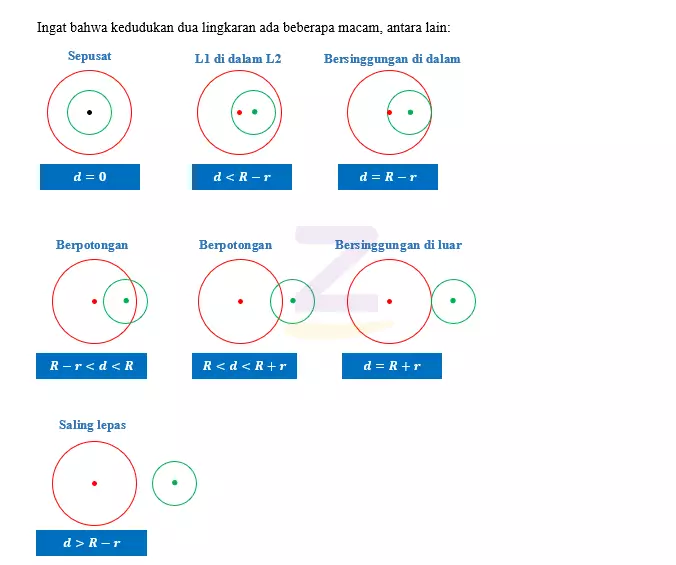
Terus, gimana caranya mengetahui kedudukan dua lingkaran?

Kalau pada soal belum ada titik pusat dan jari-jari kedua lingkaran, kita cari dulu keduanya.

Kita nyari titik pusat dan jari-jari lingkaran L1dulu.

L1 : x2+y2-10x+4y-20=0

Lingkaran ini merupakan bentuk umum persamaan kuadrat, yaitu darix2+y2+Ax+By+C=0

Di mana A = – 10, B = 4, C = – 20So, rumus mencari pusat lingkaran dari bentuk umum adalah:

Sekarang, kita cari titik pusat dan jari-jari L2.

L2 : x2+y2+14x-6y+22=0

L2 juga punya bentuk umum persamaan kuadrat. Dengan:

A = 14

B = -6

C = 22

Pusat lingkaran pada L2 adalah:

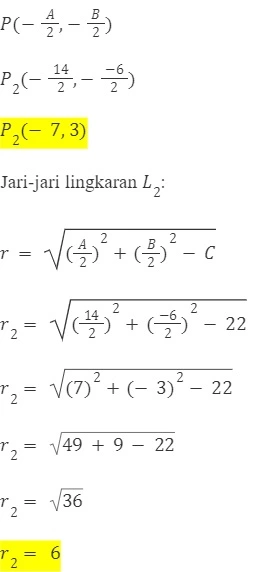
Sekarang, kita cari jarak antara dua pusat lingkaran.

Kita balik lagi ke beberapa macam kedudukan lingkaran tadi.

Manakah yang sesuai?

Coba jumlahkan antara r1 dan r2 dari hasil yang udah kita hitung tadi.

r1+r2=7+6

r1+r2=13

Jumlah kedua jari-jari (r1+r2) nilainya sama dengan jarak antara kedua pusat lingkaran (d).

Jadinya, d = r1+r2

Artinya, kalau melihat gambar kedudukan kedua lingkaran di atas, maka posisi kedua lingkaran bersinggungan di luar (C).

Baca Juga: Cara Mencari Titik Pusat Lingkaran dan Pengertiannya

Topik Soal 2: Suku Banyak

Suku banyak biasa elo kenal sebagai polinomial. Elo bisa flashback dikit materinya di sini, ya.

Pada bab suku banyak, materi yang elo pelajari antara lain tentang akar-akar suku banyak, pembagian suku banyak, teorema faktor, teorema sisa, sampai pembagian istimewa.

Di bawah ini, ada tiga contoh soal PAT semester 2 Matematika IPA kelas 11 tentang suku banyak. Materinya tentang apa? Random, dong. Langsung aja, yuk, coba kerjakan!

Jawaban: A

Pembahasan

Jika polinomial f(x) dibagi (ax+b), maka sisa pembagiannya adalah f(-b/a)

Pada x+2, a = 1, b = 2

Kalau disubstitusikan ke dalam P(x) dengan sisa 3, maka:

P(-21)= 3

P(-2) = 3

Pada x+1, a = 1, b = 1

Kalau disubstitusikan ke dalam P(x) dengan sisa 1, maka:

P(-11)= 1

P(-1) = 1

Pada Q(x), langsung aja kita substitusikan karena punya pembagi yang sama, yaitu x+2 dan x+1. Maka,

Q(-2) = 4

Q(-1) = 1

Diketahui, R(x) = P(x).Q(x)

Bentuk ini bisa kita ubah dengan:

R(-2) = P(-2) . Q(-2), dan R(-1) = P(-1) . Q(-1)

Kita hitung satu per satu.

R(-2) = P(-2) . Q(-2)

R(-2) = 3 x 4

R(-2) = 12.

R(-1) = P(-1) . Q(-1) 

R(-1) = 1 x 1

R(-1) = 1

Yang ditanyakan adalah sisa pembagian R(x) dibagi x2+3x+2

Jika polinomial f(x) dibagi (x-a)(x-b), maka sisa pembagiannya adalah px+q, di mana f(a) = pa+q dan f(b) = pb+q.

Dengan bentuk umum pembagian suku banyak: 

F(x) = P(x).H(x) + S(x)

Keterangan:

F(x) = Suku banyak
P(X) = Pembagi
H(x) = Hasil bagi
S(x) = Sisa

Elo bisa flashback lagi pembagian polinomial di artikel Pembagian Pada Suku Banyak? Itu Mah Gampang!

Sekarang, kita terapkan bentuk umum itu pada R(x) yang dibagi x2+3x+2, jadinya:

R(x) = (x2+3x+2) . H(x) +  (px+q)

Kalau R(a) = pa + q, dan R(b) = pb +q, tinggal kita substitusikan aja dengan substitusi R(x) yang udah kita hitung sebelumnya.

• R(-2) = 12

-2p + q = 12

• R(-1) = 1

-p + q = 1

Buat nyari sisa pembagian, yaitu (px+q), kita nyari nilai p dan q. Kurangi dua persamaan di atas, menjadi:

• R(-2) – R(-1) = 12 – 1

(-2p + q) – (-p + q) = 11

-p = 11

p = -11

Kita tinggal nyari q. Substitusikan p ke dalam salah satu persamaan R(x). Elo bisa ambil dari R(-1).

• R(-1) = 1

-p + q = 1

-(-11) + q = 1

11 + q = 1

q = -10.

Bentuk sisa pembagian adalah px + q, maka:

Sisa pembagian = -11x-10.

Jawabannya adalah A.

Baca Juga: Penjumlahan dan Pembagian Polinomial – Materi Matematika Kelas 11

2. Jika x + 2 merupakan faktor dari P(x)=x3+ax2+x-6, maka faktor lain dari P(x) adalah ….

A. x+1

B. x+3

C. x+4

D. x-4

E. x-3

Jawaban: B

Pembahasan

Dalam hubungan teorema sisa dan teorema faktor, jika bentuk faktornya adalah (x-h), maka sisa pembagiannya nol (0), atau polinomial P(x) habis dibagi oleh (x-h). P(x) = 0.

Kalau bentuk (x-h) disesuaikan dengan faktor pada soal (x+2), maka h = -2.

Yang ditanyakan adalah faktor lain dari P(x). Buat mencari faktor lain, kita bagi suku banyaknya. Metode pembagian suku banyak yang bisa elo pakai adalah metode Horner bersusun.

Kalau elo lupa-lupa ingat sama metode Horner, elo bisa pelajari lagi di Metode Horner dan Contoh Soalnya – Materi Matematika Kelas 11.

Buat menggunakan metode Horner bersusun, tentukan dulu koefisien masing-masing x pada persamaan P(x).

Kita hitung pembagian suku banyak dengan metode Horner bersusun. Hasil pembagiannya 

dengan tinggal dibagi dengan (x-h), atau x= -2, jadinya seperti di bawah ini.

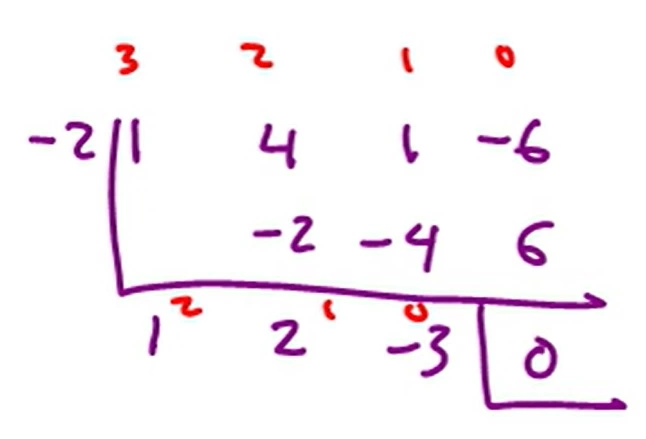
Berdasarkan perhitungan di atas, karena dibagi, maka pangkatnya turun dari pangkat tiga menjadi pangkat dua, dengan:

Di opsi jawaban, nggak ada pilihan jawaban (x-1).

Jadi, jawabannya adalah (x+3). (B).

Baca Juga: Teorema Sisa dan Teorema Faktor – Materi Matematika Kelas 11

*****

Yuk, Belajar PAT Bareng Zenius!

Akhirnya, elo udah belajar contoh soal PAT Semester 2 Matematika IPA kelas 11, beserta pembahasannya. Buat elo yang mau ngerjain lebih banyak lagi contoh soal PAT Semester 2 Matematika IPA kelas 11, Zenius udah menyediakan berbagai latihan soal khusus buat elo.

Elo tinggal klik gambar di bawah ini. Pastikan elo udah punya akun Zenius, ya.

Elo juga bisa review lagi materi Matematika IPA kelas 11 semester genap. Langsung meluncur ke link sebelah, yes>>> Materi Matematika IPA kelas 11 Semester 2

Sekian dari gue. Semoga pembahasan contoh soal PAT semester 2 Matematika IPA kelas 11 di atas bisa membantu elo lebih siap dalam menghadapi PAT.

Beli sate di dekat rumah Anya. Semangat PAT, gue tunggu kabar baiknya!