Halo Sobat Zenius! Kali ini, gue mau bahas tentang persamaan kuadrat lagi, nih. Ya, seperti yang tertera pada judul, gue akan bahas rumus diskriminan, dari persamaan kuadrat, pengertian diskriminan, dan contoh soal beserta pembahasannya..
Kalau pada artikel-artikel sebelumnya, gue sudah pernah bahas tentang pemfaktoran, kuadrat sempurna, dan rumus ABC untuk mencari akar dari persamaan kuadrat. Jadi, ini merupakan materi lanjutan dari materi-materi sebelumnya.
Daftar Isi
Apa yang Dimaksud dengan Diskriminan?
Diskriminan adalah suatu nilai yang menjadi penentu sifat-sifat dari akar suatu persamaan kuadrat. Jadi, jenis akar dari persamaan kuadrat dapat ditentukan dengan cara mengetahui nilai diskriminan atau dapat dinotasikan dengan D, guys.
Rumus Diskriminan
Untuk mengetahui akar-akar dari persamaan kuadrat , Sobat Zen bisa menggunakan rumus ABC.
Nah, Sobat Zen, rumus diskriminan itu ternyata dapat ditemukan dalam rumus ABC, lho. Rumus diskriminan adalah seperti di bawah ini, dengan a, b, dan c sebagai konstanta yang bersesuaian dengan persamaan kuadrat.
D = b² – 4ac
Lalu, rumus ABC dapat juga menjadi seperti ini. Sobat Zenius tahu, gak? Rumus ini dapat dipakai jika yang diketahui adalah nilai diskriminannya, lho.
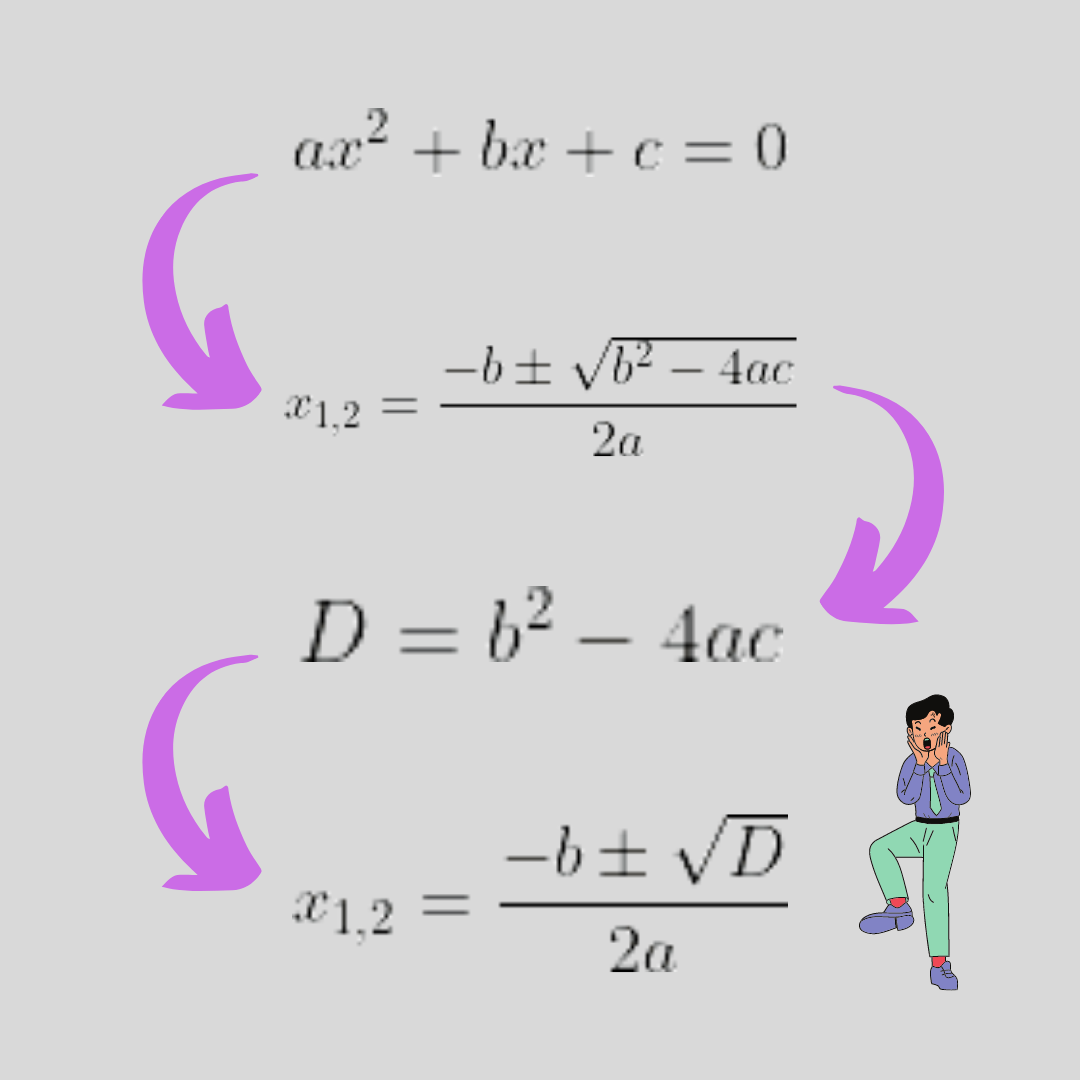
Diskriminan dalam rumus ABC menentukan jenis dari akar-akar persamaan kuadrat berupa bilangan real atau bilangan tidak real. Jenis akar-akar persamaan kuadrat adalah sebagai berikut, guys.
Jika D < 0 atau nilai diskriminan kurang dari 0, maka akar-akarnya adalah tidak real atau imajiner. .
Jika D > 0 atau nilai diskriminan lebih dari 0, maka akar-akarnya adalah real () dan berbeda atau berlainan (
).
Jika D = 0 atau nilai diskriminan sama dengan, maka akar-akarnya adalah real () dan sama atau kembar (
).
Sebelum lanjut bahas materi diskriminan persamaan kuadrat ini, yuk download dulu aplikasi Zenius-nya. Elo bisa dapet ribuan materi soal yang lebih lengkap beserta latihan soalnya. Ada beberapa fitur gratis juga lho yang bisa elo manfaatin. Klik gambar di bawah ya, sesuai dengan device yang elo pake!
Download Aplikasi Zenius
Tingkatin hasil belajar lewat kumpulan video materi dan ribuan contoh soal di Zenius. Maksimaln persiapanmu sekarang juga!
Contoh Soal dan Pembahasan
Soal 1
Dari persamaan kuadrat , tentukan jenis akar persamaan kuadratnya!
Jawab:
D = b² – 4ac
D =
D = 25 – 24
D = 1
Diketahui nilai diskriminan adalah 1 atau D = 1 > 0, maka persamaan kuadrat tersebut memiliki akar-akar real dan berlainan.
Soal 2
Persamaan kuadrat memiliki akar-akar yang berlainan, maka tentukan nilai b!
Jawab:
D =
D = b² + 4b + 4 -16
D = b² + 4b – 12
b² + 4b – 12 > 0
(b + 6)(b – 2) > 0
Jadi, b < -6 atau b > 2
Sampai di sini saja materi diskriminan persamaan kuadrat kita kali ini. Eits, materi habis bukan berarti Sobat Zenius berhenti belajar, ya. Terus berlatih mengerjakan soal-soal untuk memantapkan penguasaan materi Sobat Zenius.
Kalo elo mau ganti cara belajar jadi yang lebih efektif, coba aja langganan paket belajar Zenius Aktiva Sekolah. Elo akan dibimbing para Zen Tutor yang asik, perdalam materi lewat video pembahasan, trus bisa evaluasi lewat try out deh. Klik gambar di bawah buat info selanjutnya ya!
Jangan lupa untuk ikuti keseruan Zenius di YouTube juga, ya! Sampai jumpa!
Baca Juga Artikel Lainnya
Originally Published: September 18, 2021
Updated By: Arum Kusuma Dewi
Share Your Comment!