Halo Sobat Zenius, elo pasti familiar sama yang namanya limit dalam mata pelajaran matematika, kan?

Limit itu apa, sih? Limit bisa diartikan sebagai sebuah nilai yang mendekati nilai fungsi. Maksudnya gimana, tuh? Jadi, limit ini biasanya digunakan buat menyatakan suatu nilai ketika nilai tersebut mendekati nilai tertentu.

Dalam menghitung fungsi limit, elo bisa menggunakan beberapa metode. Salah satunya yaitu menggunakan dalil L’Hopital atau yang biasa disebut dengan aturan L’Hopital. Nantinya elo bakal ketemu sama materi ini di pelajaran matematika peminatan SMA kelas 12.

Di artikel kali ini, gue mau ngebahas mulai dari apa itu L’Hopital, siapa itu L’Hopital yang menciptakan rumusnya, hingga mengapa metode ini disebut teorema L’Hopital?

Supaya nggak bingung dan penasaran lagi, langsung saja kita masuk ke pembahasannya, yuk!

Daftar Isi

Apa itu Dalil L’Hopital?

Seperti biasa, sebelum kita memulai pembahasan lebih jauh, gue mau ngajak elo buat kenalan dulu sama apa itu L’Hopital?

Ternyata, nama dalil L’Hopital ini diambil dari nama penemunya, yaitu Guillaume de L’Hôpital. Siapa itu L’Hopital? Ia merupakan seorang matematikawan asal Prancis yang juga dikenal dengan nama Guillaume-François-Antoine Marquis de l’Hôpital dan lahir pada tahun 1661.

Nah, aturan L’Hopital limit boleh dipakai jika untuk menghitung dan menemukan fungsi limit yang hasilnya tak tentu, misalnya kayak limit yang hasilnya berupa 0/0 atau ∞/∞. Hasil tersebut juga yang menjadi alasan mengapa disebut Teorema L’Hopital.

Oh iya, dalil L’Hopital ini berlaku buat fungsi trigonometri maupun fungsi aljabar, ya. Makanya penting buat elo memahami terlebih dahulu gimana caranya mencari turunan dari sebuah fungsi, baik itu fungsi trigonometri maupun fungsi aljabar. Nggak cuma ini aja, kamu juga bisa cara mencari limit akar menggunakan dalil L’Hopital.

Menghitung Limit Menggunakan Formula Dalil L’Hopital

Tadi kan kita udah kenalan nih sama apa itu aturan L’Hopital. Terus, kayak apa sih bunyinya rumus aturan L’Hopital ini?

Aturan L’Hopital berbunyi, misalkan f(x) dan g(x) fungsi yang terturunkan pada interval terbuka I.

rumus limit l hopital — Menghitung limit menggunakan dalil L’Hopital. (Arsip Zenius)

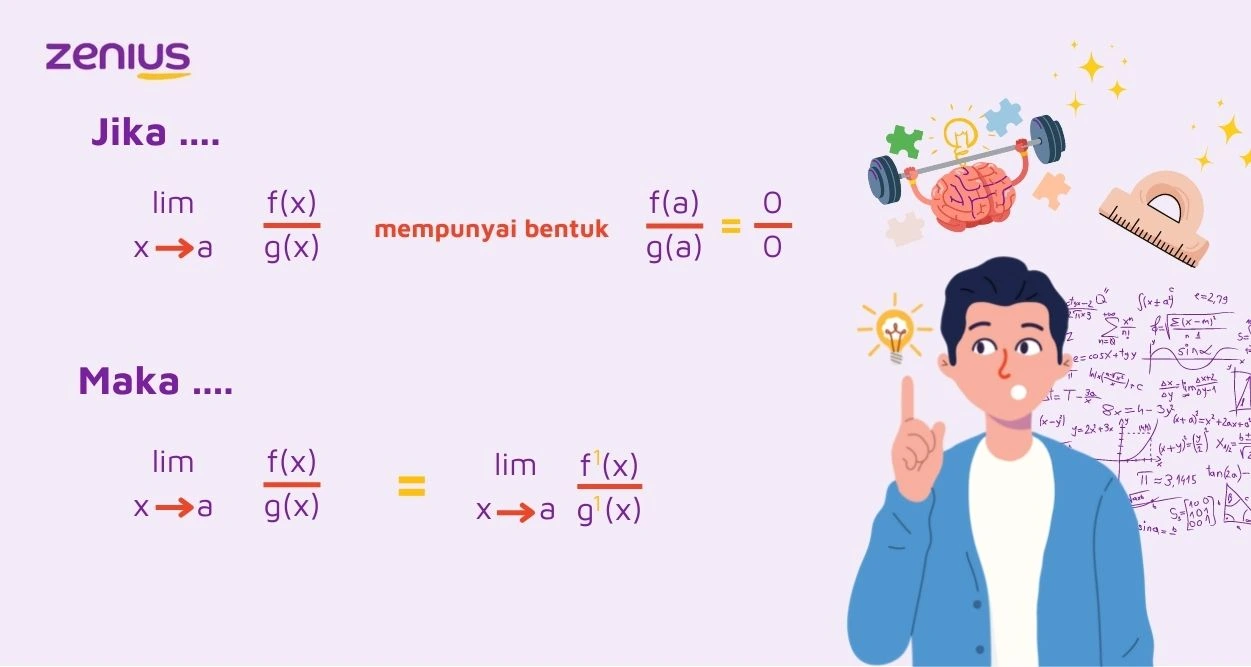
Masih bingung sampai sini? Oke, gue coba jelasin pelan-pelan, ya.

Aturan L’Hopital memberi tahu kalau misalnya elo punya limit tak tentu dengan hasil 0/0 atau ∞/∞, elo bisa menyelesaikan limit tersebut dengan menurunkan si pembilang dan penyebut dari fungsi limitnya. Setelah itu, nanti substitusi dari nilai si x ketika dimasukkan ke dalam fungsi yang udah diturunkan, bisa memperoleh nilai limit yang elo inginkan.

Seperti yang gue bilang tadi, karena rumus ini berbunyi fungsi yang terturunkan pada interval terbuka I, maka untuk menghitung limit menggunakan aturan L’Hopital, elo harus menurunkan fungsinya terlebih dahulu.

Inilah sebabnya kenapa bisa kita lihat $Mengenal Dalil L'Hopital dan Contoh Soalnya 385$ , di mana $Mengenal Dalil L'Hopital dan Contoh Soalnya 386$ merupakan hasil turunan dari f(x). Begitu pula dengan $Mengenal Dalil L'Hopital dan Contoh Soalnya 387$ yang merupakan turunan dari g(x).

Karena di sini kita mau mencari $Mengenal Dalil L'Hopital dan Contoh Soalnya 388$ , maka nilai $Mengenal Dalil L'Hopital dan Contoh Soalnya 389$ atau nilai turunan a-nya harus ada, supaya kita bisa memenuhi syarat fungsi yang terturunkan buat menggunakan formula dari aturan L’Hopital. Kalau ketika diturunkan nggak ada nilainya, maka kita nggak bisa menggunakan aturan L’Hopital ini.

Sudah mulai tercerahkan belum sampai sini, Sobat Zenius? Kalau masih bingung, tenang, gue bakal coba menggambarkan rumusnya pakai sebuah contoh supaya elo bisa lebih kebayang dan lebih mudah lagi memahaminya, ya.

Misalkan di sini kita punya fungsi $Mengenal Dalil L'Hopital dan Contoh Soalnya 390$ . Kemudian, kalau x-nya kita ganti jadi 0, maka fungsi limitnya akan menghasilkan $Mengenal Dalil L'Hopital dan Contoh Soalnya 391$ menjadi $Mengenal Dalil L'Hopital dan Contoh Soalnya 392$ .

Karena bentuknya memenuhi syarat dari aturan L’Hopital, maka perhitungannya jadi kayak gini:

$Mengenal Dalil L'Hopital dan Contoh Soalnya 393$

Eh, bentar! Kok bisa kayak gitu jadinya? Supaya nggak bingung kenapa bisa jadi $Mengenal Dalil L'Hopital dan Contoh Soalnya 394$ , itu merupakan hasil dari turunan $Mengenal Dalil L'Hopital dan Contoh Soalnya 395$ , ya. Kembali gue ingatkan kalau syarat menggunakan aturan L’Hopital yaitu fungsi yang terturunkan. Makanya di sini, kita menurunkan fungsi $Mengenal Dalil L'Hopital dan Contoh Soalnya 395$ yang menjadi $Mengenal Dalil L'Hopital dan Contoh Soalnya 394$ .

Setelah turunannya sudah ketemu, selanjutnya apa yang kita lakukan, nih? Elo tinggal memasukkan nilai x-nya aja ke dalam rumusnya. Karena nilai x menuju 0, jadi perhitungan limitnya bakal jadi kayak gini ….

$Mengenal Dalil L'Hopital dan Contoh Soalnya 398$

Nilai dari $Mengenal Dalil L'Hopital dan Contoh Soalnya 399$ ,

Sehingga hasil limitnya adalah 1.

Ternyata nggak sulit kan setelah melihat contohnya? 😀

Contoh Soal L’Hopital

Melihat contohnya di atas, gimana menurut elo nih Sobat Zenius? Kira-kira, menghitung fungsi limit menggunakan dalil L’Hopital ini gampang atau susah? Nah, supaya bisa jawabnya, langsung kita buktikan dengan mengerjakan contoh contoh soal teorema L’Hopital pada aplikasi turunan, yuk!

Hitunglah limit fungsi berikut ini dengan menggunakan aturan L’Hopital.

Soal 1:

$Mengenal Dalil L'Hopital dan Contoh Soalnya 400$

a. -4

b. -2

c. 0

d. 2

e. 4

Pembahasan 1:

Pertama, untuk mencari nilai limitnya kita substitusi nilai x = 0 ke fungsi $Mengenal Dalil L'Hopital dan Contoh Soalnya 401$ , yaitu menjadi $Mengenal Dalil L'Hopital dan Contoh Soalnya 402$ .

Karena pada saat kita substitusi nilai x = 0 menghasilkan nilai limit bentuk tak tentu yaitu $Mengenal Dalil L'Hopital dan Contoh Soalnya 391$ , maka kita gunakan dalil L’Hopital untuk mencari nilai limitnya. Sehingga ….

$Mengenal Dalil L'Hopital dan Contoh Soalnya 404$

$Mengenal Dalil L'Hopital dan Contoh Soalnya 405$

$Mengenal Dalil L'Hopital dan Contoh Soalnya 406$

= 4.

Jadi, jawaban yang paling tepat adalah e.

Soal 2:

$Mengenal Dalil L'Hopital dan Contoh Soalnya 407$

a. -2

b. $Mengenal Dalil L'Hopital dan Contoh Soalnya 408$

c. $Mengenal Dalil L'Hopital dan Contoh Soalnya 409$

d. $Mengenal Dalil L'Hopital dan Contoh Soalnya 410$

e. 0

Pembahasan 2:

Pertama, untuk mencari nilai limitnya kita substitusi nilai $Mengenal Dalil L'Hopital dan Contoh Soalnya 411$ , yaitu menjadi $Mengenal Dalil L'Hopital dan Contoh Soalnya 412$ .

Karena nilai limitnya adalah $Mengenal Dalil L'Hopital dan Contoh Soalnya 391$ , maka kita bisa menggunakan dalil L’Hôpital sebagai berikut:

Untuk mendapatkan turunan dari cos2x, kita gunakan aturan rantai yaitu turunannya adalah -2sin2x. Sehingga:

$Mengenal Dalil L'Hopital dan Contoh Soalnya 414$

$Mengenal Dalil L'Hopital dan Contoh Soalnya 415$

$Mengenal Dalil L'Hopital dan Contoh Soalnya 416$

$Mengenal Dalil L'Hopital dan Contoh Soalnya 417$

$Mengenal Dalil L'Hopital dan Contoh Soalnya 418$

$Mengenal Dalil L'Hopital dan Contoh Soalnya 419$

Jadi, jawaban yang benar adalah b.

Soal 3:

$Mengenal Dalil L'Hopital dan Contoh Soalnya 420$

a. $Mengenal Dalil L'Hopital dan Contoh Soalnya 421$

b. $Mengenal Dalil L'Hopital dan Contoh Soalnya 422$

c. $Mengenal Dalil L'Hopital dan Contoh Soalnya 423$

d. 1

e. 3

Pembahasan 3:

Pertama, untuk mencari nilai limitnya kita substitusi nilai x = 3 ke fungsi $Mengenal Dalil L'Hopital dan Contoh Soalnya 424$ , yaitu menjadi $Mengenal Dalil L'Hopital dan Contoh Soalnya 425$ .

Karena nilai limitnya adalah $Mengenal Dalil L'Hopital dan Contoh Soalnya 391$ , maka kita bisa menggunakan dalil L’Hôpital sebagai berikut:

Untuk mendapatkan turunan dari sin(3x – 9), kita gunakan aturan rantai yaitu turunannya adalah 3 cos(3x – 9). Sehingga:

$Mengenal Dalil L'Hopital dan Contoh Soalnya 427$

$Mengenal Dalil L'Hopital dan Contoh Soalnya 428$

$Mengenal Dalil L'Hopital dan Contoh Soalnya 429$

$Mengenal Dalil L'Hopital dan Contoh Soalnya 430$

$Mengenal Dalil L'Hopital dan Contoh Soalnya 431$

Jadi, jawaban yang paling tepat adalah c.

Semoga penjelasan dan contoh soal tadi bisa membantu mencerahkan elo tentang materi ini ya, Sobat Zenius.

Kalau misalnya elo masih penasaran sama materi ini dan pengen mendalami materinya supaya makin khatam lagi, elo bisa banget menonton video materi belajar Zenius lewat aplikasi maupun website Zenius dengan klik banner di bawah ini, ya!

Mengenal Dalil L'Hopital dan Contoh Soalnya 432

Kalau Sobat Zenius ingin memperdalam wawasan di materi lainnya, kalian bisa coba dengan berlangganan paket belajar Zenius! Klik gambar di bawah ini ya, dijamin belajar kalian juga bakal makin seru!