Materi Trigonometri Kelas 10 – Rumus Sin Cos Tan & Pembahasannya

Hi, Sobat Zenius! Ketemu lagi nih. Kali ini, gue akan mencoba membahas materi trigonometri kelas 10. Tapi sebelumnya, elo udah bisa menghitung rumus sin cos tan belum nih? Kalau belum, tenang aja karena gue juga bakal bahas itu semuanya di artikel ini. Simak terus, ya!

Nggak perlu buru-buru ke materi trigonometri sin cos tan ya. Elo harus perlu paham konsep dasar segitiga dulu, apalagi segitiga siku-siku. Elo inget nggak, segitiga siku-siku punya tiga sisi yaitu depan, samping, dan miring. Oh iya, jumlah dari ketiga sudut itu hasilnya 180⁰.

Elo juga perlu tahu nih, kalau konsep materi tentang trigonometri itu berkaitan banget sama ilmu populer seperti astronomi, navigasi, dan geografi. Di bidang-bidang teknis itu, elo bakal banyak banget menggunakan rumus sinus cosinus tangen atau yang biasa disebut sin cos tan.

Belajar rumus sin cos tan tuh perlu banget banyak latihan, lho. Yuk temuin banyak latihan soal tentang materi ini di aplikasi Zenius. BTW, buat Sobat Zenius yang belum download aplikasi Zenius, yuk download apps-nya sekarang dengan klik banner di bawah ini. Pilih sesuai device yang elo gunakan ya!

Pengertian Trigonometri

Trigonometri berasal dari bahasa Yunani, yaitu trigonon yang memiliki arti “tiga sudut” dan metron yang memiliki arti “mengukur”. Trigonometri adalah salah satu cabang matematika tentang hubungan antar sudut dan sisi pada segitiga.

Nah, rumus trigonometri dipakai untuk menghitung sudut di segitiga. Sobat Zenius, nantinya bakal kenalan sama sin, cos, tan dan lainnya. Tapi elo mending belajar kesebangunan dulu, yuk!

Trigonometri termasuk dalam pembahasan ragam rumus matematika. Untuk mempelajari ragam rumus lain, kamu bisa kunjungi artikel berikut: Kumpulan Rumus Matematika Lengkap dengan Keterangannya.

Kesebangunan dan Rumus Trigonometri Dasar

Dua segitiga meskipun sisinya berbeda panjang mungkin sebangun, lho. Coba deh elo cek dua segitiga berbeda di bawah ini, diperhatikan juga ya hasil perbandingannya.

Kok bisa sama sih perbandingannya? Itu yang dinamakan sebangun atau bisa dibilang kedua segitiga memiliki sudut yang sama besar. Nggak heran deh makanya perbandingannya bisa sama. 

Catatan: pada segitiga yang sebangun, perbandingan sisinya sama. Lalu, muncul istilah untuk perbandingan sudut yang bernama sin, cos, dan tan.

Rumus  sin, cos dan tan trigonometri, bisa elo lihat langsung di bawah ini.

Jadi, Sin didapat dari sisi depan per sisi miring, Cos didapat dari sisi samping per sisi miring, dan Tan didapat dari sisi depan per sisi samping. Untuk Cosec, sec, dan cot kalau elo perhatikan rumus di atas, itu cuma kebalikannya dari sin cos tan.

Dari mana sih, asalnya rumus trigonometri? Pelajari juga bagaimana cara membuktikan rumus trigonometri di artikel berikut: Konsep Trigonometri & Pembuktiannya.

Sudut Istimewa

Pada segitiga-segitiga sulit diketahui angka yang pasti. Namun, terdapat segitiga-segitiga yang istimewa. Maksudnya istimewa nih apa? Segitiga istimewa ini tepat banget angka-angkanya. Bisa dibilang sebagai sudut istimewa trigonometri.

Segitiga istimewa ini dibangun dari sesuatu yang kita sudah tahu pasti, contohnya segitiga sama sisi dan persegi. Mengapa kedua bangun tersebut? Karena kita sudah tahu jumlah sudut pada segitiga sama sisi adalah 180 derajat dan pada persegi masing-masing sudutnya 90 derajat.

Jadi, jika dihitung maka nilai-nilainya seperti pada tabel berikut.

Sudut Berelasi pada Kuadran

Pertama elo harus paham kuadran dulu nih. Kuadran adalah setiap dari empat bagian suatu bidang datar yang terbagi oleh suatu sumbu silang. Sumbu silang tersebut adalah sumbu x dan sumbu y.

Pada prinsipnya, nilai sin akan positif jika y-nya positif. Jika x-nya positif, nilai cos akan positif. Nilai tan akan positif jika x dan y sama-sama positif atau negatif. Terakhir, nilai k akan selalu positif.

Nah, Sobat Zenius, berdasarkan yang disebutkan di atas, maka nilai pada kuadran adalah sebagai berikut.

• Kuadran I (0° − 90°) = semua positif.
• Kuadran II (90° − 180°) = sin positif.
• Kuadran III (180° − 270°) = tan positif.
• Kuadran IV (270° − 360°) = cos positif.

Lebih mudahnya, perhatikan gambar di bawah.

Elo nggak perlu kok menghafal satu per satu. Elo cukup perhatikan kalau rumus-rumus di atas memiliki pola yang sama. Terutama sudut relasi yang dipakai dan tanda untuk setiap kuadran.

Untuk relasi (90° ± α°) atau (270° ± α°)

• sin → cos
• cos → sin
• tan → cot

Untuk relasi (180° ± α°) atau (360° ± α°)

• sin = sin
• cos = cos
• tan = tan

Mungkin susah banget ya untuk ngerti cara menghitung trigonometri kalau cuma dari baca. Kalau mau lebih jelas lagi elo bisa lihat video pembahasanya yang ini ya!

Sudut Negatif

Elo tahu nggak nih, sudut positif adalah sudut yang arah putarannya berlawanan dengan jarum jam, sedangkan sudut negatif adalah sudut yang arah putarannya searah jarum jam. Tapi, sudut negatif bisa juga didapat dari rumus berikut.

• cosec (-α) = -cosec α
• sec (-α) = sec α
• cot (-α) = -cot α

Sudut Lebih dari 360 Derajat

Kalau sudutnya lebih dari 360 derajat, gimana dong? Begini nih caranya, perhatikan gambar berikut, ya!

Identitas Trigonometri

Sobat Zenius sudah tahu rumus pythagoras, dong? Ya, kan? Dinget-inget lagi yuk. Soalnya untuk mengetahui identitas trigonometri perlu pengetahuan konsep tentang dasar trigonometri dan pythagoras. Nah, jelasnya cobaperhatikan gambar berikut untuk membuktikan identitas-identitas dari trigonometri.

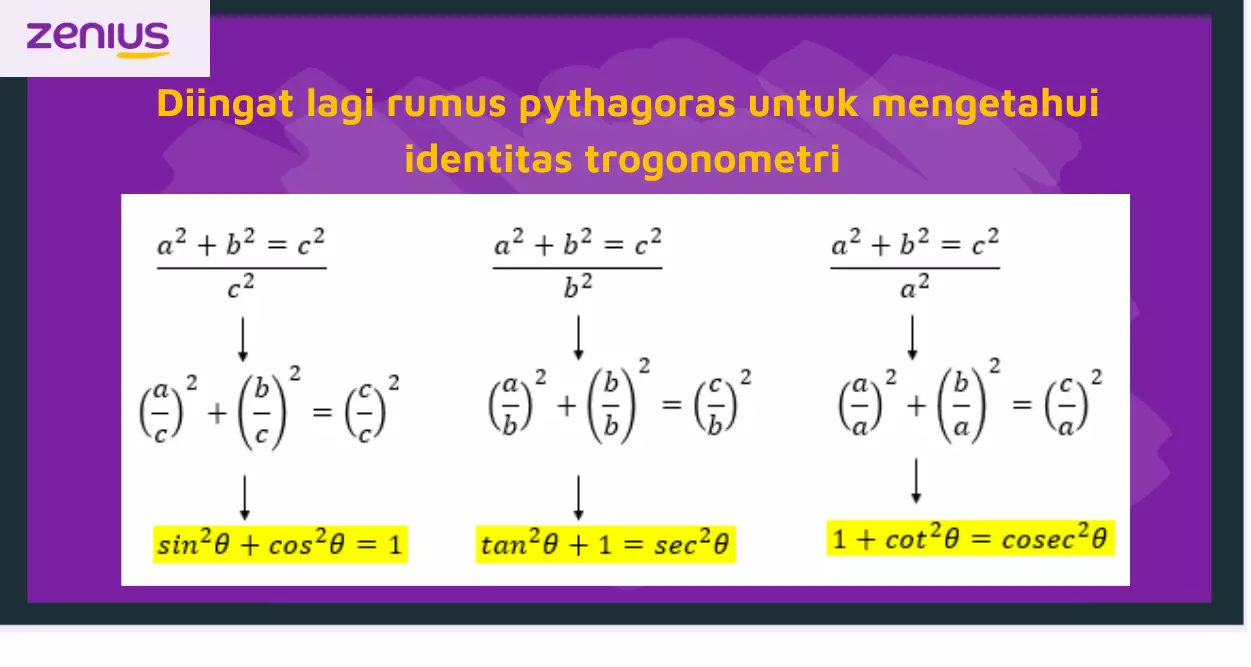
Bingung nggak nih? Kok bisa berubah jadi sin, cos dan tan? Coba deh elo cek rumus dasar trigonometri sin cos tan dulu. Untuk jelasnya bisa elo lihat di sini!

Kamu bisa mempelajari lagi materi khusus rumus-rumus trigonometri yang meliputi identitas, jumlah/selisih sudut, sudut ganda, dan sudut paruh di artikel berikut: Rumus-Rumus Trigonometri.

Persamaan Trigonometri

Persamaan trigonometri memiliki prinsip yang sama dengan persamaan linear atau kuadrat. Elo masih inget nggak? Bedanya kalau persamaan trigonometri hasilnya berupa besar sudut. Persamaan trigonometri adalah persamaan yang berisi fungsi trigonometri dari sudut yang belum diketahui nilainya.

Elo mungkin banget lho menemukan nilai sudut yang lebih dari satu. Kok bisa? Hal ini, dapat disebabkan oleh grafik fungsi trigonometri karena terdapat nilai yang sama di beberapa sudut.

Pelajari juga materi Grafik Fungsi Trigonometri dan Cara Menggambarnya link berikut: Cara Menggambar Grafik Fungsi Trigonometri dan Persamaannya.

Aturan Sinus & Aturan Cosinus

Aturan Sinus

Aturan sinus memiliki peran dalam hubungan perbandingan antara setiap sisi dan sudut sinus memiliki nilai yang sama.

a = panjang sisi a

b = panjang sisi b

c = panjang sisi c

A = besar sudut di depan sisi a

B = besar sudut di depan sisi b

C = besar sudut di depan sisi c

Nah, dari aturan sinus ini elo bisa tahu bahwa sudut terbesar tuh berhadap-hadapan dengan sisi terpanjang. Begitu juga dengan sudut terkecil dengan sisi terpendek. Ditunjukkan dengan sudut A berhadapan dengan sisi a dan seterusnya.

Oh iya, kalau elo lihat gambar di atas, mulanya segitiganya nggak punya sisi t. Nah, itu ada sebagai garis pembantu agar segitiganya bisa berbentuk siku-siku. 

Kok harus siku-siku? Kan elo perlu cari Sin-nya tuh. Rumus Sin perlu sisi depan dan sisi miring. Sisi t itu kemudian yang jadi sisi depannya. Proses selanjutnya bisa elo amati di gambar.

Aturan Cosinus

Aturan cosinus adalah adalah aturan yang memberikan hubungan yang berlaku antara panjang sisi-sisi dan salah satu sudut cosinus dalam segitiga.

a = panjang sisi a

b = panjang sisi b

c = panjang sisi c

A = besar sudut di depan sisi a

B = besar sudut di depan sisi b

C = besar sudut di depan sisi c

Bagaimana Sobat Zenius, sampai di sini sudah paham kan tentang rumus sin cos tan? Biar makin paham, elo juga bisa lihat penjelasan lengkapnya dalam versi video lho. Klik banner di bawah ini ya!

Nggak lupa untuk coba contoh soal trigonometri sin cos tan di bawah ini ya untuk ukur kemampuan elo sampai mana. Tenang, bakal ada pembahasannya juga kok.

Contoh Soal dan Pembahasan

Soal 1

Diketahui , tentukan nilai tan A!

Jawab:

Elo bisa mulai dari bikin segitiga. Diinget juga Sin itu sisi depan dibagi sisi miring. Nah, tinggal dimasukin ke segitiganya. Untuk hitung Tan kan elo perlu sisi samping tuh, sedangkan elo belum tahu berapa. Bisa elo hitung pake pythagoras tuh. Nanti berbentuk segitiga gini nih:

Dari ilustrasi segitiga yang digambarkan karena mengetahui nilai sin A, maka nilai tan A adalah

Soal 2

Diketahui sudut sin A < 0, berada di kuadran berapa sudut tersebut?

Jawab:

Ingat-ingat kembali sudut-sudut pada kuadran. Kalau kurang dari 0 berarti masuk bilangan negatif ya. Nah, Sin akan bernilai negatif jika sudutnya berada pada kuadran III dan kuadran IV.

Soal 3

Pada sudut lebih dari 360 derajat, berapakah nilai sin 960⁰?

Jawab:

Pertama, tentukan kuadrannya.

sin 960⁰ = sin (720⁰ + 240⁰)

sin 960⁰ = sin 240⁰ (kuadran III)

Selanjutnya, tentukan nilai sin. 

sin 960⁰ = sin (180⁰ + 60⁰)

sin 960⁰ = sin (2 x 90⁰ + 60⁰)

sin 960⁰ = – sin 60⁰ = .

Untuk permasalahan atau persoalan lainnya dapat Sobat Zenius lihat di sini.

Udah selesai deh belajar materi trigonometri sin cos tan. Lumayan susah kan? Tapi, nggak boleh gampang nyerah ya, elo pasti bisa menguasai materi trigonometri kelas 10 dari rumus trigonometri, sudut istimewa trigonometri dan nggak lupa rumus sinus cosinus tangen. Yang penting elo banyak latihan dan belajar ya!

Khusus buat sobat Zenius yang ingin meningkatkan nilai rapor, sekaligus nambah pemahaman semua materi pelajaran di sekolah. Elo bisa berlangganan paket belajar Zenius.

Di paket belajar ini, elo bakal diberikan akses ke ribuan video belajar premium, dibimbing langsung sampai paham sama tutor Zenius di Live Class, ikut Try Out buat mengukur kemampuan jawab soal, sampai latihan soal biar elo makin jago menghadapi segala jenis soal ujian. Yuk, cek info lengkapnya dengan klik banner di bawah ini sekarang!

Jangan lupa untuk terus ikuti keseruan lainnya dari Zenius di YouTube! Sampai jumpa!

Sering nemu soal matematika yang sulit elo jawab? Santai aja boy, nih kenalin ZenBot, temen 24 jam yang siap bantu kamu cari solusi dari masalah matematika!

Untuk menjawab soal-soal tentang bilangan dan soal matematika lainnya, elo juga bisa manfaatkan fitur dari ZenBot, lho! Tanyain soal yang elo gak bisa jawab mulai dari download aplikasi Zenius untuk OS atau Android sekarang juga!

Originally published: September 18, 2021
Updated by: Silvia Dwi & Rizaldi Abror