Halo Sobat Zenius, di artikel ini aku mau ngajak kamu buat belajar tentang rumus luas segitiga siku siku, mulai dari pengertiannya hingga contoh soal dan pembahasannya. Yuk baca artikel ini sampai selesai!
Sebelum lebih jauh, kamu tentu sudah tahu kalau ternyata segitiga itu ada beragam jenisnya, salah satunya adalah segitiga siku siku. Segitiga jenis ini memiliki satu sisi yang membentuk sudut tegak lurus 90°. Sedangkan sisi lainnya ada yang miring dan itulah yang paling panjang ukurannya. Oke deh, langsung aja yuk kita bahas lebih detail!
Daftar Isi
Apa Itu Segitiga Siku Siku?
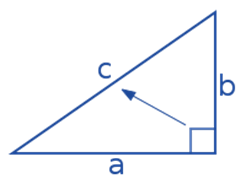
Di atas udah aku singgung sedikit, kalau segitiga siku siku adalah salah satu jenis segitiga yang salah satu sisinya tegak lurus dan membentuk sudut 90°. Kamu bisa lihat gambar bangunnya di bawah ini:
Sisi yang c adalah sisi miring atau hipotenusa. Nah, sisi yang tegak lurus adalah sisi a dan b yang disebut alas dan tinggi. Supaya kamu bisa lebih mudah dalam memahami seperti apa sih segitiga siku siku itu, bisa dicek dari ketiga sifatnya berikut ini:
- Segitiga siku siku memiliki dua sisi yang saling tegak lurus.
- Segitiga siku siku memiliki satu sisi miring dan salah satu sudutnya adalah sudut siku siku atau 90°.
- Segitiga siku siku tidak memiliki simetri putar dan simetri lipat.
Nah, kalau kamu udah paham sama ketiga sifat di atas, berarti udah gak bingung lagi dong membedakan segitiga siku siku dengan segitiga lainnya.
Sebelum lebih jauh, buat kamu yang belum punya aplikasi Zenius, yuk download app-nya dengan klik banner di bawah ini!
Download Aplikasi Zenius
Tingkatin hasil belajar lewat kumpulan video materi dan ribuan contoh soal di Zenius. Maksimalin persiapan elo sekarang juga!
Rumus Keliling dan Rumus Luas Segitiga Siku Siku
Setelah paham konsep dari segitiga siku siku, sekarang kita coba pelajari rumus segitiga siku-siku, mulai dari luas hingga kelilingnya.
Rumus keliling segitiga siku siku:
K = sisi a + sisi b + sisi c
Rumus luas segitiga siku siku:
L = ½ x alas x tinggi
Tapi, gimana kalau ternyata salah satu sisi segitiga siku siku tersebut belum diketahui? Kamu harus menggunakan rumus apa untuk mendapatkan panjang sisi yang belum diketahui tersebut? Yap, caranya dengan menggunakan rumus phytagoras. Ini dia rumusnya:
c2 = a2 + b2 atau c = √a2 + b2
a2 = c2 – b2 atau a = √c2 – b2
b2 = c2 – a2 atau b = √c2 – a2
Contoh Soal dan Pembahasan
Rumus segitiga siku-siku mudah dimengerti, kan? Nah, supaya rumus keliling dan rumus luas segitiga siku siku bisa lebih mudah kamu pahami, perhatikan juga contoh soal dan pembahasan berikut ini ya!
Contoh Soal 1
Suatu segitiga siku siku memiliki sisi a, b, c berturut-turut 3, 4, dan 5. Tentukan keliling dari segitiga tersebut!
Pembahasan:
Diketahui: a = 3; b = 4; dan c = 5.
Ditanya: K
Jawab:
K = sisi a + sisi b + sisi c = 3 + 4 + 5 = 12 cm
Jadi, keliling segitiga abc adalah 12 cm.
Contoh Soal 2
Suatu segitiga siku siku memiliki sisi miring 13 cm. Tinggi segitiga tersebut adalah 5 cm. Hitunglah luas segitiga siku suku tersebut!
Pembahasan:
Diketahui: c (sisi miring) = 13 cm; b (tinggi) = 5 cm.
Ditanya: L
Jawab:
Pertama, kita harus mencari tau dulu berapa panjang alas segitiga tersebut. Caranya dengan menggunakan rumus phytagoras.
a2 = c2 – b2 = 132 – 52 = 169 – 25 = 144
a = √144 = 12 cm.
Setelah diketahui alasnya adalah 12 cm. Selanjutnya kita hitung luasnya.
L = ½ x alas x tinggi = ½ x 12 x 5 = 30 cm.
Jadi, luas segitiga siku siku tersebut adalah 30 cm.
Itu dia penjelasan mengenai rumus luas segitiga siku siku. Setelah kamu tahu pengertian dan rumusnya, ternyata sangat mudah ya dalam perhitungannya. Semoga penjelasan di atas dapat dengan mudah kamu pahami ya. Jadi, kalau nanti bertemu dengan soal yang menggunakan rumus segitiga siku-siku kalian tidak akan mengalami kesulitan.
Khusus buat Sobat Zenius yang ingin meningkatkan nilai rapor, sekaligus menambah pemahaman semua pelajaran sekolah. Kamu bisa gabung ke Zenius Aktiva lho. Di paket ini, kamu bakal diberikan akses ke ribuan video belajar premium, dibimbing langsung sama tutor di Live Class, Try Out buat persiapan ujian sekaligus latihan soal yang intensif lho. Yuk, cari tahu informasi lengkapnya dengan klik banner di bawah ini, sekarang!
Baca Juga Artikel Lainnya
Lihat Juga Proses Belajar Ala Zenius di Video Ini
Originally published: April 13, 2021
Updated by: Maulana Adieb & Rizaldi Abror
Ada sebuah segitiga 5h dengan panjang 6h5cm dn 5 13cm maka panjangberapa pnjang alas pada segitiga