Hai Sobat Zenius! Ketemu lagi, nih, sama gue. Di artikel kali ini gue akan bahas materi Grafik Fungsi Trigonometri. Materi yang katanya, sih, suka bikin pusing tujuh keliling.

Tapi, tenang-tenang. Kunci dari belajar Trigonometri adalah pahami langkah demi langkah untuk memahami materi dan mengerjakan contoh soalnya.

Nggak percaya? Yuk, buktiin bareng-bareng! Simak materi terkait Persamaan Grafik Fungsi Trigonometri hingga cara menggambarnya, yuk.

Daftar Isi

Apa itu Persamaan Grafik Fungsi Trigonometri?

Pernah nggak sih, elo kepikiran? Buat apa, sih, belajar Trigonometri? Mana susah banget, lagi!

Jangan salah! Ternyata Trigonometri banyak diterapkan di kehidupan sehari-hari, lho. Contohnya, untuk mengukur tinggi gedung-gedung pencakar langit hingga memperkirakan jarak benda-benda di luar angkasa.

Sesuai namanya, Persamaan Grafik Fungsi Trigonometri merupakan persamaan yang memuat Fungsi Trigonometri dari sudut yang belum diketahui nilainya. Gimana tuh, maksudnya? Cuzz, pelajari di bawah, ya!

Cara Menggambar Grafik Fungsi Trigonometri

Sebelum mulai menggambar Grafik Fungsi Trigonometri, elo harus tahu dulu, nih, jenis-jenis Fungsi Trigonometri. Mengapa? Karena beda fungsi beda pula grafiknya, dong.

Pembagian Jenis-jenis Fungsi Trigonometri tentu masih berkaitan dengan tiga sekawan trigonometri, yaitu sin, cos, dan tan.

Grafik Fungsi Sinus (y= sin x)

Nah, sekarang gue punya fungsi y=x. Gimana cara menggambar Grafik Fungsi Trigomometrinya? Masih inget, nggak?

Pertama, tentu nilai x-nya harus diketahui dulu, dong. Misal x = 1 karena y = x, maka nilai y juga 1.

Begitu pula ketika nilai x = 2, ya y-nya juga 2, dan seterusnya… Kalo elo masih bingung kira-kira gini gambarannya y=x.

x	y = x
1	1
2	2
3	3
4	4

Tabel y = x

Nah, baru deh elo gabungkan titik-titik tersebut hingga membentuk sebuah grafik seperti berikut.

Grafik yang Terbentuk dari Fungsi Sinus (y= sin x) — Grafik Fungsi Sinus (y= sin x)

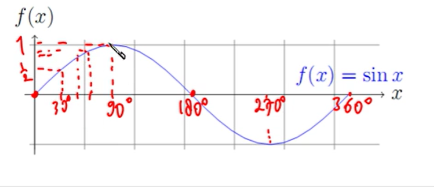
Nah, sekarang kalo gue punya nilai fungsi y= sin x. Gimana cara menentukan Grafik Fungsi Trigonometrinya?

Nah, untuk menentukan grafiknya, elo harus inget-inget lagi sudut istimewa. Nilai dari sudut istimewa berkaitan juga dengan materi Grafik Fungsi Trigonometri, lho. Untuk membantu elo mengingat nilai sudut istimewa sinus, perhatikan tabel berikut.

Tabel Sudut Istimewa Sinus (Sumber: Arsip Zenius)

Setelah nilai fungsi sinus diketahui, langkah selanjutnya adalah mengubah sin x menjadi angka-angka di atas. Dan masukkan ke grafiknya. Taraaa, jadi, deh, grafik kayak di bawah ini.

Gambar Grafik Fungsi y= sin x — Grafik Fungsi y= sin x (Sumber: Arsip Zenius)

Nah, kalau Persamaan Grafik Fungsi Trigonometrinya diubah menjadi y= a sin x dengan a = 3, grafiknya berubah lagi jadi seperti ini.

Gambar Grafik y=a sin x — Grafik y=a sin x (Sumber: Arsip Zenius)

Perubahan nilai a mengakibatkan perubahan amplitudo gelombang pada grafik di atas.

Oh iya, mungkin elo bertanya-tanya, kok grafik di atas nggak dicantumin angkanya? Emang boleh, ya? Yap, boleh-boleh aja, Sobat Zenius. Ini disebut juga grafik halus. Seperti yang gue gambarkan di atas.

Grafik Fungsi Cosinus (y = cos x )

Tadi kan elo udah nyoba bikin Grafik Fungsi Sin dari persamaan y= sin x. Sekarang, kalau persamaannya sedikit gue ubah jadi , gimana cara menggambar grafiknya, ya?

Kalo elo udah paham polanya harusnya udah kebayang cara ngerjainnya, sih. Masih inget, dong, apa langkah pertama yang harus elo lakuin?

Yoi, ketahui dulu nilai fungsi cosinusnya. Cek tabel di bawah ini, ya, untuk mengetahuinya.

Tabel Sudut Istimewa Cosinus (Sumber: Arsip Zenius)

Nah, kalau elo udah punya titik-titiknya, tinggal elo gambarkan ke diagram kartesius, deh. Sambil latihan, coba elo gambaran dulu, deh, grafiknya. Baru nanti kita cocokkan apakah sama atau nggak. Oke?

Mengerjakan Grafik Fungsi Cartesius — Mencoba Menggambar Grafik Fungsi Cartesius (Sumber: tenor.com)

Gimana? Udah selesai, kah? Coba kita cocokkan jawabannya, yuk!

Gambar di atas merupakan gambar Grafik Fungsi Cosinus yang terbentuk dari fungsi y= cos x . Gimana? Sama nggak dengan yang elo gambar?

Sebenarnya grafik di atas masih bisa dilanjutin lagi, lho. Gimana tuh, maksudnya?

Cosinus merupakan fungsi periodik yang selalu berulang setiap periodenya. Satu periode cosinus merupakan 360 derajat, artinya grafiknya akan berulang terus setiap 360 derajat.

Kalau gambarnya kita lanjutin terus, akan membentuk periode yang berulang seperti pada gambar di bawah ini.

Jadi, nggak ada kata mentok di fungsi cosinus, guys, baik yang di sebelah kanan maupun kiri. Dari gambar di atas pun sebenarnya masih terus dilanjutkan.

Grafik Fungsi Tangen (y = tan x)

Masih sama dengan cara menggambar kedua grafik sebelumnya. Elo harus tahu dulu sudut istimewa dan nilai fungsi tangen-nya. Kalau elo lupa, bisa cek pada gambar di bawah ini.

Tabel Sudut Istimewa dan Nilai Fungsi Tangen (y= tan x) — Tabel Sudut Istimewa dan Nilai Fungsi Tangen (Sumber: Arsip Zenius)

Untuk menggambar grafiknya, nggak jauh berbeda dengan cara menggambar grafik fungsi sinus dan cosinus.

Dari tabel di atas, elo kan udah punya titik-titik yang dibutuhkan untuk menggambar grafik, langsung aja masukkan titik-titik tersebut ke dalam diagram kartesius.

Grafik Fungsi Tangen (Sumber: Arsip Zenius)

Jadi deh, grafik y= tan x. Tapi, bentar-bentar. Ada yang bingung, nggak? Kok pada saat x=90 dan x=270nggak ada grafiknya? Kira-kira kenapa, ya?

Nah, coba elo balik lagi ke nilai fungsi tangen, deh. Nilai pada saat x=90 dan x=270 adalah nggak terdefinisi. Hal ini mengakibatkan grafiknya terpotong dan nggak tahu, nih, mau dibawa kemana hubungan kita~ eh kok jadi nyanyi?

Sama dengan cosinus, tangen juga merupakan fungsi periodik yang grafiknya selalu berulang setiap periodenya, lho. Bedanya, periode tangen bukan 360 derajat. Akan tetapi, 180 derajat. Maka, grafik tangen jika terus berulang akan menjadi seperti ini.

Cara Menggambar Grafik Fungsi Tangen — Grafik Fungsi Tangen (Sumber: Arsip Zenius)

Jadi, untuk menggambar Grafik Fungsi, baik sinus, cosinus, maupun tangen, elo harus inget langkah-langkah berikut:

Ketahui terlebih dahulu nilai fungsi sin, cos, maupun tan.
Dari nilai fungsi tersebut, elo bisa ketahui titik-titik yang akan digambarkan ke diagram kartesius.
Terakhir, gambar grafik fungsinya.

Contoh Soal Grafik Fungsi Trigonometri

Selesai juga pembahasan materi Grafik Fungsi Trigonometri. Gimana, Sobat Zenius? Semoga artikel ini bermanfaat dan bikin pemahaman materi Grafik Fungsi Trigonometri elo makin kece, ya!

Nah, untuk menguji pemahaman elo, gue udah siapin beberapa contoh soal Grafik Fungsi Trigonometri, nih! Langsung sikat, yuk!!

Perhatikan gambar di bawah ini.

contoh soal grafik fungsi trigonometri 1

pembahasan soal grafik fungsi trigonometri 1

Contoh Soal 2

Contoh Soal 3

Perhatikan gambar berikut.

pembahasan soal grafik fungsi trigonometri nomor 3

***

Oke, sebelum masuk ke penutup. Gue ingin ngingetin nih kalau Zenius punya paket belajar yang siap nemenin perjuangan elo! Klik gambar di bawah ini biar elo bisa rasain langsung serunya belajar bareng Zenius!

Sampai juga kita di penghujung artikel kali ini? Gimana? Trigonometri itu mudah bukan?

Materi yang susah itu bukan cuma untuk diucapkan aja, Sobat Zenius. Susah nggak akan jadi mudah kalau elo nggak berusaha mempelajarinya.

Gue jadi inget salah satu quotes Jerome Polin di bukunya yang berjudul Mantappu Jiwa (2019),

“Di mana ada niat, asal mau berusaha, pasti ada jalan”

So, tetap semangat belajar, ya! Nah, supaya pemahaman elo makin oke, elo bisa pelajari materi menggambar grafik fungsi trigonometri secara lengkap di Zenius, lho. Yuk, klik banner di bawah ini!