Wokey, Sobat Zenius. Kali ini, kita ketemu lagi nih sama aljabar, buat mempelajari turunan fungsinya.

Jadi gini, Sobat Zenius. Selama ini, kita udah pernah belajar fungsi secara umum, yang dinotasikan dengan simbol f(x).
Kali ini, kita bakal ngebahas turunan fungsi aljabar yang biasa dinotasikan dengan simbol f’(x). Wah, apa bedanya tuh f(x) dan f’(x)?
Coba bayangin deh. Misalnya, elo lagi naik mobil. Pas lagi sat set sat set ke sana ke sini, pasti ada yang namanya percepatan kan. Entah melambat, atau makin cepat.
Nah, kalo seandainya percepatan tersebut digambarkan dengan sebuah grafik, pasti ada garis fungsi yang menunjukkan perubahan kecepatan. Di situ tuh ada turunan fungsi, yang dinotasikan sebagai f’(x).
Kira-kira elo udah dapet gambarannya belum? Atau, elo justru tambah bingung? Wkwkwk, tenang dulu, Sobat Zenius.
Di artikel ini, kita coba bedah aja yuk apa itu turunan fungsi aljabar, dimulai dari pengertiannya, serta melihat beberapa rekomendasi video materinya.
Daftar Isi
Pengertian Turunan Fungsi Aljabar
Pertama-tama, kita bahas konsep turunan dulu ya. Dengan memahaminya, kita bisa tahu nih sifat-sifat turunan fungsi aljabar. Coba elo lihat grafik di bawah ini.
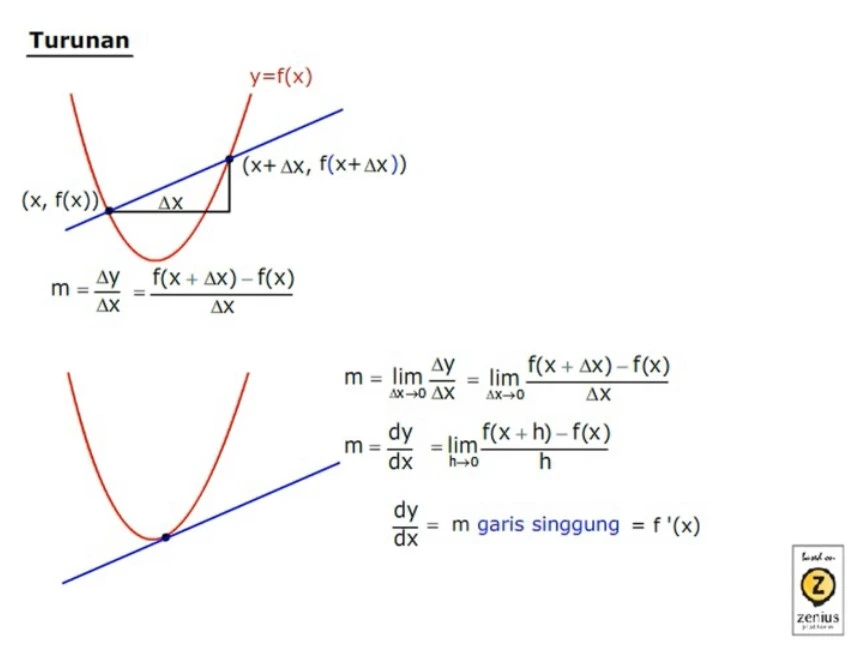
Di grafik di atas, elo bisa melihat ada grafik fungsi y=f(x), yang ditandakan dengan sebuah kurva warna merah.
Selanjutnya, kita coba masukkan dua titik yang membentuk garis biru. Nah, garis tersebut berarti memiliki dua titik, yaitu titik (x, f(x)) dan ((x+Δx), f(c+Δx).
Dari mana Δx itu? Kita bisa lihat, itu dari perubahan jarak dari titik pertama ke titik kedua. Iya, seperti biasa delta (Δ) itu digunakan untuk menggambarkan perubahan nilai ya, Sobat Zenius.
Kembali lagi ke materi, tentunya garis seperti itu memiliki kemiringan alias gradien(m). Elo masih ingat nggak gimana cara nyari gradien?
Ini nih model matematika untuk mencari gradien.
Elo tinggal membagi Δy dengan Δx. Lebih jelasnya, elo bisa baca pada artikel di bawah ini.
Baca Juga: Rumus Gradien (Kemiringan) Garis Lurus dalam Matematika
Nah, kira-kira gimana nih cara dapetin gradien dari grafik di atas? Ya kita tinggal masukkan titik y dan x ke formula tersebut. Bisa kita tuliskan seperti ini.
Selanjutnya, kita andaikan, misalnya dua titik tadi tuh bergeser ke bawah, sampe deket banget, tapi nggak nempel. Berarti ada limit ya, bahwa beda nilainya tuh deket banget sama nol, tapi nggak nol alias nggak nempel.
Nah, dalam keadaan seperti itu, garis lurus tadi menjadi garis singgung seperti di bawah ini.
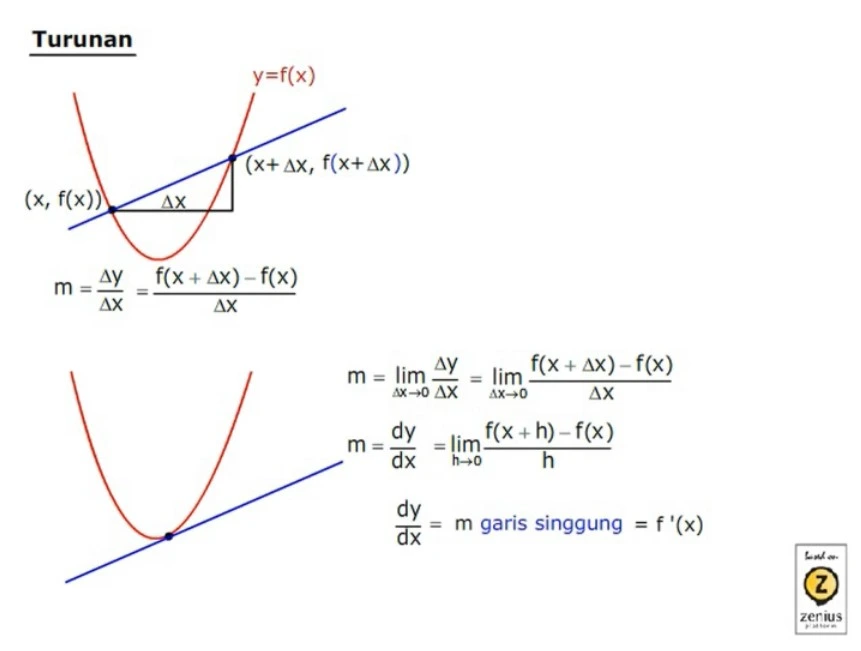
Untuk mencari gradien garis singgung di atas, rumusnya masih sama kan, Sobat Zenius? Cuma, sekarang ada limitnya.
Baca Juga: Memahami Limit Fungsi Aljabar – Materi Matematika Kelas 11
Nah, ini dia nih, gradien garis singgung itu sama dengan definisi turunan yang kita tulis sebagai dy per dx.
Jadi m garis singgung alias dydx adalah turunan f(x), yang dinotasikan sebagai f’(x).
Oleh karena itu, kalo kita simpulkan, gradien garis singgung tadi itu adalah turunan fungsi ya, Sobat Zenius.
Untuk pembahasan yang lebih mantap tentang konsep turunan tadi, gue saranin elo nonton video materi Zenius di bawah ini, deh.
Video Materi: Definisi Turunan
Terus gimana nih cara menghitung turunan fungsi aljabar? Untuk menjawab itu, mari kita bahas rumusnya.
Rumus Turunan Fungsi Aljabar
Sesuai dengan pembahasan tentang pengertian turunan tadi, rumusnya itu masih sama ya dengan cara mencari gradien untuk dua titik pada umumnya.
Tapi ingat, ada limitnya. Selain itu, untuk mempermudah pembedaan, Δx pada fungsi turunan biasanya diubah menjadi h. Inilah rumusnya.

Tanda panah kuning di atas menunjukkan bahwa notasi turunan fungsi aljabar itu bisa bermacam-macam ya.
Bisa digambarkan sebagai m dari sebuah garis singgung, bisa juga sebagai dydx, atau sebagai f’(x).
Cakep, kita udah tahu rumusnya nih. Sekarang, gimana ya aplikasi turunan fungsi aljabar? Biar kita paham akan penerapan turunan fungsi aljabar, kita langsung lihat contoh-contoh soalnya aja, yuk!
Contoh Soal Turunan Fungsi Aljabar
Untuk contoh turunan fungsi aljabar, kita bahas berbagai macam soal dari yang simpel dulu deh.
Contoh Soal 1: f(x) = 1.000.000
Gimana turunan fungsinya?
Katanya dimulai dari yang gampang, kok langsung dimulai dari 1.000.000? Sebelum elo demo di depan rumah gue, soal ini beneran gampang banget, Sob.
Nih, biar paham dan nggak cuma hafal rumus, kita bikin grafiknya ya.
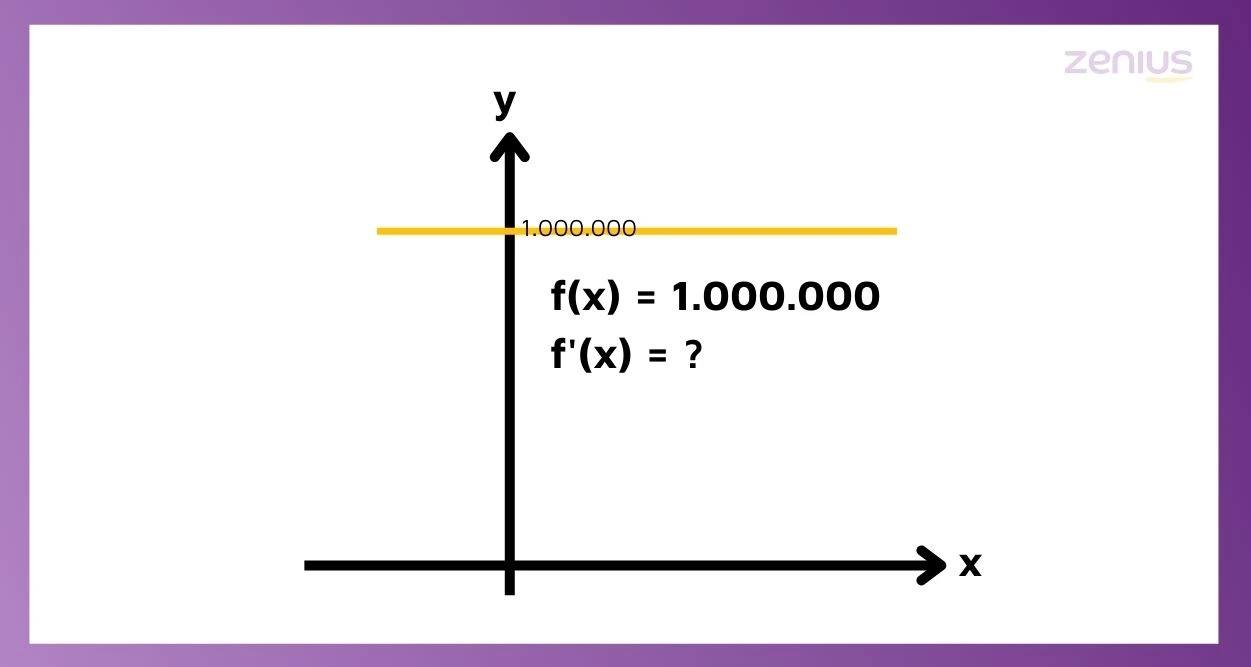
Sobat Zenius, kalo elo beneran paham sama konsep turunan yang udah dibahas tadi, elo sebenarnya bisa tahu jawabannya tanpa pakai rumus apapun lho.
Ingat, turunan fungsi itu kan gradien (kemiringan) garis singgung. Jadi, kalo garisnya lurus kayak gitu, otomatis kemiringannya nol dong.
Sebenarnya, cara gampang lain, kalo di fungsi awal nggak ada x, pasti turunannya nol. Namun, ngerti cara gampang hafalan seperti itu nggak cukup ya. Sebaiknya, kita benar-benar paham konsep serta grafik dari fungsi tersebut.
Nah, biar lebih yakin lagi, gue coba pakai rumus yang tadi deh, buat ngecek apakah benar hasilnya nol.
Wah, beneran ya, hasilnya 0. Dari sini bisa kita simpulkan, berapapun nilainya, mau seratus, sejuta, satu miliar, atau bahkan satu triliun pun, fungsi turunannya akan menjadi nol, bila nggak ada x.
Terus, gimana kalo seandainya ada x? Kita pindah ke soal selanjutnya, yuk.
Contoh Soal 2: f(x)= 2x
Oke, di soal kali ini, ada x nih. Elo familiar nggak sih sama model fungsi seperti itu? Elo harusnya udah pernah ketemu ini ketika belajar fungsi linear.
Simpelnya, kita tinggal input nilai x, untuk mendapatkan nilai f(x) alias y. Kira-kira, grafiknya kayak gimana, nih? Coba gambar dulu ah.
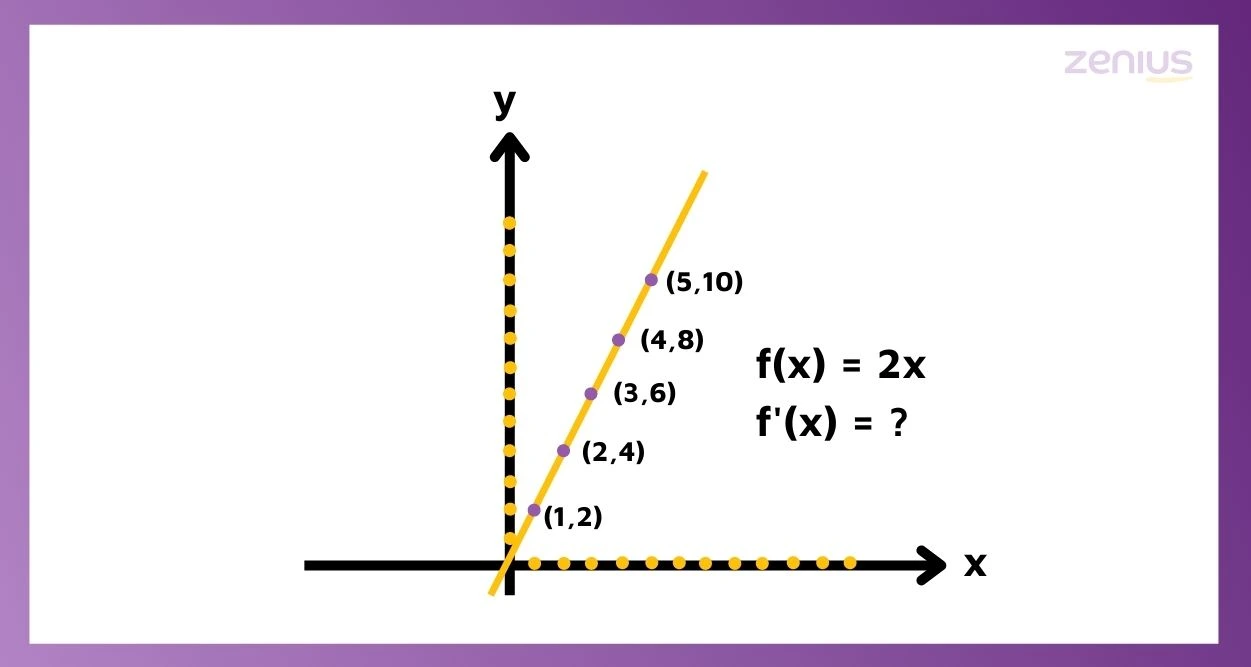
Nah, Sobat Zenius bisa lihat, fungsi tadi membentuk garis lurus dengan gradien nih. Elo masih ingat nggak gimana cara cari gradien garis lurus? Formulanya adalah y=mx+c.
Dari rumus di atas, terlihat bahwa gradien (m) itu menempel dengan x. Berarti berapa nih gradien dari f(x)=2x? Bener banget, gradiennya 2.
Selanjutnya, seperti yang udah kita bahas di bagian pengertian, gradien pada fungsi turunan itu nilainya sama dengan fungsi pertama. Berarti, gradien fungsi turunannya ya 2 juga.
Nih, kita coba tes dengan rumus yang udah kita pelajari ya.
Cara gampangnya, kalo ada angka yang nempel dengan x, pasti angka tersebut adalah gradiennya, Sobat Zenius.
Terus, kalo seandainya ada koefisien, misalnya f(x)=2x+3, gimana nih, Sob? Singkat cerita, tetap 2 jawabannya.
Gampangnya, angka 3 di situ nggak ada x, maka dia jadi nol. Lalu angka yang nempel sama x itu adalah gradien (m), jadi tinggal 2 deh.
Baca Juga: Definisi Fungsi Linear dan Contohnya – Matematika Kelas 10
*********
Oke Sobat Zenius, itulah pembahasan singkat mengenai turunan fungsi aljabar . Kalo elo ingin mempelajari materi ini dan materi Matematika lainnya dengan lebih dalam dan asyik, coba deh nonton video persiapan UTBK Zenius dan akses soal-soalnya.
Pastikan elo log in akun Zenius elo ya supaya bisa akses video dan soalnya. Sampai di sini dulu artikel kali ini, dan sampai jumpa di artikel selanjutnya!










Leave a Comment