Halo Sobat Zenius? Apa kabar nih? Masih semangat belajarnya kan? Kali ini, aku mau ngajak kamu membahas rumus gradien garis lurus, cara mencari hingga contoh soal dan penyelesaiannya. Yuk, baca artikel ini sampai selesai!

Sebagai permulaan, aku punya analogi sederhana nih. Pernah nggak sih kamu mengamati kenapa tangga dibangun dengan sangat presisi? Nah, dalam membuat tangga, ada ilmu matematika yang diaplikasikan lho. Yap, betul sekali dalam membuat tangga yang presisi, diperlukan rumus gradien.

Coba bayangkan kalau saat pembangunan tangga asal-asalan tanpa memperhatikan kemiringannya, bisa-bisa nanti setelah jadi dan siap digunakan malah jarak antar tangga terlalu jauh.

Hal itu bisa mencelakai banyak orang, termasuk kamu yang melintasinya. Maka dari itu, kamu perlu mengetahui apa itu gradien dan bagaimana sih rumus gradien itu? Bagaimana cara mencari gradien? Yuk, simak penjelasan di bawah ini!

Daftar Isi

Apa Itu Gradien?

Di atas kita udah menyinggung sedikit tentang gradien. Lantas, apa sih gradien itu? Gradien adalah nilai yang menunjukkan kemiringan suatu garis lurus. Sebelum membahas tentang gradien, alangkah baiknya kamu mengetahui materi persamaan garis terlebih dahulu.

Persamaan garis bisa dituliskan dengan y = mx + c. Nah, gradien dinotasikan dengan huruf “m” dari persamaan garis tersebut. Nantinya, gradien akan menentukan seberapa miring sih suatu garis pada titik koordinatnya.

Bisa miring ke kanan atau ke kiri, dan bisa juga landai atau curam. Untuk garis yang miring ke kanan, maka gradiennya bernilai positif, sedangkan yang miring ke kiri akan bernilai negatif.

Oh iya, buat kamu yang belum punya aplikasi Zenius, yuk, download apps-nya dengan klik banner di bawah ini! Pilih yang sesuai dengan device yang kamu gunakan ya!

Download Aplikasi Zenius

Tingkatin hasil belajar lewat kumpulan video materi dan ribuan contoh soal di Zenius. Maksimaln persiapanmu sekarang juga!

Sifat Gradien dari Dua Garis Lurus

Suatu garis bisa memiliki kedudukan sejajar atau tegak lurus. Nah, hubungan keduanya bisa membuat nilai gradiennya saling berhubungan. Dengan kamu mengetahui sifat dari kedua garis lurus, maka kamu akan lebih mudah dalam menebak atau menentukan gradien dari kedua garis tersebut.

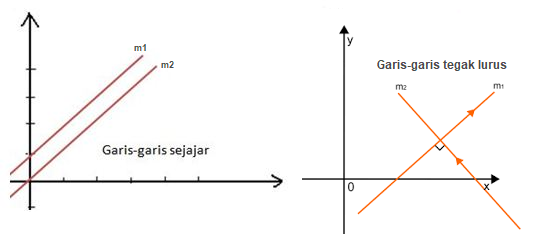
Dua Garis Sejajar

Dua garis sejajar berarti antara garis A dan B saling sejajar. Dengan begitu, gradien kedua garis tersebut adalah sama.

mA = mB

Dua Garis Tegak Lurus

Ketika ada dua garis yang saling tegak lurus, maka hasil kali kedua gradiennya adalah -1.

mA x mB = -1

Rumus Gradien dan Contoh Soalnya

Setelah paham pengertian dari gradien, selanjutnya kita masuk ke rumus gradien. Secara umum, cara mencari gradien bisa dilakukan dengan tiga cara nih, guys. Penasaran ada cara apa aja? Ini dia ketiga cara untuk mencari gradien.

Mencari Gradien Persamaan Linier

Persamaan linier ada dua bentuk, yaitu y = mx + c dan ax + by + c = 0. Karena keduanya berbeda, maka cara menentukannya juga berbeda, guys.

Persamaan garis y = mx + c

Dari persamaan garis seperti ini, gradien akan mudah dicari, yaitu “m”. Supaya lebih jelas, kamu bisa lihat contoh di bawah ini:

Garis y = 2x + 3, maka gradien garis tersebut adalah 2.
Garis y = -2x + 5, maka gradien garis tersebut adalah -2.

Iya, hanya seperti itu, mudah ‘kan?

Persamaan garis ax + by + c = 0

Nah, sekarang kita coba cari gradien dari persamaan ax + by + c = 0. Sebenarnya konsepnya sama, di mana kamu harus mengubah persamaan ini ke dalam y = mx +c, dengan begitu kamu bisa menemukan m sebagai gradiennya. Gimana caranya? Coba perhatikan contoh soal di bawah ini ya!

Hitunglah gradien dari persamaan garis 3x + 2y – 5 = 0!

Jawab:

Pertama, kamu ubah dulu persamaan 3x + 2y – 5 = 0 menjadi bentuk y = mx + c. Jadilah seperti ini:

2y = -3x + 5.

Perhatikan nilai positif dan negatifnya ya, guys. Kok 3x jadi bernilai negatif? Itu karena 3x dan -5 pindah ruas. Yang awalnya berada di ruas kiri, pindah menjadi ruas kanan. Ingat ya, kalau pindah ruas, berarti +/- juga ikut berubah.

Kedua, karena nilainya masih 2y, maka kita bagi persamaan di atas dengan angka 2, supaya persamaannya menjadi y = mx + c. Maka, menjadi seperti ini:

y = -3/2x + 5/2

Sekarang, kamu udah bisa menentukan yang mana nilai gradiennya. Yap, gradien dari persamaan di atas adalah -3/2.

Mencari Gradien dengan Dua Titik

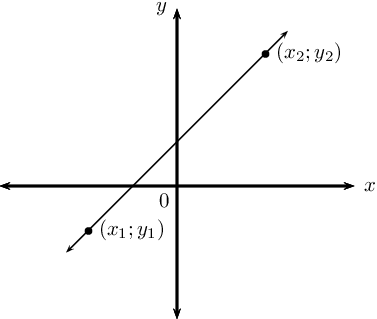
Selanjutnya, kalau kamu menemukan persamaan dari dua titik, maka gunakan rumus m = y2 – y1 / x2 – x1. Dua titik itu maksudnya gimana sih, kak? Kamu coba amati gambar berikut ini:

Misalnya, garis pada gambar di atas terdapat pada dua titik (-3,2) dan (5,3). Bagaimana cara menghitung gradiennya? Yuk, simak pembahasan di bawah ini!

Anggaplah titik (x1,y1) = (-3,-2) dan (x2,y2) = (5,3). Sekarang coba masukkan angka tersebut ke dalam rumus gradien dua titik:

m = Δy/Δx = y2 – y1 / x2 – x1

m = 3 – (-2) / 5 – (-3) = ⅝

Jadi, gradien garis tersebut adalah ⅝. Kamu bebas kok memilih mana yang akan dijadikan titik (x1,y1) dan (x2,y2). Hasilnya akan sama aja ya, guys.

Nah, itu dia penjelasan tentang cara mencari rumus gradien & contoh soalnya guys. Gimana sudah makin paham kan?

Biar makin mantap, Zenius punya beberapa paket belajar yang bisa lo pilih sesuai kebutuhan lo. Di sini lo nggak cuman mereview materi aja, tetapi juga ada latihan soal untuk mengukur pemahaman lo. Yuk langsung aja klik banner di bawah ini!