Vektor dua dimensi dan vektor tiga dimensi bedanya apa sih? Eh bentar bentar, vektor itu apaan sih? Wah, elo perlu paham mengenai vektor nih, karena materi ini sering muncul dalam UTBK.
“John, gue mau main ke rumah elo dong. Kasih tau gue arah-arahnya dari sekolahan ya, sekarang, cepet!”
“Oke oke, dari sekolahan elo bisa langsung ambil jalan pintas ke gang kecil yang ada di Barat Laut. Terus elo ikutin jalan aja sampai ketemu rumah warna merah.”
Kalau digambarkan, perjalanan Soni ke rumah John bisa seperti ini.
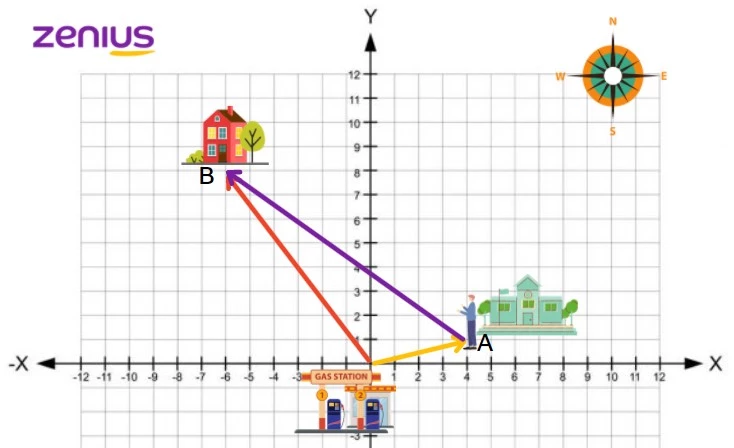
Nah, perjalanan Soni ke rumah John bisa dihitung menggunakan vektor. Hmm … apa itu vektor? Di kelas 10, elo sudah belajar mengenai vektor. Sekarang, kita bahas vektor yang sering muncul dalam soal UTBK ya.
Daftar Isi
Apa Itu Vektor?
Di Matematika dan Fisika, ada dua jenis besaran, yaitu besaran skalar dan vektor. Besaran skalar merupakan suatu benda yang hanya memiliki nilai besaran. Contohnya waktu dan massa. Sedangkan, besaran vektor merupakan suatu benda yang memiliki nilai besaran dan arah. Contohnya perpindahan, kecepatan, dan percepatan.
Biasanya, vektor dilambangkan dengan anak panah, dimana pangkal anak panahnya menunjukkan titik awal vektor dan ujung anak panahnya menunjukkan titik ujung vektor. Misalnya gini, elo lagi berdiri di rumah A, kemudian berjalan hingga tiba di rumah B. Sehingga, perjalanan elo bisa dilambangkan dalam vektor seperti ini.
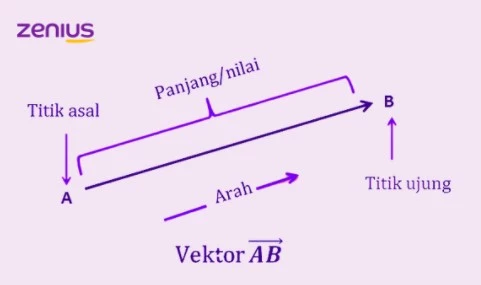
Gimana, sudah mulai tergambar ya seperti apa notasi dan arah vektor? Namun, vektor itu nggak hanya dinotasikan dengan . Vektor juga bisa dinotasikan dengan huruf
.
Baca Juga: Materi Lengkap Besaran dan Satuan Fisika
Vektor Dua Dimensi
Vektor dua dimensi juga seringkali disebut dengan vektor bidang. Nah, pada vektor ini, kita akan mengenal yang namanya vektor posisi. Apa itu vektor posisi?
Vektor posisi adalah vektor yang pangkalnya ada di pusat koordinat (0,0) dan ujungnya di suatu titik (x,y).
Supaya lebih tergambar mengenai vektor posisi, elo bisa perhatikan koordinat kartesius berikut ini.
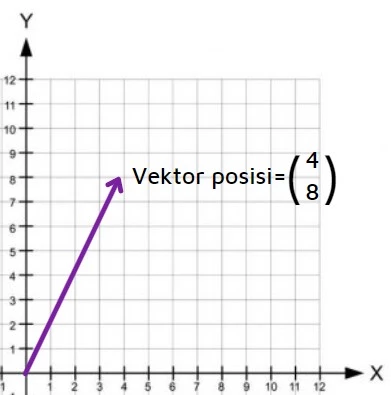
Kemudian, muncul pertanyaan seperti ini, “Bisa nggak kalau ada garis yang terbentang dari titik (x,y) ke titik (a,b)? Bisakah menghitung vektornya? Gimana caranya?”. Jawabannya adalah bisa. Contohnya seperti ini.
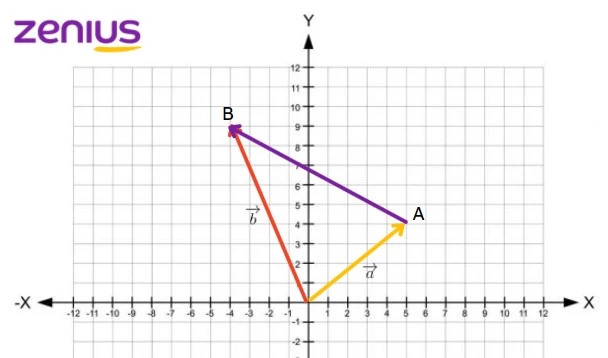
Dari koordinat kartesius di atas, kita bisa mendapatkan informasi bahwa:
(dari titik A jalan ke kiri sejauh 9 satuan, kemudian naik ke atas sejauh 5 satuan)
Nah, kalau kita tarik garis dari titik (0,0) ke titik A menjadi dan
, maka:
Nah, betul kan? Jadi, bisa ditarik kesimpulan bahwa vektor posisi OB dikurangi vektor OA akan menghasilkan vektor AB. Sekarang kita coba masuk ke contoh soal yang biasa muncul dalam UTBK. Kurang lebih gambaran soalnya akan seperti ini.
Perhatikan ilustrasi vektor di bawah ini!
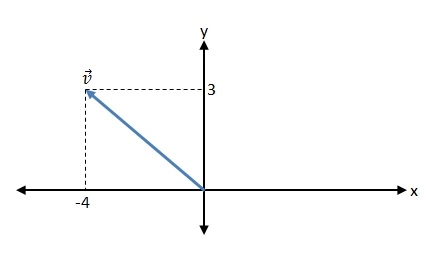
Tentukan penulisan notasi dan besaran vektor pada dimensi dua di atas!
Oke, kita coba jawab bareng-bareng ya.
Apa nih yang diketahui? Komponen vektor pada sumbu x
= -4.
Komponen vektor pada sumbu y
= 3.
Selanjutnya, kita cari notasi vektor , yaitu:
Terakhir, kita cari besaran vektor , yaitu:
Jadi, penulisan notasi dan besaran vektor pada dimensi dua di atas adalah dan
.
Gimana, mudah kan? Setelah mengetahui pengertian dan perhitungan pada vektor dua dimensi. Kira-kira elo kebayang nggak sih, apa aplikasi vektor dimensi dua dalam kehidupan sehari-hari?
Kalau menurut gue, vektor dua dimensi ini bisa diaplikasikan saat elo sedang bermain terjun payung. Ketika elo turun dari pesawat, maka elo nggak akan jatuh lurus persis di bawah pesawat, iya kan? Pasti elo akan terbawa arah angin hingga akhirnya elo mendarat dengan selamat. Nah, lintasan elo dari turun dari pesawat hingga mendarat itu sama seperti perhitungan vektor, karena ada besaran dan arah.
Baca Juga: Kumpulan Rumus Vektor Matematika dengan Contoh Soal
Vektor Tiga Dimensi
Selanjutnya, kita bahas juga nih mengenai vektor tiga dimensi atau vektor dalam ruang. Tipe soal mengenai materi ini sering muncul di UTBK lho, guys. Sebenarnya, vektor tiga dimensi nggak jauh beda kok dari vektor dua dimensi. Bedanya, titik pada koordinat kartesiusnya ada tiga, yaitu x, y, dan z.
Jadi, notasinya akan menjadi seperti ini.
Nah, kalau digambarkan dalam diagram kartesius, maka bentuknya seperti bangun ruang di bawah ini.
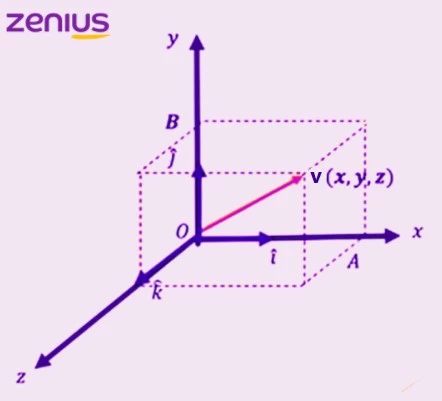
Gimana cara menentukan panjang vektor atau besaran pada vektor? Sama seperti pada vektor bidang, elo bisa menggunakan Teorema Pythagoras.
Jadi, kurang lebih perhitungannya sama seperti pada vektor bidang, hanya saja ada penambahan titik z pada vektor dalam ruang.
Oh iya, uraian di atas juga bisa elo pelajari menggunakan video belajar Zenius dengan klik banner di bawah ini, lho.
Baca Juga: Sejarah dan Cerita di Balik Teorema Pythagoras
Contoh Soal Vektor Dua Dimensi dan Tiga Dimensi
Untuk menguji sejauh mana pemahaman elo mengenai materi vektor dua dimensi, gue ada beberapa contoh soal dan pembahasan yang bisa dijadikan sebagai referensi. Cekidot!
Contoh Soal 1
Ada suatu vektor X yang memiliki besaran 10 satuan. Berdasarkan data tersebut, kira-kira berapakah vektor -X seharusnya?
A. Vektor -X harus memiliki besar -10 satuan dan arah sama dengan vektor X.
B. Vektor -X harus memiliki besar 10 satuan dan arah sama dengan vektor X.
C. Vektor -X harus memiliki besar 10 satuan dan arahnya berlawanan dengan vektor X.
D. Vektor -X harus memiliki besar 10 satuan dan arahnya tegak lurus dengan vektor X.
E. Vektor -X harus memiliki besar -10 satuan dan arahnya tegak lurus dengan vektor X.
Jawab: C. Vektor -X harus memiliki besar 10 satuan dan arahnya berlawanan dengan vektor X.
Pembahasan: Jika suatu besaran vektor ditulis -X, artinya arahnya berlawanan dengan vektor X. Tetapi, besarnya sama alias nggak berubah, yaitu sama dengan vektor X.
Contoh Soal 2
Perhatikan diagram kartesius berikut ini!
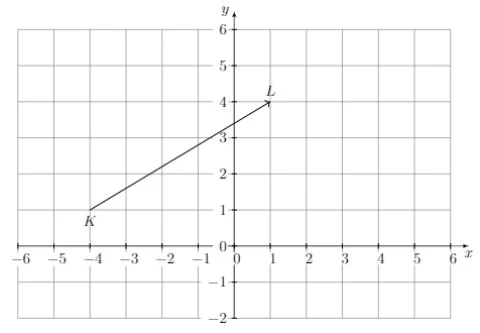
Tentukan vektor di atas!
Jawab: .
Pembahasan: Lihat perpindahan titik K ke L. Dari titik K pindah ke kanan sebanyak 5 satuan, kemudian ke atas sebanyak 3 satuan.
Contoh Soal 3
Sebutkan aplikasi vektor tiga dimensi dalam kehidupan sehari-hari!
Gimana, sudah ada gambaran kan mengenai vektor dalam ruang? Nah, kali ini gue mau tahu, seberapa paham sih elo dengan vektor tiga dimensi sampai bisa memberikan contoh aplikasinya dalam kehidupan sehari-hari. Elo juga bisa share jawaban di kolom komentar ya!
*****
Gimana nih, sampai sini udah paham kan tentang vektor dua dimensi dan tiga dimensi? Buat yang lebih menyukai belajar dengan nonton video, elo bisa mengakses materi UTBK lainnya di video Zenius. Elo juga bisa mencoba melatih kemampuan dengan level soal yang mirip UTBK beneran di Try Out bareng Zenius.
Baca Juga: Materi dan Contoh Soal Pengetahuan Kuantitatif – TPS UTBK









Leave a Comment