Pengertian Teorema Bayes dan Contoh Soalnya – Materi Matematika Kelas 12

Sekarang elo bisa berasumsi menggunakan teorema Bayes, sehingga hasil stalking gebetan atau kepo mendengarkan curhatan orang bisa lebih logis dan matematis lagi.

Halo, Sobat Zenius! Elo pasti pernah kan mendengarkan curhatan teman, kemudian elo penasaran tentang siapa sosok yang diceritakannya? Misalnya seperti yang dialami oleh Kinan dan Aris berikut ini:

Aris : “Nan, tadi gue abis ngobrol sama orang di cafe, seru banget orangnya, dia juga baik, lho.”

Informasi pertama yang diperoleh Kinan adalah si Aris abis ngobrol sama orang di cafe. Kemudian, Kinan berasumsi bahwa orang yang ngobrol sama Aris adalah wanita.

Aris : “Oh iya, tadi dia pakai baju pink.”

Nah, Kinan dapat informasi tambahan nih kalau orang yang ngobrol sama Aris tadi memakai baju berwarna pink. Wah, keyakinan Kinan mengenai orang tersebut adalah wanita semakin bertambah dong. Tapi, nggak menutup kemungkinan juga kalau Aris ngobrol sama seorang pria yang memakai baju berwarna pink.

Nah, besar kemungkinan dari hipotesis atau asumsi-asumsi Kinan itu bisa dihitung secara matematis lho, guys. Gimana caranya? Caranya dengan menggunakan teorema Bayes atau kaidah Bayes.

Baca Juga: Pengertian Hipotesis dan Informasi Penting Lainnya

Apa Itu Teorema Bayes?

Pengertian teorema Bayes, yaitu:

“Teorema Bayes yaitu suatu formula yang menjelaskan bagaimana caranya memperbarui sebuah probabilitas dari suatu hipotesis saat kita udah menemukan suatu bukti atau petunjuk baru.”

Nah, bisa dikatakan juga sebagai suatu teorema dengan dua penafsiran yang berbeda. Teori ini menyatakan seberapa jauh sih suatu derajat kepercayaan subjektif harus berubah secara rasional ketika ada bukti baru.

Formula dari teorema Bayes adalah sebagai berikut:

Sehingga,

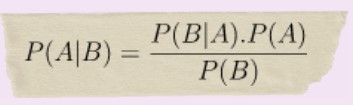
Baca Juga: Distribusi Peluang Kontinu – Materi Matematika Kelas 12

Aplikasi Teorema Bayes

Balik lagi ke cerita di awal tentang Aris yang ngobrol sama orang di cafe. Anggaplah kita adalah Kinan yang lagi bikin asumsi-asumsi tentang sosok yang ngobrol sama Aris. Berapa sih kemungkinan Aris ngobrol sama wanita? Gitu kan ya.

Nah, kita pakai teorema Bayes untuk menentukan berapa peluang Aris ngobrol sama wanita.

Kita tulis asumsi bahwa besar peluang Aris ngobrol sama wanita dari informasi pertama adalah 50%. Angka ini hanya asumsi bahwa populasi wanita di bumi adalah setengah dari populasi.

P(W) = 50% = 0,5

P(P) = 50% = 0,5

Setelah Aris bilang kalau orang yang ngobrol bareng sama dia memakai baju pink, maka kita punya informasi tambahan nih. Peluang orang berbaju pink adalah wanita itu kan besar ya, katakanlah 75%. Sedangkan, peluang pria memakai baju berwarna pink tentu lebih kecil, karena mayoritas pria nggak suka pakai warna pink, katakanlah jumlahnya 30%.

P(BP|W) = 75% = 0,75

P(BP|P) = 30% = 0,3

Nah, sekarang kita mencari tahu, berapakah kemungkinan wanita berbaju pink?

Dari aturan Bayes di atas, kita bisa substitusi kategorinya sesuai dengan yang akan kita cari.

Bingung nggak gimana cara mencari P(BP), karena di asumsi belum diketahui besaran peluangnya? Elo nggak usah bingung, masih ingat tentang materi probabilitas total nggak? Nah, elo bisa mencarinya menggunakan rumus probabilitas total.

P(BP) = P(BP|W).P(W) + P(BP|P).P(P) = (0,75)(0,5) + (0,3)(0,5) = 0,525

Kita masukkan ke dalam formula aturan Bayes, sehingga:

Jadi, dengan asumsi bahwa peluang Aris ngobrol sama wanita adalah 50% (berdasarkan setengah populasi). Tapi, dengan adanya informasi tambahan berupa baju pink, maka keyakinan Kinan bisa bertambah menjadi 71,4%.

Sampai sini paham ya menggunakan aplikasi teorema Bayes?

Baca Juga: Rumus Peluang dan Aplikasinya dalam Kehidupan Sehari-hari

Contoh Soal Teorema Bayes

Sampai sini udah paham kan sama materinya? Nah, untuk menguji sejauh mana pemahaman elo mengenai materi di atas, coba selesaikan contoh soal di bawah ini dan pahami pembahasannya, yuk!

Contoh Soal 1

Diketahui P(A)=0,4; P(B)=0,3; P(B|A)=0,65. Berapakah nilai dari P(A|B)?

a. 13/20

b. 7/12

c. 13/15

d. ⅕

e. 2/7

Jawab: c. 13/15

Pembahasan: 

Diketahui P(A)=0,4; P(B)=0,3; P(B|A)=0,65.

Sehingga, P(A|B) adalah sebagai berikut:

Contoh Soal 2

Pada penyakit yang diderita oleh 10% populasi penduduk terdapat sebuah alat uji dengan akurasi 95% mendeteksi penderita penyakit tersebut. Namun, alat tersebut memiliki kemungkinan 5% salah mendeteksi orang tidak sakit menjadi sakit. Jika seseorang dideteksi sakit oleh alat ini, sebenarnya berapa persen kemungkinan ia benar-benar sakit?

a. 77,855%

b. 67,857%

c. 50%

d. 45,382%

e. 33,333%

Jawab: b. 67,857%

Pembahasan:

Diketahui: P(sakit)=10%; P(tidak sakit)=90%; P(dideteksi sakit|sakit)=95%; P(dideteksi sakit|tidak sakit)=5%.

Kita cari dulu peluang dideteksi sakitnya.

P(dideteksi sakit) = P(dideteksi sakit|sakit).P(sakit) + P(dideteksi sakit|tidak sakit).P(tidak sakit) = 95%.10% + 5%.90% = 0,095 + 0,045 = 0,14.

Sehingga, yang akan dicari adalah P(sakit|dideteksi sakit).

Contoh Soal 3

Diketahui P(A)=0,35; P(B)=0,4; P(A|B)=0,55. Berapakah nilai dari P(B|A)?

a. 11/20

b. 7/13

c. 22/35

d. 17/32

e.½

Jawab: c. 22/35

Pembahasan: 

Diketahui P(A)=0,35; P(B)=0,4; P(A|B)=0,55.

*****

Gimana nih, sampai sini udah paham kan tentang teorema Bayes? Buat yang lebih menyukai belajar dengan nonton video, elo bisa mengakses materi ini di video belajar Zenius dengan klik banner di bawah ini menggunakan akun yang sudah didaftarkan di website dan aplikasi Zenius sebelumnya, ya!