Materi Pertidaksamaan Rasional dan Irasional Beserta Contoh Soal dan Pembahasan

Halo, Sobat Zenius! Balik lagi sama gue Grace. Kalau sebelumnya kita udah membahas persamaan dan pertidaksamaan nilai mutlak, kali ini gue mau mengajak elo semua buat membahas materi pertidaksamaan rasional dan irasional beserta contoh soal dan pembahasannya.

Wah, maksudnya rasional dan irasional gimana, ya? Lalu apakah ada gunanya kita belajar materi ini buat kehidupan kita? Yang jelas paham konsep materi ini bakal bantu elo buat mengerjakan soal-soal PTS nantinya.

Nggak cuman materinya aja, gue juga mau ngasih tahu contoh soal pertidaksamaan rasional dan irasional kepada elo semua. Tanpa berlama-lama lagi, yuk kita pahami dulu apa sih pertidaksamaan rasional dan irasional.

Apa Itu Pertidaksamaan Rasional dan Irasional?

Di dalam Matematika, ketika ada dua atau lebih hal yang bernilai sama maka akan diberi tanda sama dengan (=).

Sedangkan, bila ada dua atau lebih hal yang nilainya nggak sama akan diberi tanda lebih dari atau kurang dari seperti < , >,  ≤, ≥, dan ≠.

Nah, kali ini akan pakai notasi-notasi pertidaksamaan tadi bersama dengan bilangan rasional dan bilangan irasional.

Itu dia sekilas pengertian pertidaksamaan rasional dan irasional satu variabel. Sebelum berlanjut ke pembahasan bilangan rasional dan irasional, gue mau ngasih tahu ke elo semua buat download aplikasi Zenius dari sekarang!

Mengapa demikian? Lewat aplikasi, elo bisa mengakses ribuan video premium dari Zenius beserta contoh soal dan pembahasannya.

Nggak cuman itu, elo juga bisa menikmati fitur-fitur belajar lainnya, seperti ZenCore, ZenBot, dan simulasi ujian try out.

Jadi, tunggu apa lagi? Download aplikasinya sekarang, yuk!

Apa Itu Bilangan Rasional dan Irasional?

Terus bilangan rasional dan irasional itu apa? 

Bilangan rasional merupakan bilangan yang bisa dinyatakan sebagai pecahan a per b dengan catatan a dan b adalah bilangan bulat.

Ketika bilangan rasional berbentuk desimal, maka angkanya akan berhenti pada angka tertentu. Kalaupun nggak berhenti, ada pola pengulangan. Maksudnya gimana tuh? Biar nggak bingung coba lihat contoh di bawah ini yuk.

Misalnya ½ itu kalau jadi desimal 0,5 kan. Jadi berhenti sampai di angka 5 aja. Itu bilangan rasional.

Ada juga kasus di mana ketika pecahannya diubah jadi desimal tidak berhenti. Misalnya 7/11 = 0,6363636363… nah bisa dilihat ada polanya kan?

Lalu, gimana dengan bilangan irasional?

Bilangan irasional merupakan bilangan yang nggak bisa dinyatakan sebagai pecahan biasa. Sebagai desimal, bilangan ini juga nggak berhenti pada angka tertentu.

Contohnya seperti ini. Biasanya kita itu menyamakan π = 3,14 kan ya?  Tapi sebenarnya π itu desimalnya nggak habis. Nih sneak peek-nya.

Nah…

π=3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955082231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233…dan seterusnya…ngak kelar-kelar.

Lalu contoh lain misalnya.

√5=2.2360679774997896964091736687312762354406183596115257…

Apakah sobat Zenius udah kebayang apa itu bilangan rasional dan bilangan irasional? Kalo elo punya pertanyaan, langsung aja ya tanya di kolom komentar.

Sekarang kita lanjut ke pertidaksamaan rasional dan irasional.

Rumus Pertidaksamaan Rasional

Berikut ini bentuk bentuk umum pertidaksamaan rasional.

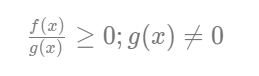
Nah, tadi kita udah sempat bahas ya kalau di pertidaksamaan itu terdapat berbagai notasi yang digunakan seperti < , >,  ≤, ≥, dan ≠.

Jadi, untuk pertidaksamaan rasional pun bentuk umum tadi tinggal diganti-ganti notasinya.

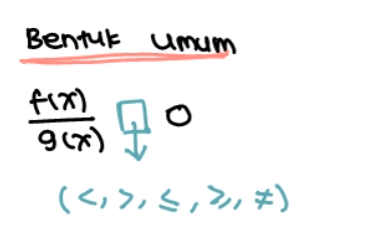
Contohnya kayak gini.

Oh iya sesuai bentuk umumnya, ruas kanannya harus 0 ya. Ini akan lebih elo pahami kalau sudah ketemu contoh soal pertidaksamaan rasional nanti.

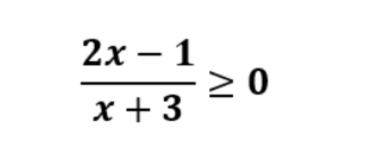
Perlu diketahui, bahwa pertidaksamaan rasional itu ada beberapa tipe, apa aja? Berikut ini tipe-tipe dan contohnya.

• Pertidaksamaan Rasional Linear

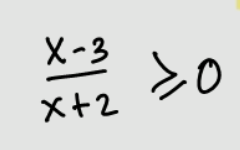
• Pertidaksamaan Rasional Kuadrat

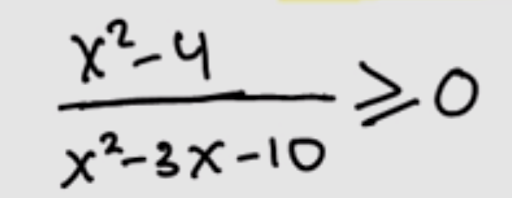
• Pertidaksamaan Rasional Mutlak

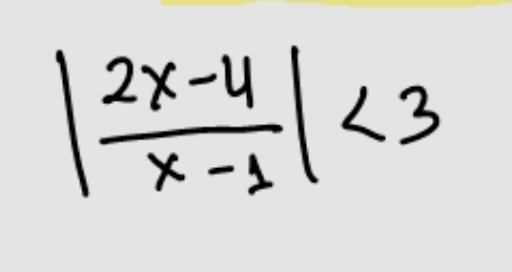
• Pertidaksamaan Rasional Linear-Kuadrat

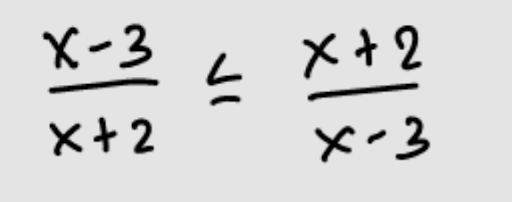
Lalu gimana penyelesaiannya? Sebenarnya karena tipe-tipe pertidaksamaan ini bermacam-macam, penyelesaiannya juga macam-macam.

Tapi ada beberapa tips yang bisa elo pegang ketika menyelesaikan pertidaksamaan-pertidaksamaan tersebut.

1. Ubah ke bentuk umum pertidaksamaan
2. Cari pembuat nol dari fungsi pembilang dan penyebut
3. Buat garis bilangan
4. Uji tanda untuk tiap daerah
5. Tentukan himpunan penyelesaian

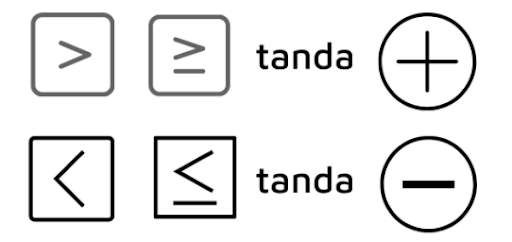
Daripada bingung-bingung, coba langsung ke contoh soal pertidaksamaan rasional dan irasional dulu ya.

Contoh Soal Pertidaksamaan Rasional

3x + 5x- 3 5

Tentukan himpunan penyelesaiannya.

Jawab: 

Nah, yuk kita coba ikuti step by step pengerjaannya.

Elo lihat kan, ruas kanannya masih 5 bukan 0. Sedangkan elo harus mengubahnya ke bentuk umum terlebih dulu, berarti angka 5 di kanan harus berubah jadi 0. 

Gimana caranya?  Ya tinggal elo kurang sama bilangan yang sama. Jangan lupa ruas kirinya juga ikut dikurang ya.

3x + 5x- 3 5 

3x + 5x- 3 – 55-5 

3x + 5x- 3 – 50       (Di sini udah dalam bentuk umum ya)

Biar bisa ngitung pengurangan 5 tentu harus disamakan ya penyebutnya, kayak di bawah ini:

3x + 5 – 5 (x-3)x- 3 0 

3x + 5 – 5x + 15x- 3 0 

-2x +  20x- 3 0 

Kalau sudah sampai sini langkah selanjutnya adalah mencari si pembuat 0 nya. Cara carinya tinggal pindah ruas aja ya, baik pembilang dan penyebut.

-2x + 20 = 0                                    x – 3 = 0

20 = 2x                                           x = 3

x = 10

Kalau sudah tahu x nya, tinggal dimasukin ke garis bilangan untuk uji tanda. 

Nah, dari garis bilangan elo bisa tahu mana yang positif dan negatif. Oh iya perlu diingat bentuk umum g(x) 0

g(x) kan merupakan penyebut tuh, jadi untuk menghitung x – 3 gak boleh pakai angka 3 ya, karena jika dimasukan ke x hasilnya akan 0. 

Setelah ditemukan tandanya, sekarang dimasukkan sesuai tandanya ya.

Jadi himpunan penyelesaiannya adalah x < 3 U x 10

Rumus Pertidaksamaan Irasional

Ini adalah bentuk umum pertidaksamaan irasional.

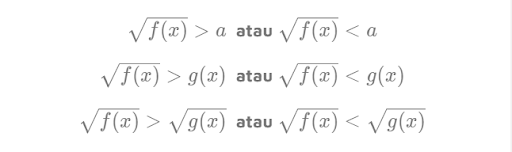
“Ingat ya, bilangan di bawah akar harus ≥0”

Dengan catatan, bilangan di dalam akar harus lebih dari atau sama dengan 0.

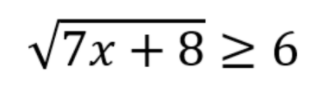
Nah, sekarang kita coba selesaikan contoh soal pertidaksamaan irasional di bawah ini bersama-sama ya.

Pertanyaannya, bener nggak sih himpunan penyelesaian dari pertidaksamaan di atas adalah X ≥4?

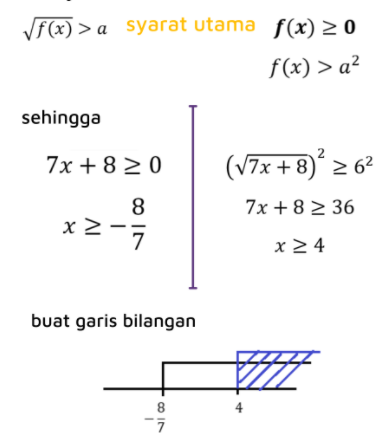
Coba lihat garis bilangannya deh yang di bagian bawah. Jadi benar atau nggak nih X ≥4? Jawab di kolom komentar ya!

Itu dia penjelasan singkat mengenai materi pertidaksamaan rasional dan irasional. Semoga lewat artikel di atas, elo jadi semakin memahami materi yang satu ini, ya!

Kalau elo masih belum jelas dan ingin mempelajari materi di atas lewat video pembelajaran, elo bisa banget mengaksesnya lewat Zenius.

Di video pembelajaran, ZenTutor mengemas materinya dengan menarik dan menambahkan contoh soal dan pembahasan di dalamnya sehingga mudah untuk mencernanya.

Klik banner di bawah ini buat aksesnya, ya!

Nggak cuman itu, elo juga bisa mengakses ribuan contoh soal dan pembahasan dari setiap mata pelajaran lainnya. Gimana, tuh, caranya? 

Sobat Zenius tinggal berlangganan paket Aktiva Sekolah dari Zenius! Lewat paket tersebut, elo bisa mengakses ribuan video premium dan berkesempatan ikut ujian try out sekolah.

Selain itu, elo juga bisa akses live class per minggu, lho! Menarik, kan? Yuk, klik banner di bawah ini buat berlangganan!

Selamat belajar, Sobat Zenius!

Baca Juga Artikel Lainnya:

Pengertian Elips Persamaan

Persamaan dan Pertidaksamaan Nilai Mutlak

Contoh Soal UTS Matematika Kelas 10

Originally published : November 6, 2021
Updated by Silvia Dwi & Maulana Adieb