Halo, Sobat Zenius! Lagi bingung tentang materi yang satu ini, ya? Tepat banget, nih, karena gue mau ngajak elo semua buat ngebahas materi fungsi kuadrat beserta contoh soal dan grafiknya!

Pembahasan rumus fungsi kuadrat dalam artikel ini akan dibatasi untuk materi SMP saja, ya, guys. Kenapa demikian? Karena materi kita kali ini masih satu pembahasan atau berkaitan dengan persamaan kuadrat.

Materi ini bisa dikatakan sebagai pengantar untuk materi fungsi kuadrat yang lebih luas pada saat Sobat Zenius memasuki jenjang SMA nanti.

Nah, sebelum masuk ke pembahasan rumus dan contoh fungsi kuadrat, kita mau ngomongin dulu, nih, mengenai pengertiannya. Check it out!

Daftar Isi

Pengertian dan Bentuk/Rumus Fungsi Kuadrat

Sebelum melangkah lebih jauh, mungkin Sobat Zenius masih belum paham apa yang dimaksud dengan fungsi kuadrat.

Fungsi kuadrat adalah fungsi polinomial yang memiliki variabel dengan pangkat tertinggi dua. Bentuk umum dari fungsi kuadrat menyerupai bentuk persamaan kuadrat.

Apakah Sobat Zenius masih ingat bagaimana bentuk persamaan kuadrat? Bentuknya seperti ini, guys, ax² + bx + c = 0. Nah, kalau bentuk umum fungsi kuadrat bagaimana? Hanya berbeda sedikit saja, nih, Sobat Zenius. Perhatikan di bawah ini.

f(x) = ax² + bx + c

f(x) = fungsi kuadrat

x = variabel

a, b = koefisien

c = konstanta

a ≠ 0

Fungsi Kuadrat dengan Tabel, Persamaan, dan Grafik

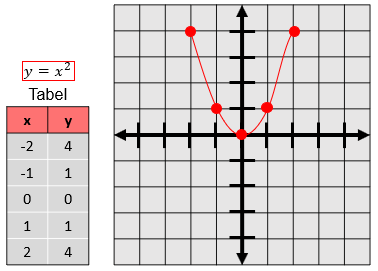
Pada submateri ini, kita akan membahas tentang bagaimana bentuk-bentuk dari fungsi kuadrat. Langsung saja, guys. Misal kita punya fungsi kuadrat y = x² dan ingin menggambar fungsi tersebut, kita akan membuat tabelnya terlebih dahulu.

Kita ambil contoh nilai-nilainya seperti pada contoh di bawah ini. Kemudian, tandai titik-titik potongnya dan kita dapati grafik fungsi kuadratnya. Catatan yang perlu diketahui Sobat Zenius, garis pada grafik tidak boleh tegak lurus karena akan membedakan nilai-nilai yang memenuhinya.

Sebelumnya kita sudah lihat grafik berdasarkan tabel, sekarang kita akan melihat grafik dari persamaan. Persamaan akan memudahkan menggambar titik potong x dan y.

Misalnya, kita punya persamaan y = x² + 2x +1, kita cari titik potong terhadap sumbunya.

Titik potong terhadap sumbu y

x = 0

y = 0² + 2(0) +1

y = 1

Titik potong (0, 1)

Titik potong terhadap sumbu x

x² + 2x +1 = 0

(x + 1)(x + 1) = 0

x = -1

Titik potong (-1, 0)

Setelah mengetahui nialinya, kita coba gambar grafiknya.

Hubungan antara Koefisien dengan Grafik Fungsi Kuadrat

Lanjut ke pembahasan selanjutnya yaitu mengenai materi grafik fungsi kuadrat dan hubungannya dengan koefisien.

Kita akan mencari tahu hubungan antara koefisien (a, b, dan c) dengan grafik.

Koefisien A

Langsung kita bahas koefisien a atau koefisien kuadrat. Misalnya kita punya y = x² + 1, y = -x² + 1, dan y = ½ x² + 1, maka grafiknya akan seperti pada berikut.

Kesimpulannya:

Jika a > 0, grafik terbuka ke atas
Jika a < 0, grafik terbuka ke bawah
Semakin besar nilai a, bentuk grafik semakin sempit

Koefisien B

Pada materi ini, diperlukan pengetahuan Sobat Zenius tentang melengkapkan kuadrat sempurna, ya.

Koefisien B disebut juga koefisien linear. Langsung saja, misalnya kita punya contoh persamaan y = x² + 2x + 4.

Kemudian, bentuk tersebut jika dilengkapi kuadrat sempurnanya akan menjadi (x + 1)² + 5, selanjutnya 1 kita sebut c dan 5 kita sebut d. Sebelumnya perlu elo ketahui dulu tentang ini.

Jika c positif, maka sumbu simetri x = -c, titik puncak (-c, d)
Jika c negatif, maka sumbu simetri x = c, titik puncak (c, d)

Kira-kira, grafiknya akan seperti berikut.

Konstanta C

Sekarang, kita bahas konstanta c terhadap grafik fungsi kuadrat. Konstanta c berpengaruh pada titik potong sumbu y.

Jika c semakin besar, semakin berada di atas
Jika c semakin kecil, semakin berada di bawah

Perhatikan grafik di bawah

Hubungan antara Diskriminan dengan Grafik Fungsi Kuadrat

Singkatnya, diskriminan adalah nilai yang dapat digunakan untuk menentukan banyaknya solusi persamaan kuadrat. Hubungannya apa dengan grafik fungsi kuadrat? Simak terus agar elo paham hubungan diskriminan dengan grafik fungsi kuadrat, ya.

Jika D > 0, akan ada 2 solusi real, atau grafik akan 2 kali menyentuh sumbu x.
Jika D = 0, akan ada 1 solusi real, atau grafik akan sekali menyentuh sumbu x.
Jika D < 0, tidak ada solusi real, atau grafik tidak akan menyentuh sumbu x.

Contohnya, kita punya fungsi y = 3x² + x + 1, berapa nilai diskriminannya?

D = b² – 4ac = 1² – 4(3)(1)= -11, berarti nilai D < 0, maka grafiknya seperti berikut.

Contoh Soal dan Pembahasan

Soal 1

Jika f(x) = x² – 4x, berapakah nilai dari f(2)?

Jawab:

f(2) = 2² – 4(2) = 4 – 8 = -4

Soal 2

Fungsi kuadrat yang memotong sumbu x di titik (3, 0) dan (-3, 0) melalui titik (0, -9) adalah …

Jawab

y = a(x – x₁)(x – x₂)

y = a(x + 3)(x – 3)

melalui titik (0, -9)

-9 = a(0 + 3)(0 – 3)

-9 = -9a

a = 1

y = 1(x + 3)(x – 3)

y = -9 + x²

Jadi, fungsi kuadrat tersebut adalah y = -9 + x².

Itu dia penjelasan singkat mengenai materi fungsi kuadrat dan grafiknya beserta contoh soal dan rumus-rumus dalam menyelesaikannya.

Jika Sobat Zenius ingin mendapatkan contoh soal yang lebih banyak lagi tentang fungsi kuadrat ataupun materi-materi TPS yang lainnya, elo bisa langsung klik banner di bawah ini!

Di sana, elo bisa belajar sepuasnya sampai yakin kalau udah siap menghadapi SNBT! Terus belajar dan berlatih agar dapat menguasai konsep dan materi kita kali ini. Biar makin mantap, Zenius juga punya beberapa paket belajar yang bisa lo pilih sesuai kebutuhan lo. Yuk langsung aja klik banner di bawah ini!