Pengertian postulat dalam matematika itu apa ya? Ternyata, mempelajari postulat itu penting banget buat elo yang ingin lolos UTBK. Karena, ada banyak soal sejenis ini yang muncul di UTBK.
Halo, Sobat Zenius! Nggak nyangka ya, sebentar lagi UTBK. Sudah mempersiapkan materinya belum? Salah satu tes yang ada di UTBK adalah TPS atau Tes Potensi Skolastik, yaitu untuk mengukur kemampuan kognitif berupa penalaran dan pemahaman umum.
Buat yang mengira kalau TPS ini nggak ada perhitungan atau kuantitatifnya, kali ini elo kurang tepat. Karena, salah satu sub-tes pada TPS adalah pengetahuan kuantitatif yang mencakup logika, kalkulus, peluang, statistika, dan geometri.
Nah, salah satu jenis soal logika yang tampil pada soal TPS PK adalah postulat dasar matematika. Hmm … Itu apaan ya? Apa sih pengertian postulat dalam matematika? Gimana sih contoh postulat? Penasaran? Langsung aja deh kita bahas, yuk!

Daftar Isi
Pengertian Postulat
Apa itu postulat? Kalau kita artikan secara bahasa, pengertian postulat adalah asumsi atau pernyataan yang dianggap benar dan nggak perlu bukti. Istilah ini juga seringkali dikenal sebagai aksioma, yaitu suatu pernyataan yang bisa diterima sebagai kebenaran tanpa pembuktian.
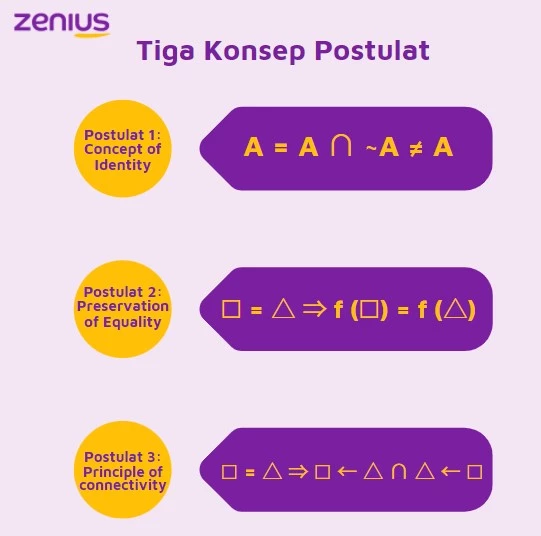
Kali ini, gue akan mengajak elo untuk mempelajari postulat sama dengan (=) atau postulate on equality. Ada berapa sih postulat dasar matematika? Kita sering menggunakan ketiga postulat, yaitu concept of identity, preservation of equality, dan principle of connectivity.
Baca juga: Logika Matematika – Konjungsi, Disjungsi, Implikasi, dan Biimplikasi
Postulat 1: Concept of Identity
Konsep dari pengertian postulat yang pertama ini merupakan kesamaan dari substitusi dan formasi. Analoginya gini, ketika dia A, maka dia akan sama dengan A. Kalau dia bukan A, maka dia tidak akan sama dengan A. Kalau dituliskan dalam bentuk matematis, maka akan seperti ini.
A = A ∩ ~A ≠ A
Oke, supaya makin jelas, kita ambil contoh postulat dalam matematika berdasarkan kesamaan substansinya berikut ini.
x + x = 2x
Hasilnya sama atau beda? Dilihat dari substansinya, antara x + x dan 2x itu memiliki nilai yang sama.
Contoh lainnya pada 7 – 4 = 6 – 3. Hasilnya sama-sama 3, kan? Intinya, ketika berbicara substansi, maka isinya harus sama. Lalu, bagaimana dengan kesamaan formasi? Coba elo perhatikan bentuk matematika di bawah ini!
ax2 + bx + c = 0
x2 + 2x + 4 = 0
Bentuk kuadrat di atas termasuk dalam postulat 1 atau bukan? Termasuk ya, guys. Karena, bentuk kuadrat di atas memiliki kesamaan formasi. Kita jadi bisa tahu nih, kalau a = 1, b = 2, dan c = 4.
Formasi inilah yang nantinya akan digunakan untuk menerapkan formula-formula di matematika. Contohnya pada saat elo menghitung Sn aritmatika dan mencari gradien suatu garis. Elo bisa lihat contoh perhitungannya di sini.
Baca juga: Konsep, Grafik, & Rumus Fungsi Kuadrat
Postulat 2: Preservation of Equality
Konsep yang kedua ini yaitu tentang bagaimana cara elo mempertahankan sama dengan. Analoginya gini, ketika elo punya kotak yang sama dengan segitiga, maka apa yang elo lakukan terhadap kotak harus sama dengan apa yang elo lakukan terhadap segitiga.
☐ = △ ⇒ f (☐) = f (△)
Nah, postulat 2 ini umumnya digunakan untuk dasar-dasar aljabar. Contohnya, x = a, maka x + 2 = a + 2. Begitu juga dengan 2x = 2a.
Intinya, selama proses yang elo lakuin sama, maka hasilnya juga akan sama. Syaratnya, nggak boleh dibagi atau dikali dengan 0.
Aplikasi dari postulat 2, yaitu ketika elo menemukan ada soal dengan tipe seperti ini, “Diketahui suatu fungsi aljabar 2x – 5 = 12. Berapa nilai x?”
Solusi:
2x – 5 = 12
2x = 12 + 5
2x = 17
x = 17/2.
Jadi, nilai x adalah 17/2.
Baca juga: Sifat & Rumus Integral Tak Tentu – Materi Matematika Kelas 11
Postulat 3: Principle of connectivity/replaceability
Di dalam matematika, semuanya bisa nyambung atau connect satu sama lain. Kenapa? Kita pakai analogi gini, ketika kotak sama dengan segitiga, maka kotak tersebut bisa diganti dengan segitiga. Begitu pun sebaliknya.
☐ = △ ⇒ ☐ ← △ ∩ △ ← ☐
Misalnya, elo punya template sin (a±b) = sin a sin b ± sin b sin a dan cos (a±b) = cos a cos b ∓ sin a sin b. Gimana cara perhitungannya menggunakan postulat?
Kita ambil contoh dulu nih, ceritanya kita mau cari tahu nilai dari sin 2x.
Sin 2x = sin (x+x) = sin x cos x + sin x cos x = 2 sin x cos x.
Udah deh, yang penting elo ikutin aja formatnya. Masih penasaran? Oke, kita cari tahu berapakah nilai cos 2x?
Cos 2x = cos (x+x) = cos x cos x – sin x sin x = cos2 x = sin2 x = cos2 x – (1 – cos2 x) = 2 cos2 x – 1 (ini gue udah menggunakan postulat 3, yaitu mengubah nilai sin2 x = 1 – cos2 x.
Uraian di atas bisa elo pelajari menggunakan video belajar Zenius dengan klik banner di bawah ini.
Contoh Soal dan Pembahasan Pengertian Postulat
Untuk menguji sejauh mana pemahaman elo mengenai materi pengertian postulat dan contohnya, gue ada beberapa contoh soal dan pembahasan yang bisa dijadikan sebagai referensi.

Contoh Soal 1
Jawab: .
Pembahasan: Elo perlu paham dulu mengenai integral. Ada aturan yang sesuai dengan postulat 1, yaitu sebagai berikut.
, dengan catatan n ≠ -1.
Contoh Soal 2
Diketahui suatu fungsi 3x = 32x-1. Tentukan nilai x!
Jawab: x = 1.
Pembahasan: Ketika bertemu soal seperti ini, elo jangan panik dulu. Elo lihat lagi, kira-kira bisa pakai postulat yang mana nih? Kita pakai kotak pada x dan segitiga pada 2x-1. Kita bisa menggunakan postulat seperti ini:
x = 2x – 1
x + 1 = 2x
1 = 2x – x
1 = x
Jadi, nilai x adalah 1.
Contoh Soal 3
Suatu fungsi kuadrat y = ax2 + bx + c. Tentukan nilai x! (dengan nilai xmaks = ).
Kali ini gue nggak akan menampilkan pembahasannya, karena gue mau elo coba kerjakan sendiri. Itung-itung latihan soal gitu, guys. Kalau elo masih bingung, elo bisa cek pembahasannya di sini.
*****
Gimana nih, sampai sini udah paham kan tentang pengertian postulat? Buat yang lebih menyukai belajar dengan nonton video, elo bisa mengakses materi UTBK lainnya di video Zenius. Elo juga bisa mencoba melatih kemampuan dengan level soal yang mirip UTBK beneran di Try Out bareng Zenius.
Baca juga: Materi dan Contoh Soal Pengetahuan Kuantitatif – TPS UTBK










Leave a Comment