Artikel ini akan membahas tentang invers matriks yang termasuk dalam materi pelajaran Matematika Wajib Kelas 11.

Elo tau nggak kalau sebuah angka ternyata punya nilai opposite atau kebalikan? Iya, itu yang dinamakan dengan invers. Di artikel ini gue mau ajak elo belajar tentang cara mencari invers matriks 2×2 dan 3×3 dengan rumus invers matriks.

Sebelum masuk ke cara mencari invers matriks, pembahasan serta contoh soal invers matriks, elo perlu paham konsep invers dulu. Gimana sih taunya sebuah nilai punya kebalikan?

Gini nih misalnya angka 2, kebalikan dari angka 2 adalah atau bisa ditulis dengan 2-1. Kebalikan dari angka 15 berarti atau 15-1. Nah, sekarang kalau angkanya adalah pecahan, nilai kebalikannya gimana? Gak usah bingung, tinggal dibalik aja.

Misalnya pecahan berarti kebalikannya adalah 5 atau -1. Kita bisa menyebut kebalikan atau opposite dengan istilah invers.

Lalu, apakah invers berlaku juga pada matriks? Yap, tentu saja berlaku. Di materi pelajaran Matematika Wajib kelas 11, elo udah belajar tentang matriks dan determinan matriks, iya kan?

Kalau mau mengingat dan butuh review lagi, elo bisa langsung meluncur ke artikel yang udah gue tulis sebelumnya.

Baca Juga: Matriks Matematika Itu Apa Sih?

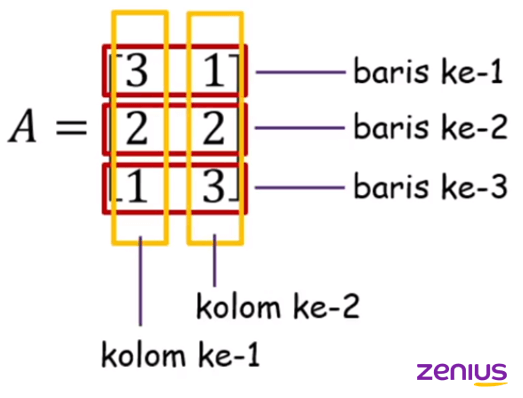
Review sedikit, yuk! Matriks adalah susunan persegi/persegi panjang yang terdiri dari angka dan diatur dalam baris dan kolom. Masih ingat kan kalau baris itu yang susunannya horizontal (kanan-kiri), sedangkan kolom yang susunannya vertikal (atas-bawah) seperti ini.

matriks matematika baris dan kolom zenius — Materi Matriks (Arsip Zenius)

Daftar Isi

Cara Mencari Invers Matriks?

Nah, kita nyambung lagi ke invers matriks. Suatu matriks juga memiliki invers. Konsepnya masih sama, bahwa ketika ada matriks A, maka inversnya adalah A-1.

Selain konsep tersebut, untuk mencari invers matriks juga ada konsep lainnya yang harus elo perhatikan.

Ketika kita mengalikan suatu angka dengan kebalikannya, maka hasilnya akan bernilai 1.

$Perhitungan Invers Matriks 2x2 dan 3x3 177$

Ketika dibalik hasilnya juga akan tetap sama, yaitu 1.

$Perhitungan Invers Matriks 2x2 dan 3x3 178$

Hal yang sama juga berlaku pada matriks. Ketika kita mengalikan matriks dengan kebalikannya, maka kita akan mendapatkan matriks identitas (yang setara dengan nilai 1).

$Perhitungan Invers Matriks 2x2 dan 3x3 179$

Begitu pun dengan kebalikannya.

$Perhitungan Invers Matriks 2x2 dan 3x3 180$

Elo masih ingat gak matriks identitas itu yang seperti apa? Yap, matriks persegi yang semua elemen diagonal utamanya bernilai satu, sedangkan elemen lainnya bernilai nol. Seperti ini ilustrasinya.

Sebelum memasuki invers matriks, ada baiknya elo kenal dulu sama istilah determinan, minor-kofaktor, dan jenis-jenis matriks. Gue udah pernah nulis artikel yang membahas poin-poin tersebut di artikel gue yang ini.

Invers matriks persegi ada yang memiliki ordo 2×2 dan 3×3. Dari kedua matriks persegi ini elo bisa mencari determinannya untuk bisa mencari invers matriks.

Invers Matriks 2×2

Menghitung invers matriks ordo 2×2 lebih mudah dibandingkan dengan matriks yang berordo lebih tinggi seperti 3×3. Elo hanya perlu menghitungnya menggunakan rumus di bawah ini.

Rumus Invers Matriks 2×2

$Perhitungan Invers Matriks 2x2 dan 3x3 182$

Kalau elo bertanya, Adj A itu apa sih? Jadi, Adj A adalah adjoin matriks A, berarti transpose dari matriks A yang elemen-elemennya merupakan kofaktor dari elemen-elemen matriks A.

Untuk mengetahui kofaktor itu yang gimana, elo bisa baca lagi artikel gue sebelumnya tentang Determinan Matriks.

Contohnya gini, ada suatu matriks $Perhitungan Invers Matriks 2x2 dan 3x3 183$ . Elo diminta untuk mencari invers dari matriks A tersebut. Elo bisa masukan matriks A ini ke dalam rumus di atas, seperti ini:

$Perhitungan Invers Matriks 2x2 dan 3x3 184$

|A| ini lambang apa sih? Ini determinan matriks ya. Jadi elo tinggal menggali silangkan elemen-elemen secara diagonal untuk tau determinannya.

Makanya, di rumus didapatkan ad – bc ya. Huruf-huruf itu tinggal elo ganti ke angka nanti di contoh soal invers matriks 2×2.

Nah, jadi untuk mendapatkan adjoin dari matriks A yang ordonya 2×2, elo hanya perlu menukar posisi a dan d, kemudian letakkan nilai negatif di depan b dan c.

Contoh Soal Invers Matriks Ordo 2×2 dan Jawabannya

Untuk mempermudah, kita langsung cemplungin angka-angkanya ke dalem, yuk! Perhatikan contoh soal di bawah ini!

$Perhitungan Invers Matriks 2x2 dan 3x3 185$

Dari soal di atas udah diketahui tuh determinannya. Selanjutnya, kita hitung invers dari matriks P-nya atau P-1.

$Perhitungan Invers Matriks 2x2 dan 3x3 186$

Nah, sekarang elo udah menemukan invers dari matriks P. Untuk membuktikan apakah hasil tersebut benar, elo bisa pakai konsep yang pertama gue tulis di atas bahwa AxA^-1= I (matriks identitas). Langsung aja deh kita buktikan.

$Perhitungan Invers Matriks 2x2 dan 3x3 187$

$Perhitungan Invers Matriks 2x2 dan 3x3 188$

Untuk membuktikan persamaan selanjutnya, coba deh elo hitung apakah A^-1A=I juga?

Dari hasil perhitungan di atas, elo udah paham mulai dari konsep, cara mencari invers matriks 2×2, hingga membuktikan bahwa hasil tersebut sudah benar.

Invers Matriks 3×3

Sekarang kita masuk ke invers matriks ordo 3×3, gimana sih cara perhitungannya? Apakah sama dengan matriks berordo 2×2?

Sebenarnya, untuk menentukan invers dari matriks berordo 3×3 itu bisa dilakukan dengan beberapa cara, ada yang menggunakan metode Eliminasi Gauss-Jordan atau transformasi baris elementer dan menggunakan adjoin.

Kali ini, gue bakal membahas perhitungan invers dengan Adjoin sama seperti matriks berordo 2×2. Apakah cara perhitungannya sama? Oke, langsung aja kita bahas deh biar tau caranya sama atau berbeda.

$Perhitungan Invers Matriks 2x2 dan 3x3 189$

Secara umum, rumus invers matriks adalah $Perhitungan Invers Matriks 2x2 dan 3x3 190$ .

Jadi rumus invers matriks 3×3 tetap menggunakan rumus umum tersebut ya.

Nah, untuk menentukan determinan matriks 3×3, kita bisa menggunakan dua cara, yaitu metode Sarrus dan Minor-Kofaktor.

Lalu, gimana cara menentukan Adjoin matriks 3×3? Elo harus ingat cara menentukan kofaktor matriks a_ij, yaitu C_ij = (-1)^i+jM_ij, di mana M_ij adalah minor dari matriks A_ij, sedangkan C_ij adalah kofaktor A atau Kof(A).

$Perhitungan Invers Matriks 2x2 dan 3x3 191$

Berarti, C₁₁ = (-1)¹⁺¹M₁₁=M₁₁ , C₁₂= (-1)¹⁺²M₁₂= –M₁₂ , dst sampai dihasilkan seperti ini.

$Perhitungan Invers Matriks 2x2 dan 3x3 192$

Selanjutnya kita cari determinannya, dengan cara M_ij = det(A_ij). Misalnya kita ambil contoh M₁₁ = det(A₁₁) = $Perhitungan Invers Matriks 2x2 dan 3x3 193$ (menghilangkan elemen baris ke-1 dan kolom ke-1, sehingga hanya diperoleh ordo 2×2 untuk setiap elemennya), dst sehingga diperoleh seperti ini.

$Perhitungan Invers Matriks 2x2 dan 3x3 194$

Balik lagi, tujuan kita adalah untuk mencari Adjoin matriks A. Apa sih hubungannya dengan kofaktor? Kenapa kita perlu mencari kofaktor terlebih dahulu?

Ternyata, hubungannya adalah Adjoin matriks A sama dengan transpose dari matriks A atau disimbolkan seperti ini: Adj(A) = Kof(A)^t.

Masih ingat kan transpose itu apa? Yap, elemen-elemen pada baris diganti jadi kolom, dan elemen kolom diganti jadi baris.

Contoh Soal Invers Matriks 3×3 dan Jawabannya

Supaya gak makin bingung, kita langsung cemplungin ke dalam angka-angka ya.

Coba perhatikan kutipan video materi dari Zenius yang membahas Contoh Soal Tentang Invers Matriks 3×3 dengan Adjoin di bawah ini.

Contoh Soal Invers Matriks 3x3 dengan Adjoin Zenius — Video Materi Premium Zenius tentang Contoh Soal Invers dari Matriks 3×3 dengan Adjoin

Nah, dari situ, kita lanjut tentukan transpose dari Kof(A) untuk menentukan Adj(A).

$Perhitungan Invers Matriks 2x2 dan 3x3 196$

Sekarang kita masukkan rumusnya:

$Perhitungan Invers Matriks 2x2 dan 3x3 197$

Gimana, lebih gampang setelah dimasukkan angka-angkanya kan? Dari penjelasan di atas tentang invers dari matriks 3×3, elo udah tau nih metode apa aja yang bisa elo gunakan, cara menentukan determinan dan Adjoin, dan cara perhitungan invers matriks berordo 3×3.

Materi ini mungkin masuk dalam TPS (Tes Potensi Skolastik) dalam UTBK, lho. Makanya gak ada salahnya untuk benar-benar paham tentang materi invers matriks yang satu ini.

Biar makin paham elo bisa cek materi belajar di banner bawah ini dengan penjelasan dan latihan soal yang lebih banyak lagi. Jangan lupa login atau daftar dulu biar punya akun Zenius. Abis itu tinggal elo ketik topik materi yang mau dipelajari di kolom pencarian.

Perhitungan Invers Matriks 2x2 dan 3x3 198 — Klik banner di atas!

Oke, sampai sini dulu deh penjelasan mengenai invers matriks. Semoga apa yang udah gue sampaikan di atas bisa memudahkan proses belajar dan mengerjakan tugas.

Kalau elo masih bingung, langsung bilang di kolom komentar bagian mana yang masih elo kurang paham ya!

O ya, gue juga mau rekomendasiin paket belajar dari Zenius buat elo yang duduk di kelas 10, 11, dan 12 SMA. Melalui paket ini elo bisa akses ke ribuan video materi belajar, latihan soal, tryout, dan sesi live class buat bantu ningkatin nilai rapor elo. Cek info selengkapnya dengan klik banner di bawah ya!