Hi, Sobat Zenius! Kali ini, gue mau bahas materi rumus persamaan trigonometri. Pada artikel sebelumnya, elo mungkin sudah pernah melihat persamaan trigonometri. Namun, materi yang disampaikan di sana tidak terlalu mendalam, sehingga Sobat Zenius mungkin masih kesulitan untuk memahami konsep tersebut.

Nah, artikel ini hadir untuk memberikan pemahaman lebih mendalam tentang konsep dan rumus persamaan trigonometri. Coba Sobat Zenius perhatikan baik-baik, ya, materi yang akan disampaikan sekarang.

Daftar Isi

Apa yang Dimaksud Persamaan Trigonometri?

Persamaan trigonometri adalah persamaan yang memuat fungsi trigonometri. Contohnya seperti berikut.

sin (x) = 0
sin (x) = cos (x)
sin (x) = tan (x)

Dari ketiga contoh tersebut, kita dapat melihat bahwa setiap persamaan yang ada di atas itu memuat fungsi trigonometri. Jadi, kalau kita ketemu dengan persamaan yang memuat fungsi trigonometri saja, kita dapat menyebutnya persamaan trigonometri. Namun, jika memuat fungsi lainnya, seperti fungsi aljabar dan fungsi logaritma, kita tidak dapat menyebutnya fungsi trigonometri.

Ada dua solusi untuk mencari solusi dari persamaan trigonometri, yaitu solusi prinsipal dan solusi umum.

Rumus Persamaan Trigonometri

Solusi Prinsipal

Solusi prinsipal persamaan trigonometri adalah himpunan solusi yang memenuhi persamaan trigonometri dan terletak pada interval (0, 2𝜋)

Kita punya contoh persamaan trigonometri, misalnya cos (x) = 1. Sobat Zenius masih ingat kan, pada materi sebelumnya, kita sudah belajar sudut apa yang membuat nilai cos bernilai 1. Ada x = 0 dan ada x = 360º.

Dari kedua angka 0 dan 360º, manakah yang merupakan solusi prinsipal? Sudah jelas angka yang pertama, yaitu 0. Kenapa begitu? Karena 0 terletak pada (0, 2𝜋). Meskipun 2𝜋 = 360º, 360º tidak termasuk karena memiliki nilai sama dengan batas atas. Berarti prinsip prinsipal dari cos (x) = 1, hanya x = 0.

Sekarang kita coba contoh kedua menggunakan grafik.

Contoh kedua, kita mencari solusi sin (x) = ½ dari fungsi f(x) = sin (x). Fungsi tersebut akan berulang atau periodik seperti pada grafik selama periode 2𝜋.

½ terletak pada sumbu Y, dari angka tersebut dapat dibuat garis putus-putus. Pada grafik, garis putus-putus tersebut diberi warna merah.

Lalu, solusi dari sin (x) = ½ itu adalah titik potong grafik sin (x) dengan garis merah putus-putus atau Y. Titik tersebut diberi warna merah pada grafik.

Kemudian, karena kita fokus pada pencarian solusi prinsipal, kita batasi pada interval 0 sampai 2𝜋. Batas itu diberi warna kuning pada grafik.

Jika dilihat, titik potong yang berada pada interval adalah x₁ dan x₂. Titik potong yang lainnya, berada di luar interval 0 sampai 2𝜋.

Anggaplah misalkan x₁ dan x₂ memiliki nilai sin 30º dan sin 150º, maka nilai x₁ dan x₂ seperti dalam grafik. Jika elo belum paham tentang derajat dan radian, elo bisa review kembali materi tersebut di sini. Kalau begitu solusi prinsipal dari sin (x) = ½ adalah sebagai grafik berikut.

Oya, elo udah install aplikasi Zenius belum? Biar pemahaman elo lebih mateng di materi ini dan di pelajaran lain, elo bisa manfaatin berbagai fitur di aplikasi Zenius. Banyak yang gratis, lho. Download dengan klik banner di bawah ini ya!

Download Aplikasi Zenius

Fokus UTBK untuk kejar kampus impian? Persiapin diri elo lewat pembahasan video materi, ribuan contoh soal, dan kumpulan try out di Zenius!

Solusi Umum

Solusi umum dari persamaan trigonometri sebenarnya ada banyak. Kenapa bisa banyak, guys? Kita tahu bahwa fungsi trigonometri adalah fungsi yang periodik. Contohnya seperti pada persamaan dan grafik berikut.

X-nya ada banyak, itulah mengapa disebut solusi umum. Solusi umum dari persamaan trigonometri berupa himpunan nilai yang memenuhi persamaan tersebut.

Solusi umum sin x = sin 𝛼

Seperti yang sudah dikatakan sebelumnya, fungsi dari solusi umum sin adalah fungsi yang periodik. Jadi, bagaimana tuh?

Begini Sobat Zenius, misalkan kita memiliki suatu persamaan sin x = sin 30º. Lalu, sin 30º itu berapa sih? ½ kan? Iya, dong! Coba ingat-ingat lagi sudut istimewa.

Jadi, x-nya tuh berapa?

x = 30º,

x = 150º,

x = 30º + 360º,

x = 150º + 360º, dan seterusnya.

Ini menunjukkan bahwa fungsi ini periodik. Dengan demikian, kita ketahui bahwa solusi dari sin x = sin 30º ada sangat banyak. Di sini, kita akan mencari solusi umumnya, karena tidak akan ada habisnya dan tidak mungkin kita mencari satu-satu nilai x seperti di atas.

Pertanyaannya adalah ada gak sih suatu bentuk umum yang bisa menyatakan solusi dari x-nya? Langsung aja simak grafik f(x) = sin (x) di bawah.

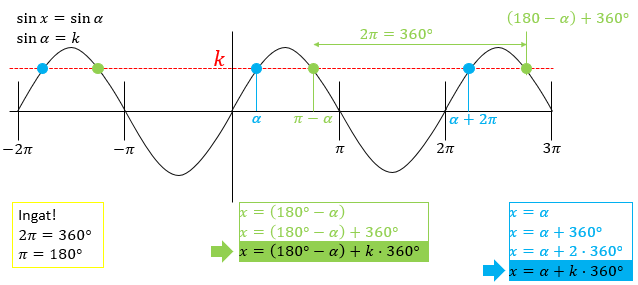
Yap, solusi umum dari persamaan trigonometri dinyatakan pada bentuk yang ditunjuk oleh anak panah hijau dan biru. Grafiknya membentuk bukit dan lembah dengan K adalah bilangan bulat dan 360º juga dapat diubah bentuknya menjadi 2𝜋.

Solusi umum cos x = cos 𝛼

Bagaimana cara mencari solusi umum dari persamaan cos x = cos 𝛼? Kita akan jawab menggunakan grafik, tetapi Sobat Zenius harus tahu kalau solusi umum cos juga bersifat periodik.

Grafik pada fungsi cos juga akan membentuk bukit dan lembah. Perbedaannya terletak pada awal mulainya. Satu periode pada fungsi sin x dimulai dari 0 (nol) dan kembali ke 0 (nol), sedangkan pada satu periode fungsi cos x dimulai dari 1 (satu) dan kembali ke 1 (satu).

Perhatikan grafik di bawah, ya!

Solusi umum tan x = tan 𝛼

Sekarang kita bahas solusi umum dari persamaan tan x = tan 𝛼. Grafik fungsi tan memiliki perbedaan dengan grafik fungsi sin dan cos. Grafik fungsi tan tidak membentuk bukit dan lembah. Hal ini disebabkan oleh nilai tan yang tidak terdefinisi pada sudut 90º dan 270º, sehingga dalam rentang 0º sampai 360º terdapat dua buah asimtot.

Perhatikan grafik di bawah!

Tips & Trik

Sederhanakan persamaan trigonometri menggunakan identitas-identitas trigonometri dan manipulasi aljabar sehingga berbentuk setidaknya sin (x) = K, cos (x) = K, atau tan (x) = K.
Cari solusi dari sin (x) = K, cos (x) = K, atau tan (x) = K pada interval $Rumus Persamaan Trigonometri dan 2 Solusinya 9$ .
Gunakan solusi umum untuk mencari semua solusi.
Pilih solusi yang sesuai dengan interval solusi pada soal (opsional).

Soal dan Pembahasan

Banyaknya x yang memenuhi 2sin² (2x) – 14sin x cos x + 3 = 0 pada interval -𝜋 ≤ x ≤ 𝜋 adalah ….

Jawab:

2sin² 2x – 14sin x cos x + 3 = 0

2sin² 2x – 7sin 2x + 3 = 0

Bisa dibuat menjadi persamaan kuadrat

2p² – 7p + 3 = 0

(2p – 1)(p – 3) = 0

p = 3

p = ½

Fungsi sin tidak mungkin lebih dari 1, maka pilih p = ½

Coba cari nilai sin 2x = ½

sin 2x = ½ = sin 30º

sin x = sin 𝛼

x = 𝛼 + 360k

x = (180 – 𝛼) + 360k

sin 2x = sin 30º

2x = 30º + 360k

x = 15º + 180k

x = {-165, 15, 195, …}

2x = 150º + 360k

x = 75º + 180k

x = {-105, 75, 255, …}

Jadi, banyaknya x adalah 4, yaitu {-165, -105, 15, 75}.

Oke, sekian rangkuman persamaan trigonometri ini, semoga kalian dapat memahami materi ini dengan baik. Pahami konsepnya dan terus berlatih soal serta daftar paket belajar Zenius Aktiva Sekolah yuk. Elo bisa dapet akses ke ribuan materi soal, tryout premium, ikut live class, dan study guide per semester. Cari tahu info selengkapnya dengan klik banner di bawah ini ya, Sobat Zenius. Sampai bertemu pada materi lainnya, ya!