Bingung dengan soal-soal pembagian suku dalam matematika? Gampang banget kok caranya, semua dijelaskan secara sederhana di sini, lengkap dengan contoh soal.
[latexpage]
Pernah kepikiran nggak sih kalau konsep pembagian pada suku banyak ini sama dengan konsep pembagian pada bilangan bulat yang pernah kita pelajari waktu SD? Coba kita inget-inget lagi nih ya konsep pembagian pada bilangan bulat. Misalnya….
Kalau kita bagi bilangan 261 dengan 7, berapa hasilnya? Berapa sisanya?
Kalau soalnya kaya yang di atas ini pasti bisa dong ngerjainnya. Anak SD juga bisa 🙂 . Kita pakai pembagian bersusun aja ya, kaya gini:
Dari sini juga ketahuan kalau hasil baginya 37 dan sisa baginya 2. Kalau gitu, kita bisa tulis pembagian tersebut begini kan:
$$ \frac{261}{7} = 37 + \frac{2}{7} $$
Nah, terus ruas kiri dan ruas kanan kita kali dengan 7, sehingga persamaannya begini:
$$ 261 = 37.7 + 2 $$
[Btw, udah tau kan kalau ruas kiri dan ruas kanan boleh dikaliin dengan 7 kaya contoh di atas? Ini konsep aljabar yang penting buanget di matematika. Konsep pindah ruas (tambah pindah ruas jadi kurang, bagi pindah ruas jadi kali, dsb) datangnya dari sini. Penting banget sih lo kuasain konsep aljabar yang satu ini. Coba deh tonton video sabda tentang postulat dasar matematika.]
Okay.. kita lanjut lagi. Jadi kalau kita punya 4 bilangan berikut ini:
- Bilangan yang akan dibagi (contoh di atas = 261)
- Bilangan pembagi (contoh di atas = 7)
- Bilangan hasil bagi (contoh di atas = 37)
- Bilangan sisa (contoh di atas = 2)
Kita bisa bikin hubungan kaya gini:
Bilangan yang akan dibagi = (bilangan pembagi) x (bilangan hasil bagi) + bilangan sisa
Nah, kalau kita pakai konsep ini untuk mengerjakan pembagian pada suku banyak, harusnya sama aja dong. Coba misalnya kita punya suku banyak gini:
$$ x^3-x^2+x-1 $$
Terus, kita mau coba bagi suku banyak ini dengan $ (x-2) $. Kira-kira gimana hasil dan sisanya? Kita bagi pakai pembagian bersusun lagi deh (ceritanya belum tau tentang Horner dan Teorema sisa, jadi pakai ini dulu).
Kelihatan kan kalau hasil baginya adalah $ x^2 + x + 3 $ dan sisanya adalah $ 5 $. Kalau gitu, hubungan antar sukubanyak itu bisa kita tulis jadi:
$$ \frac{x^3-x^2+x-1}{x-2} = (x^2 + x + 3) + \frac{5}{x-2} $$
Kedua ruas kita kaliin dengan $ (x-2) $ sehingga menjadi
$$ x^3-x^2+x-1 = (x^2 + x + 3)(x-2) + 5 $$
Kelihatannya aja ribet. Padahal sama aja polanya sama pembagian bilangan yang kita pelajari waktu SD. Makanya rumusnya juga sama kalau kita ambil empat sukubanyak gini:
- $ P(x) $ = Sukubanyak yang akan dibagi $(x^3-x^2+x-1)$
- $ Q(x) $ = Sukubanyak pembagi $(x-2)$
- $ H(x) $ = Sukubanyak hasil bagi $ (x^2 + x + 3) $
- $ S $ = Sukubanyak sisa $ (5) $
Persamaannya sama aja:
$$ P(x) = H(x).Q(x) + S $$
Atau kalau $ Q(x) = x-h $, kita bisa tulis persamaannya menjadi
$$ P(x) = H(x).(x-h) + S $$
Daftar Isi
TEOREMA SISA
Kalau lo udah bener-bener ngerti persamaan di atas, baru deh gampang banget untuk bisa mengerti konsep teorema sisa. Bunyi salah satu teorema sisa tuh gini:
Sukubanyak P(x) jika dibagi dengan (x-h) maka sisanya adalah P(h)
Ya iya lah… coba aja masukin nilai $ x = h $ di persamaan (1), hasilnya pasti gini:
$$ P(h) = H(h).(h-h) + S $$
$$ P(h) = H(h).0 + S $$
$$ P(h) = S $$
Kalau udah tau konsepnya, kita nggak perlu heran kalau sisa pembagian terhadap $ (x-h) $ adalah $ P(h) $. Tinggal masukin (substitusi) aja.
Sedikit tips
Nah, dari tulisan ini, ada selipan tips sedikit. Pertama, jangan lupain fundamental skills di matematika, termasuk fundamental skills yang pernah lo pelajarin waktu SD dan SMP. Banyak banget fundamental skills di matematika yang akan dipake ketika lo mempelajari berbagai macam bab matematika lainnya. Tapi jangan khawatir. Lo nggak perlu buka-buka buku SD dan SMP lagi untuk ngecek fundamental skills apa aja yang mungkin lo masih kurang. Kita udah rangkum ini di beberapa video kita kok. Contohnya di Postulat Dasar dan Basic Mathematical Skills. Btw, fundamental skills ini juga suka muncul ketika lo mempelajari ilmu lain, termasuk Fisika, Kimia, Biologi, Ekonomi, bahkan Psikologi sekalipun.
Kedua, kalau lihat persamaan yang ribet, jangan takut duluan. Kebanyakan persamaan atau rumus-rumus itu sebenernya bisa dilihat dari cara yang simple. Contohnya konsep pembagian sukubanyak yang di atas.
Suku banyak – Practice, practice, practice…
Konsep suku banyak yang dijabarin di atas tentunya baru permulaan aja. Untuk belajar konsep suku banyak selengkapnya, bagusnya lo tonton juga video suku banyak di sini:
Seperti biasa, di kedua link itu ada video teori, ada latihan soal, dan ada video pembahasannya juga. Coba terapin aja konsep yang lo pelajari di sini di berbagai soal yang ada di link itu.
—————————CATATAN EDITOR—————————
Buat yang mau nanya atau ngobrol dengan Wisnu, langsung aja comment di bawah artikel ini. Kalo kamu belum gabung dengan Zenius, pastiin kamu gabung dengan kita dengan sign up zenius.net








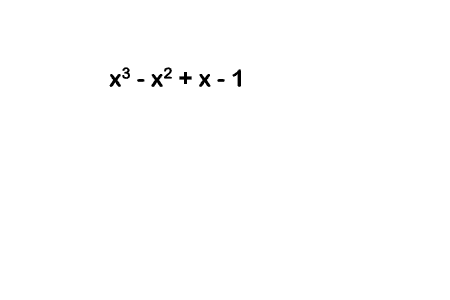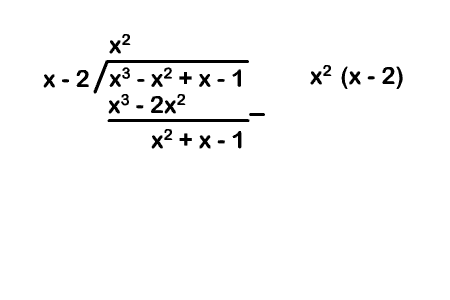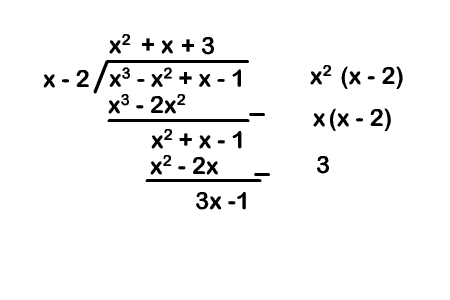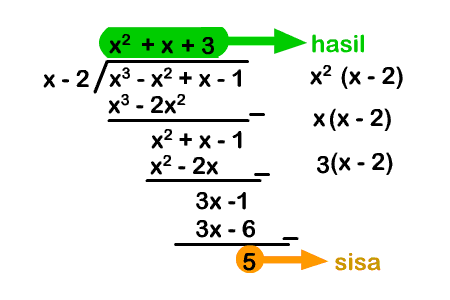

Sorry OOT nih , mau nanya saya tuh mau ngisi voucher yang udah abis , nah kalo lewat indomart ribet kayaknya , mau tanya kalo outlet zenius di deket bandung disebelah mananya ya ? ! , atau ada alternatif laen ? Makasih
Ada EduEdi kalau di Bandung. Di sini:
Area Komersial Salman ITB counter no 5 Jl Gelap Nyawang no. 4 ( Bank Muamalat ) Pin BB 269760 Bandung
Telp. 081321136800 / 022 31002100
~~~~~~~~~~~~~~
Kalau mau beli online bisa juga di:
https://www.zenius.net/voucher-purchase-online
atau kontak langsung mobile customer service di sini:
SMS/Whatsapp: 0813 163 83978
Pin BB: 2A19FF4E
Sorry nih kayaknya ada problem dengan Disqus comment system ini jadi balesan gue kemarin kayaknya dianggap spam (mungkin karena ada link dan ada nomor telp juga).
Kita punya kok distributor di Bandung. Ada di salman ITB (di depan ITB). Namanya EduEdi. Kalau mau cari nomor kontaknya, buka zeniusmultimedia dot com terus cari list outlet resmi zenius.
Selain itu, bisa juga beli voucher langsung secara online. Buka aja zenius dot net terus klik “beli voucher”. Bisa transaksi langsung di situ, atau kontak ke mobile customer service. Ada nomornya di situ.
Oh oke sip sip thank’s bang !
zenius top deh 😀
Thanks man
bang wisnu butuh saran nih..
saya kelas 11, pengen fokus buat SBMPTN dari sekarang
buat step2nya gimana ya bang?
kebanyakan soal2 ptn materi kelas 12 soalnya
makasih bang
cicil aja mulai dari sekarang, seenggaknya di materi kelas 10 & 11 kamu mantepin dulu. Langkahnya bisa kamu lihat disini
https://www.zenius.net/blog/7-langkah-strategis-belajar-sbmptn-snmptn
thanks bang glen!
Soal PTN lebih banyak di materi kelas 12? Enggak juga sih. Malah banyak juga materi kelas 10 dan 11. Anak-anak kelas 12 yang mempersiapkan diri buat PTN juga biasanya review lagi materi kelas 10 dan 11. Nah, kalau buat lo, tipsnya gini:
(1) Kalau lagi belajar bab apapun di sekolah (misal sukubanyak), coba lo latih diri lo dengan soal-soal yang levelnya sama dengan SBMPTN. Jangan terpaku sama tipe2 soal yang keluar pas ulangan aja. Di zenius net kan ada tuh latihan soal per bab persiapan SBMPTN. Kerjain aja.
(2) Sesekali lo belajar duluan babnya sebelum guru lo ngajarin. Ini asik lagi. Cobain deh. Pas anak2 lagi pusing belajar bab itu, lo bisa main2. Hehe.
(3) Be playful. Apapun yang lo pelajarin, be playful. Make it fun. Banyak sih soal2 matematika atau fisika yang bisa bikin kita bilang “gile soalnya keren” pas tau solusinya. Terus eksplorasi juga ke berbagai ilmu lain dengan baca, browsing2. Jangan terbatas buku sekolah. Intinya sih, enjoy aja. Namanya belajar itu emang enaknya kalau kita enjoy ngejalaninnya sih. Hehe.
thanks banget bang!
kak materi2 ipsnya kapan lenkapnya sih,soalnya materi2 yang ada udah dipelajari semua !!
sorry oot. apa di sini cuma gue yang baru baru ini ngerasa load video di zenius kerasa berat?
padahal kemaren kemaren kagak. lancar jaya. gue pake tri aon.
mohon bantuannya
mau nanya nih suku banyak itu pangkatnya harus ada semua gak sih, kayak 3x^3 – 3x^2 – x + 15 atau bisa 3x^4 – 2x^2 +2x + 15. yang kedua gak ada pangkat 3 nya
Nggak kok. Nggak harus ada semua. Di contoh lo itu, kenapa pangkat tiganya nggak ada coba? Sebenernya bukannya pangkatnya nggak ada, tapi koefisien pangkat tiganya sama dengan nol. Jadi nol kali x pangkat 3 jadinya nol.
Btw, coba tonton video dari awal sampai habis deh. Udah dijelasin kok yang kayak gitu-gitu. Ini linknya untuk kelas 11 kurikulum 2013:
https://www.zenius.net/lp/cg776/bab-01-suku-banyak-polinom