Halo Sobat Zenius, apa kabar nih? Di artikel kali ini gue akan membahas materi Kelas 11 tentang rumus induksi matematika, beserta langkah-langkah pembuktiannya.
Membuktikan rumus sendiri merupakan proses belajar matematika yang tepat. Bagaimana elo bisa berlatih membuktikan rumus dengan induksi matematika? Semua akan gue share di sini.
Dalam beberapa kesempatan, baik di blog atau di video zenius.net, gue menjelaskan bahwa yang namanya belajar akan menjadi maksimal apabila elo menguasai konsepnya lebih dulu.
Nah salah satu cara melatih pemahaman konsep suatu materi dengan membuktikan rumus. Kenapa? Singkatnya gini, dengan membuktikan rumus, elo akan dituntut untuk memahami beberapa konsep sekaligus. Sebelumnya gue udah pernah nulis tentang pentingnya membuktikan rumus di sini.
Pada artikel tersebut gue udah jelasin manfaat yang elo dapet dengan membuktikan rumus, namun di situ emang belum gue jelasin secara teknis langkah-langkah induksi matematika atau cara ngebuktiin rumusnya.
Kali ini gue akan mencoba menjelaskan salah satu cara membuktikan rumus, yaitu dengan induksi matematika.

Daftar Isi
Apa sih itu induksi matematika?
Seperti yang udah gue singgung di atas, induksi matematika merupakan salah satu cara pembuktian rumus atau pernyataan matematika, atau lebih tepatnya metode pembuktian terhadap suatu pernyataan apakah pernyataan tersebut berlaku untuk setiap kasus. Supaya kebayang, sebaiknya kita langsung ke contoh kasus deh. Kasus yang seperti apa sih yang bisa diselesaikan dengan rumus induksi matematika? Kita masuk ke contoh yang sederhana aja deh ya. Misalkan gue punya deret bilangan seperti di bawah ini.
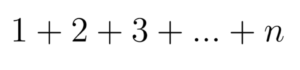
Langkah awal pembuktian untuk setiap n bilangan asli adalah nilai n tertentu, kita bisa mencari jumlah dari deret bilangan di atas. Sebagai contoh, untuk n=2, kita mendapatkan hasil demikian:
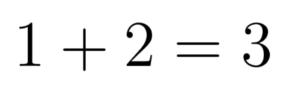
Ternyata untuk n=2, kita mendapatkan bahwa jumlah deretnya adalah 3.
Bagaimana dengan n=5? Gampang, tinggal kita hitung aja lagi begini:
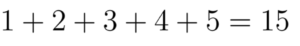
Jumlahnya adalah 15. Kalau untuk n=8 gimana? Sama aja caranya:
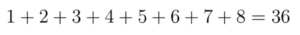
Kita dapatkan bahwa untuk n=8, jumlah deret tersebut adalah 40.
Kemudian sudah mendapatkan informasi bahwa ternyata untuk menghitung jumlah deret tersebut untuk n bilangan asli berapapun, SUDAH ADA RUMUSNYA. Jadi, nggak perlu repot-repot menjumlahkan satu per satu seperti di atas, tapi tinggal kita masukkan saja nilai n ke dalam rumus tersebut. Bagaimana tuh rumusnya? Untuk deret di atas, rumus jumlahnya adalah demikian:
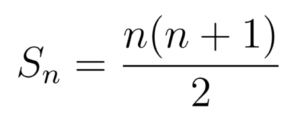
Wah, asik nih udah ada rumusnya. Berarti tinggal kita masukkin aja nilai n ke persamaan di atas untuk mencari jumlah deret tersebut. Nggak perlu jumlahin satu per satu. Nah, tapi sebagai matematikawan yang baik, kita harus skeptis nih, tahu dari mana bahwa rumus di atas itu benar? Tahu dari mana bahwa rumus tersebut berlaku untuk seluruh nilai n bilangan asli? Atau sederhananya,
Gimana Buktiinnya?
Yup. Gimana buktiinnya kalo rumus Sn di atas udah bener?
Nah, sebelum masuk ke pembuktian dengan Induksi Matematika, coba deh kita tes dulu apakah nilai Sn itu benar untuk nilai-nilai n yang sebelumnya udah kita hitung. Kita mulai dari n=2.
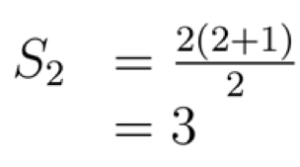
Wah, ternyata benar nih. Hasilnya sama untuk n=2. Sekarang coba kita tes untuk n=5.
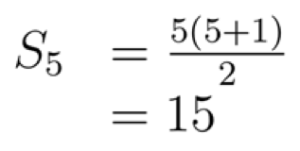
Hasilnya sama lagi nih. Untuk n=8 gimana?
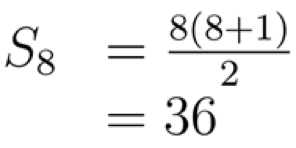
Bener lagi! Okay, kalau gitu, bisa kita simpulkan bahwa rumus Sn ini benar lah ya? Eit, tunggu dulu. Kita baru menguji untuk tiga nilai n. Dalam matematika, kita tidak bisa melakukan generalisasi seperti itu. Untuk bisa membuktikan bahwa rumus Sn ini benar untuk semua kasus, kita harus benar-benar bisa membuktikan bahwa rumus Sn ini benar untuk SEMUA nilai n bilangan asli.
Wah, kalau mau membuktikan untuk semua nilai n, kapan selesainya? Kan ada banyak banget yang harus dicoba. Nilai n=9, nilai n=10, nilai n=100, nilai n=84349384, dan seterusnya. Ada tak hingga nilai n yang harus kita coba. Nggak mungkin bisa kita cobain semuanya.
Nah, itulah sebabnya kita perlu membuktikannya dengan menggunakan Induksi Matematika.
Setelah elo baca penjabaran di atas, dapat disimpulkan bahwa ada tiga langkah dalam induksi matematika yang diperlukan untuk membuktikan sebuah rumus, yaitu:
- Membuktikan bahwa rumus atau pernyataan tersebut benar untuk n = 1.
- Mengasumsikan bahwa rumus atau pernyataan tersebut benar untuk n = k.
- Membuktikan bahwa rumus atau pernyataan tersebut benar untuk n = k + 1.
Untuk menerapkan induksi matematika, kita harus bisa menyatakan pernyataan P (k + 1) ke dalam pernyataan P(k) yang diberikan. Untuk menyatakan persamaan P (k + 1), substitusikan kuantitas k + 1 ke dalam pernyataan P(k).
Sebelum lanjut, pastiin dulu elo udah punya aplikasi Zenius ya, biar bisa dapetin akses ke ribuan video pembelajaran dan latihan soal. Kalo belum install, langsung aja download dengan klik gambar di bawah ini!
Konsep Dasar Induksi Matematika
Dengan menggunakan Induksi Matematika, kita bisa membuktikan rumus Sn di atas tanpa perlu menghitung satu per satu nilai Sn seperti di atas. Caranya simple banget. Kita cuma butuh melakukan dua langkah berikut ini:
- Buktikan bahwa rumus tersebut benar untuk nilai n dasar (pada contoh di atas, buktikan untuk n=1).
- Buktikan bahwa jika rumus tersebut benar untuk n=k, maka rumus tersebut juga benar untuk n=k+1.
Okay, sampai di sini, coba elo STOP BACA dulu untuk mikir, emangnya kenapa dua langkah tersebut bisa membuktikan Sn benar untuk SEMUA nilai n bilangan asli?

Hayo dipikir dulu…

TETOT! Waktunya abis. Jawabannya adalah, karena efek domino.
Efek Domino
Elo pasti tau atau pernah maen domino kan? Yah, bahasa gaulnya gaple :p Emangnya apa nih hubungan antara domino atau gaple ini dengan induksi matematika? Coba kita lihat kedua langkah tersebut satu per satu ya. Mulai dari langkah pertama.
LANGKAH 1: Buktikan bahwa Sn benar untuk n=1.
Langkah pertama ini gampang banget. Tinggal kita masukkan nilai n=1 ke persamaan, terus kita hitung deretnya, beres. Kesimpulannya: S1 benar (Sn benar untuk n=1). Lanjut ke langkah 2.
LANGKAH 2: Buktikan bahwa jika benar untuk n=k, maka dia benar juga untuk n=k+1.
Ini bagian menariknya. Karena pada langkah pertama kita sudah membuktikan bahwa Sn benar untuk n=1, berarti dia benar juga untuk n=2. Kalau Sn benar untuk n=2, maka Sn benar juga untuk n=3. Kalau Sn benar untuk n=3, maka Sn benar juga untuk n=4. Dan seterusnya sampai n tak hingga.
Kalau penjelasan di atas masih kurang jelas, coba telaah pelan-pelan deh ya. Jadi bayangkan bahwa pembuktian yang kita lakukan di langkah 1 dan 2 tadi kita nyatakan dalam dua premis, premis 1 untuk pernyataan pada langkah 2 dan premis 2 untuk pernyataan pada langkah 1. Jadinya begini:
Premis 1: Jika Sn benar untuk n=k, maka Sn benar untuk n=k+1
Premis 2: Sn benar untuk n=1
Kesimpulan: ?
Nah, kalau kita memiliki dua premis seperti itu, apa kesimpulan yang dapat diambil? Berhubung nilai k=1, berarti k+1 itu adalah 2 dong ya? Berarti kesimpulan dari pembuktian induksi matematika adalah Sn benar untuk n=2. Sekarang kita lanjutkan lagi dengan kesimpulan barusan kita masukkan ke dalam premis 2.
Premis 1: Jika Sn benar untuk n=k, maka Sn benar untuk n=k+1
Premis 2: Sn benar untuk n=2
Kesimpulan: ?
Kesimpulannya adalah? Gampang ya, yaitu Sn benar untuk n=3. Ini masih bisa kita lanjutkan lagi dengan teknik yang sama. Kesimpulan ini kita jadikan premis 2.
Premis 1: Jika Sn benar untuk n=k, maka Sn benar untuk n=k+1
Premis 2: Sn benar untuk n=3
Kesimpulan: ?
Apa kesimpulan dari kedua premis di atas? Yup, kesimpulannya adalah, Sn benar untuk n=4. Elo bisa lanjutkan proses ini sampai seterusnya kalau mau. Tapi pada suatu titik kita harus berhenti melakukan ini dan mulai berpikir lagi.
Jadi, kalau proses ini kita lanjutkan, kita akan mendapatkan kesimpulan bahwa Sn benar untuk semua n bilangan asli.
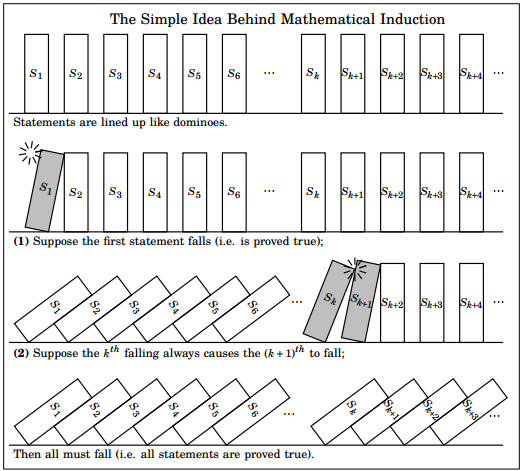
Inilah sebabnya Induksi Matematika sering juga dikait-kaitkan dengan efek domino. Seperti efek domino, meskipun kita cuma menjatuhkan domino yang pertama, akibatnya adalah seluruh domino tersebut akan jatuh secara bergantian, seperti animasi di bawah ini.

Ups, maksudnya ini

Pembuktian dengan Induksi Matematika
Nah, di atas kita udah mempelajari konsep dasar dari Induksi Matematika ya. Sekarang, kita lanjut ke proses pembuktian dengan Induksi Matematikanya. Kita balik lagi ke contoh di atas, yaitu deret ini:
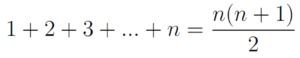
Deret ini memiliki Un = n dan Sn = n(n+1)/2. Coba kita buktikan dengan Induksi Matematika bahwa rumus Sn ini benar.
LANGKAH 1: Buktikan bahwa Sn benar untuk n=1.
Bagian ini gampang nih. Kita tahu bahwa untuk n=1, jumlahnya harus sama dengan 1. Berarti kalau S1 itu sama dengan 1, langkah satu beres.
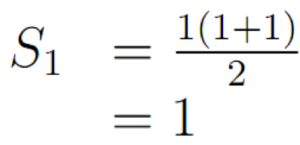
Sip. Rumus Sn ini lolos pada langkah satu. Berikutnya, langkah 2.
LANGKAH 2: Buktikan bahwa jika Sn benar untuk n=k, maka Sn juga benar untuk n=k+1.
Nah, untuk bagian ini, teknik membuktikannya adalah dengan membuktikan bahwa persamaan di bawah ini benar.
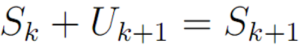
Kalau persamaan di atas benar, itu sama saja dengan membuktikan bahwa jika Sk benar, maka Sk+1 juga benar.
So, kalau kita masukkan n=k dan n=k+1 pada rumus Sn, maka kita akan mendapatkan:

Kalau begitu, tinggal kita buktikan saja dengan cara demikian:
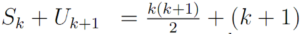
Bagian (k+1)-nya kita kotakin kemudian kita keluarkan (hukum distributif)
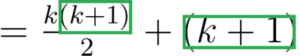
Sehingga kita dapatkan:
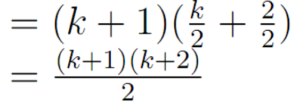
Ternyata hasilnya sama peris dengan Sk+1 yang kita hitung pada tabel di atas. Berarti kita dapat simpulkan bahwa persamaan berikut ini:
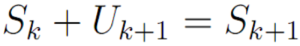
Adalah benar!
Karena Sn terbukti benar pada langkah 1 dan juga terbukti benar pada langkah 2, maka kita bisa simpulkan bahwa rumus Sn benar untuk semua n bilangan asli! Q. E. D.*
Induksi vs Deduksi
By the way, emang kenapa sih kok metode seperti ini diberi nama Induksi Matematika? Apakah ada hubungannya dengan penalaran induktif dalam logika? Nah, sebenernya nggak ada hubungannya karena penalaran yang digunakan dalam Induksi Matematika ini justru penalaran deduktif, bukan penalaran induktif. Loh, kok gitu? Nah, supaya tahu kenapa begitu, kita coba pelajari dulu apa bedanya penalaran induktif dengan penalaran deduktif
Penalaran Induktif yang Beneran
Penalaran induktif yang beneran itu tidak ada hubungannya sama sekali dengan Induksi Matematika.
Sederhananya, penalaran induktif mengambil kesimpulan dari premis-premis umum (pengamatan, data, fakta) lalu kemudian mengambil kesimpulan yang bersifat spesifik (hipotesis).
Jadi, kesimpulan yang diambil dari penalaran induktif itu sifatnya tidak pasti, melainkan “mungkin benar”. Salah satu kecenderungan umum dari penalaran induktif itu adalah dia mengambil kesimpulan general dari berbagai kasus khusus. Contohnya begini:
Joni sering bepergian keliling dunia. Ketika dia ke Amerika, dia melihat seluruh angsa di sana warnanya putih. Ketika dia pergi ke Eropa, dia melihat seluruh angsa di sana warnanya putih juga. Ketika dia pergi ke Tiongkok, ternyata seluruh angsa di sana warnanya juga putih. Akhirnya dia berkesimpulan bahwa seluruh angsa di dunia ini warnanya putih.
Pada contoh di atas, Joni melakukan generalisasi dari berbagai kasus khusus yang dia lihat. Penalaran yang dilakukan Joni ini adalah penalaran induktif. Di sini elo bisa lihat bahwa penalaran semacam itu masih mungkin salah. Bahkan pada kasus ini, ya kesimpulannya memang salah. Kalau aja Joni sempet dateng ke Australia, dia akan melihat angsa yang berwarna hitam di sana. Jadi, kesimpulan bahwa seluruh angsa di dunia ini berwarna putih itu salah.
Terus, apakah argumen induksi ini tidak bisa dijadikan argumen yang kuat? Argumen induksi ini bisa merupakan argumen yang lemah (seperti contoh angsa di atas), bisa juga merupakan argumen yang kuat. Metode ilmiah yang kita gunakan di sains itu juga menggunakan penalaran induktif kok.
Contohnya di artikel Fanny yang membahas penelitian tentang rokok. Penelitian tersebut dilakukan kepada segelintir orang, tapi kita bisa mengambil kesimpulan secara general bahwa itu berlaku pada semua orang. Apakah kesimpulannya bisa salah? Bisa. Tapi kemungkinannya kecil karena penelitian semacam itu sudah diulang berkali-kali dengan berbagai konteks dan hasilnya sama.
Penalaran Deduktif
Nah, sekarang kita masuk ke penalaran deduktif. Penalaran deduktif merupakan pengambilan kesimpulan secara logis berdasarkan premis-premis yang ada.
Dari definisi ini jelas ya bahwa penalaran deduktif itu sifatnya pasti. Dalam penalaran deduktif, tidak ada generalisasi. Contoh penalaran deduktif itu seperti ini:
Premis 1: Semua orang akan mati
Premis 2: Socrates adalah orang
Kesimpulan: Socrates akan mati
Contoh di atas adalah contoh klasik penalaran deduktif. Jadi kalau premis 1 dan premis 2 itu benar, maka kesimpulannya juga sudah pasti benar juga. Kita lihat contoh lain yah.
Premis 1: Semua bebek kakinya tiga
Premis 2: Donal adalah bebek
Kesimpulan: Donal kakinya tiga
Nah, di sini kayaknya ada yang salah nih, kok Donal kakinya tiga. Bukannya dua? Apakah kesimpulan di atas itu benar? Well, gara-gara premisnya salah, kesimpulannya jadi salah juga. Tapi penalaran di atas itu adalah penalaran yang valid secara deduktif. Kenapa valid? Karena kalau kita asumsikan premis 1 itu benar, dan premis 2 itu benar juga, maka “Donal kakinya tiga” adalah kesimpulan yang valid, atau bahasa Indonesianya, kesimpulan yang sah.
Biar lebih jelas elo bisa lihat gambar di bawah ini, penalaran induktif menghasilkan kesimpulan yang kuat atau lemah. Sedangkan penalaran deduktif menghasilkan kesimpulan valid dan ga valid.
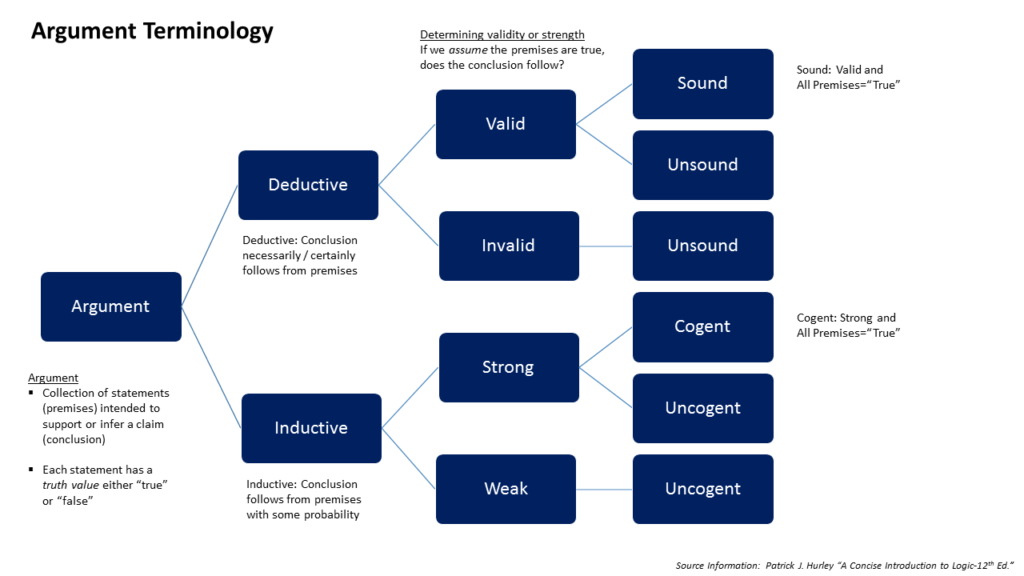
Penalaran Deduktif dalam Matematika
Penalaran deduktif ini adalah central-nya matematika. Berbagai operasi yang elo lakukan di matematika itu dasarnya adalah penalaran deduktif ini. Salah satu contoh yang paling sederhana itu gini:
Premis 1: y = 2x + 3
Premis 2: x = 2
Kesimpulan: y = 2(2) + 3 = 7
Kebayang kan? Jadi kalau kita berasumsi bahwa premis yang pertama benar (y=2x+3) dan premis yang kedua juga benar (x=2), maka kesimpulan bahwa y=7 juga merupakan kesimpulan yang valid.
Kalau kita mempelajari matematika dengan baik, sebenarnya elo bisa lihat bahwa berbagai pembuktian yang dilakukan dalam matematika itu menggunakan penalaran deduktif ini. Contohnya, ketika kita ingin membuktikan persamaan berikut ini:
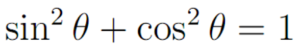
Kita tinggal gambar diagram seperti ini
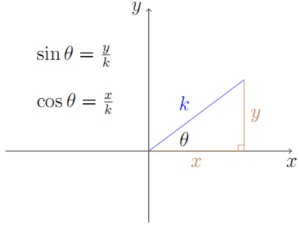
Kita mulai dengan persamaan Pythagoras pada segitiga di atas.
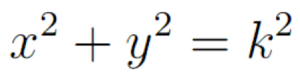
Bagi kedua ruas dengan k2.
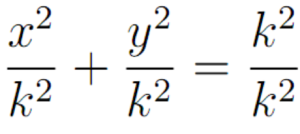
Akhirnya kita dapatkan begini:
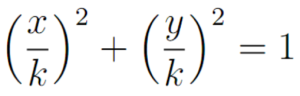
Subsitusi nilai x/k dengan cos dan nilai y/k dengan sin, maka kita dapatkan sin2?+ cos2? = 1.
Q.E.D.
Penalaran di atas menggunakan penalaran deduktif. Setiap langkahnya harus valid sehingga kesimpulan yang diambil ya sifatnya pasti, bukan mungkin.
Kalau elo mau makin ngerti lagi tentang penalaran deduktif yang kita gunakan dalam matematika, gue menyarankan elo baca juga artikel gue tentang Euclid deh. Di situ gue menunjukkan bagaimana suatu pernyataan di matematika itu bisa dibuktikan sampai ke “ujung”, di mana dia tidak bisa dibuktikan lagi. Namanya Aksioma atau Postulat.
Induksi Matematika – Deduktif atau Induktif?
Sekarang kita kembali lagi ke Induksi Matematika. Jadi sebenarnya Induksi Matematika ini menggunakan penalaran induktif atau deduktif? Dari deskripsi di atas, jelas lah ya bahwa Induksi Matematika itu menggunakan penalaran deduktif. Karena seperti yang sudah disebutkan di atas, penalaran deduktif ini sifatnya pasti. Dia tidak menggunakan generalisasi dalam mengambil kesimpulan.
Ketika kita menyimpulkan bahwa rumus Sn itu berlaku untuk semua n bilangan asli, kesimpulan itu diambil bukan dengan mengambil sample beberapa nilai n. Kesimpulan itu diambil benar-benar dengan melakukan uji secara deduktif kepada seluruh nilai n yang berada dalam ruang lingkup rumus Sn tersebut.
Gimana Sobat Zenius, sudah bisakan membuktikan pernyataan menggunakan induksi Matematika. Sulit sih kalau elo berharap dapat membuktikan hal ini dengan kalkulator induksi matematika, sebab ini semua dapat dibuktikan dengan rumus aja.
By the way, supaya nggak ada salah kaprah, Induksi Matematika itu tidak hanya dipakai untuk menjumlahkan deret suatu bilangan ya, dia bisa juga dipakai untuk membuktikan pernyataan matematika lainnya, yang biasanya melibatkan bilangan asli. Kalau elo masih belum mengerti dengan penjelasan di atas, elo bisa juga lihat penjelasan versi videonya di sini:
Berani sekalian ngetes Fundamental Skill elo? Nih, cobain Zencore! Dengan fitur adaptive learning, elo bisa tau seberapa jago kemampuan fundamental lewat kuis CorePractice, sekaligus upgrade diri biar makin cerdas. Elo juga bisa ajak temen-temen buat push rank. Klik banner di bawah buat cobain!

*) Q.E.D. itu singkatan dari Quod Erat Demonstrandum. Bahasa latin yang jika diterjemahkan secara bebas, kira-kira artinya sama dengan, “Telah dibuktikan kebenarannya”.
Sobat Zenius, ZenCore akan lebih optimal kalau elo maininnya lewat hape. Jadi pastiin elo udah download Zenius Apps ya. Biar makin mantap, Zenius punya beberapa paket belajar yang bisa lo pilih sesuai kebutuhan lo. Di sini lo nggak cuman mereview materi aja, tetapi juga ada latihan soal untuk mengukur pemahaman lo. Yuk langsung aja klik banner di bawah ini!
Originally Published: November 5, 2016
Updated By: Arieni Mayesha














Mau nanya dong ka wisnu cara nentuin Sn dari 1^2 +2^2 +3^2 +…+n^2 sama Sn dari 1^3 +2^3 +3^3 +…+ n^3 gimana ya cepetnya?
Salah satu tekniknya bisa dilihat di sini. Tapi ini udah di luar topik Induksi Matematika ya, bahkan nggak masuk pelajaran SMA. Untuk mencari rumus jumlah deret, yang dipelajari di SMA itu hanya untuk deret Aritmetika dan Geometri aja. Dua contoh deret di atas bukan merupakan deret Aritmetika maupun Geometri.
Pada materi Induksi Matematika, kita tidak diminta untuk mencari nilai Sn. Justru Sn-nya itu sudah diketahui terlebih dahulu, kemudian kita buktikan dengan Induksi Matematika. Sebagai contoh, untuk deret yang pertama, rumusnya adalah (1/6)n(n+1)(2n+1). Nah, coba gimana kita membuktikan bahwa rumus Sn tersebut benar untuk semua nilai n bilangan asli. Bisa?
kak ada referensi tentang tata cara bikin essay yang keren tap baku ga ? contohnya essay tentang diri sendiri.
Bantu jawab ya. Penurunan kedua rumus tersebut bisa dilihat di video ini: https://www.zenius.net/lp/c66… (video nomor 01 sampai 10). Sangat disarankan untuk menonton videonya secara berurutan supaya lu tidak bingung dengan penjelasan di video nomor 09 dan 10.
Min, kira2 butuh waktu berapa bulan ya untuk belajar saintek?
Tergantung. Saat ini lo udah menguasai materi seberapa banyak? Jurusan dan Universitas yang lo incer itu tingkat persaingannya gimana? Kira-kira butuh score berapa untuk bisa diterima? Jadi parameternya banyak. Ada beberapa artikel di blog ini yang pernah membahas tentang persiapan SBMPTN, salah satu contohnya di sini:
Kalo baru belajar SBMPTN sekarang, sempet ga ya?
Artikel-artikel lain tentang SBMPTN bisa dilihat di sini:
SBMPTN (zenius blog)
Wisnu, apakah pembuktian secara induksi matematika berlaku untuk nyari rumus Sn aja?
Udah dijawab bg Wisnu di atas “By the way, supaya nggak ada salah kaprah, Induksi Matematika itu tidak hanya dipakai untuk menjumlahkan deret suatu bilangan ya, dia bisa juga dipakai untuk membuktikan pernyataan matematika lainnya, yang biasanya melibatkan bilangan asli.”
Iya bener. Thanks yah Faridatul Hidayah. 🙂
Haha yoi bang..
Yup. Seperti yang udah disebutin oleh Faridatul Hidayah, induksi matematika tidak hanya dipakai untuk mencari rumus Sn aja. Contoh lainnya adalah seperti contoh soal di bawah ini.
Bisa buktiinnya? 🙂 (jawabannya ada di video nomor 9)
Gambar yang di atas nggak keluar ternyata. Maksudnya ini:
https://uploads.disquscdn.com/images/7ce09a8a9be8dc044b3199b791333c65a0985fd2d7066a87f73a2bc481bb501c.jpg
Utk n=7
7!>3^7
5040>2187 benar
Anggap n=k bener
k!>3^k…(h)
Akan dibuktikan n=k+1
(k+1)!
=(k+1)k!>3^k . 3
Karena (h) bener dan untuk (k>6) pasti (k+1)>3 maka pertidaksamaan tersebut terbukti bener untuk semua bilangan asli > 6
CMIIW
Gw ngerasa ada yg salah prosedur, cuma disebelah mana ya..?
Kurang tau etika untuk n=k+1 nya
Udah bener kok. Cuma nulisnya kurang rapih aja jadi argumennya kurang jelas.
Langkah pertama udah tepat. Langkah ke dua yang awal-awal juga udah tepat, cuma penjabaran (k+1)!nya kurang.
(k+1)! itu kita ubah bentuknya menjadi begini:
(k+1)! = (k+1)k!
Dengan asumsi bahwa k!>3^k, berarti kalau kita kalikan kedua ruas dengan (k+1), kita akan mendapatkan:
(k+1)k!>3^k(k+1)
Karena ruang lingkup pembuktiannya adalah untuk k>6, maka pasti (k+1)>3, sehingga kita mendapatkan 3^k.(k+1)>3^k.3 (kedua ruas dikalikan dengan 3^k)
Berarti:
(k+1)k! > 3^k(k+1) > 3^k.3
Nah, kalau gitu
(k+1)k! > 3^k.3
Atau
(k+1)! > 3^(k+1)
Berarti langkah ke dua terbukti.
Ooh…sip. Kurang bisa ngebahasainnya untuk n=k+1
Thanks Bang
keren artikelnya kak @wisnuops:disqus . Namun saya belum jelas kak, bedanya pembuktian rumus dengan menurunkan rumus apa ya kak? Terimakasih kak.
A)Pembuktian=kita udah dikasih deluan rumusnya.
Contoh :
Buktiin 1+3+5+7+…+(2n-1)=n²!
Jwb :
utk n=1 1=1²…benar
utk n=k+1
k²+(2(k+1)-1)
=k²+(2k+2-1)
=k²+2k-1
=(k+1)²
Jadi, karena jika u/ n=k maka n=k+1 bener, rumus tersebut berlaku untuk semua himpunan bilangan asli.
B)Menurunkan=kita nyari rumus yg lebih kompleks dari rumus sederhana.
Contoh :
Rumus asal :
Cos(a+b)=cosacosb-sinasinb..(1)
Ganti b = a
cos(a+a)=cos²a-sin²a..(2)
Ganti cos²a=1-sin²a
cos2a=1-2sin²a…(5)
Ganti sin²a=1-cos²a
cos2a=2cos²a-1..(4)
Dan bisa terus dilanjutin/diturunin sampe dapat puluhan rumus lainnya….
Hampir sama sih. Paling bedanya kalau pembuktian rumus, berarti rumus akhirnya sudah diketahui. Kita tinggal melakukan pembuktian apakah rumus tersebut benar atau tidak. Sementara kalau penurunan rumus, rumus akhirnya bisa sudah diketahui, bisa belum. Kita mencari rumus tersebut dengan menurunkannya dari hal yang sudah diketahui sebelumnya.
Di artikel di atas, ketika kita membuktikan bahwa 1+2+3+…+n = n(n+1)/2, kita sudah tahu bahwa jumlah deretnya adalah n(n+1)/2. Kita tidak perlu menurunkannya lagi. Jadi induksi matematika ini hanya dipakai untuk membuktikan rumus tersebut, bukan menurunkannya. Untuk bisa mendapatkan rumus n(n+1)/2, kita harus menurunkannya dengan menggunakan metode lain. Lo udah belajar deret artimetika belum? Kalau belum, bisa pelajari di sini: Barisan dan Deret.
Bang Wisnu, berarti kalo penalaran deduktif itu sifatnya kaku? Jadi ya kita terima aja dan itu pasti.
Kaku itu bukan istilah yang tepat sih sebenernya. Tapi kalau dibilang pasti, iya pasti. Makanya matematika sering juga disebut sebagai ilmu pasti. Selain matematika, seperti Fisika misalnya, nggak bisa disebut sebagai ilmu pasti.
Fisika knp ga dibilang ilmu pasti, bang? Padahal kan dlm fisika itu saintifik juga?
Karena kesimpulan yang diambil itu tetap melibatkan penalaran induktif yang nggak mungkin 100% pasti.
Hmm… mungkin ilustrasinya gini.
Dulu, Newton menemukan hukum Gravitasi setelah melihat persamaan matematis dari berbagai gerakan planet. Hukum Gravitasi ini dianggap berlaku secara umum untuk semua planet. Tapi ternyata, beberapa tahun setelah Newton, scientist menyadari bahwa perhitungan gravitasi newton meleset jauh untuk orbit planet Merkurius. (ini mirip dengan cerita Joni yang ketemu angsa putih di Australia). Akhirnya diperlukan hukum yang lebih general yang bisa menjelaskan orbit planet Merkurius dan planet-planet lainnya. Datanglah Einstein. Dengan Relativitas Umumnya, dia bisa menjelaskan hal itu.
Jadi, Fisika itu nggak pernah pasti. Masih mungkin pengetahuan yang kita punya sekarang itu salah (seperti kasus gravitasi newton). Sementara matematika nggak gitu. Dari dulu sampai sekarang, 1+1 ya selalu 2, dan akan begitu seterusnya.
Oooh, begitu ya bang. Berarti kalo fisika, kimia, dll, msh bisa berkembang krn ilmunya itu didasari penemuan&penelitian dan bisa berkembang terus dan diperbarui kalo misalnya ada penelitian yg lebih akurat. Mantep.
Jujur aja, ane udh pake zenius sbnernya dari kelas 3 SMA (sekarang alumni, soalnya SMA ane ngewajibin 4 taon buat semua siswanya) dan waktu itu ane pake zenius cuma buat materi aja buat UN tanpa nonton zenius learning sama baca zenius blog. Wah, kalo tau isinya blog keren keren begini mah, udh sejak kapan tau nagih jadi belajar nya, krn jadi bikin kita juga “ngeh” sama apa yg kita pelajarin. Hehe.
Mantep deh. Sukses bang.
Nah, mantab juga kesimpulannya.
Thanks yah udah pake zenius. 😀
Woke bang. Mantap.
Sdikit oot nih bang, bang Wisnu pernah nyinggung di salah satu komenan masalah kesiapan SBMPTN kita buat nentuin tujuan PTN dan jurusan yg kita pengen. Nah, kalo misalnya tingkat persaingan di jurusan itu tinggi, kiat2 nya apa aja sih, bang? Minta sarannya juga.
Pertanyaan itu kayaknya udah dijawab di artikel Glenn yang ini:
7 Langkah Strategis Belajar SBMPTN
wah, gue baru banget kemarin jumat ulangan materi ini bang. BTW buat nentuin notasi sigma dari suatu barisan atau deret gimana bang ?
Di playlist ini dibahas juga kok tentang notasi sigma:
https://www.zenius.net/lp/c4572/induksi-matematika-teori
Video terakhir
Sorry nih bang agak nyimpang dari artikel. Apa sih yang ngebuat bang Wisnu jatuh cinta sama matematika? ? (pecinta matematika yang lain jg diharapkan untuk menjawab)
Ini agak panjang ceritnya. Mulai dari bermain-main sama teka-teki matemtika, ngobrolin matematika dll sama orang-orang yang juga suka, ketemu guru yang asik, ketemu buku yang seru, dsb.
Kalau disimpulin, mungkin faktor-faktor ini kali yang berpengaruhnya paling besar:
– Gue melakukan eksplorasi terhadap matematika itu atas keinginan sendiri, bukan paksaan dari orang lain.
– Hal kecil seperti menemukan solusi dari persoalan matematika bikin nagih pengen ngerjain lagi. Akhirnya jadi makin sering bermain-main dengan matematika, tanpa sadar gue melakukan deliberate practice di matematika selama bertahun-tahun. Ketika skill gue naik, kesukaan gue terhadap matematika juga naik.
Jujur nih bang gue tu gak suka sm matematika, jadi tiap belajar mtk tu tekanan batin bgt. Buat gue jatuh cinta sama mtk dong bang..
Belajar matematika biasanya mengikuti bab di sekolah atau di luar yang lagi dipelajari di sekolah?
Kalau mengikuti bab di sekolah memang gue sendiri kadang suka ngerasa matematika itu jadi nggak menarik sih, karena berasa kepaksa itu. Tapi ketika gue belajar mandiri, ngatur jadwal sendiri mau belajar apa, dsb… itu jauh lebih enak.
Kalau bingung mau mulai dari mana untuk eksplorasi ilmu, bisa dimulai dengan baca-baca artikel blog kita sih. Banyak orang yang bilang setelah baca artikel-artikel kita jadi suka matematika. Mungkin lo tertarik untuk nyoba. Misalnya mulai dari artikel Bisa nggak sih 2+2=10? atau Euclid (dan konsep postulat).
Haha ya bang gue udah baca yang 2+2=10 dan emg nyenengin..Duh makasih banyak bang… tapi terus yang materi di sekolahnya disampingin gitu bang?
Mantab. Materi sekolahnya menurut gue boleh lo kesampingkan dulu kalau lo masih merasakan tekanan batin ketika belajar, karena kalau dipaksakan ya percuma. Eksplorasi aja dulu ke mana-mana sampai lo merasa bahwa matematika itu sebenarnya menyenangkan. Nanti ketika udah “sembuh” (dari tekanan batin yang lo sebutin itu), balik lagi ke pelajaran sekolah gue rasa lebih enak rasanya.
Siap! bakal gue coba. Thanks ya bang.. ?
Gue suka dengan matematika karena matematika itu masuk-akal dan saling berhubungan satu sama lain. Masuk akal dalam arti ada penjelasan yang logis mengapa suatu hal bisa terjadi. Contohnya, dengan memahami definisi dari gradien garis lurus: m=(y2-y1)/(x2-x1), x1/=x2, kita bisa menjelaskan mengapa persamaan garis y=mx+k adalah benar. Sedangkan saling berhubungan artinya setiap topik-topik di matematika itu terkait erat satu sama lain. Contohnya, topik logaritma berkaitan erat dengan topik eksponen karena logaritma merupakan kebalikan dari eksponen, topik integral berkaitan erat dengan topik turunan dan limit, dsb.
Pernah ketemu sama orang yang benci matematika gak? Gimana nanggepinnya?
Pernah saja. Gue cuma menyarankan mereka untuk mengubah cara belajar mereka di matematika dengan cara tidak menghafal apa yang sedang dipelajari. Itu saja.
Gue gak ngehafal tp ttp ogah bang..
Oke deh bang makasih ya sharingnya… ?
Bang gue mau nanya nih, bisa ngga sih kita deduksi kayak Sherlock Holmes, terutama kayak di TV serialnya BBC UK “Sherlock” itu. Sebenernya science of deduction-nya Sherlock pasti beneran ada kan bang?
Hehe. Gue nggak pernah nonton serialnya, tapi pernah baca bukunya. Menarik sih. Tapi kata deduksi di buku itu sering dipakai keluar dari konteksnya. Penalaran yang dipakai oleh Holmes dalam “science of deduction”-nya itu sebenernya juga penalaran Induktif. Ada penjelasannya di Quora dan di Medium. Jadi science of deduction-nya Sherlock Holmes dalam kehidupan nyata ya bagaikan science aja, which is masih menggunakan penalaran induksi, bukan deduksi. Sorry kalau mengecewakan. 🙂
Oh gitu ya. Gue emang kadang kalo nonton juga mikirnya tuh “emang udah
pasti begitu kesimpulannya?” pantesan, ternyata itu penalaran induksi
ya. Makasih banyak bang Wisnu.
bang OOT nih, smoga lo baca komen ini, gua cuma mau minta tanggapan elo atau siapapun yg baca nih komen, “Kita mau masuk jurusan yang kita idam2kan, yg menjadi masalah adalah syarat untuk tidak buta warna(parsial/total)” nah ngatasin hal ini gmn ya? apakah lanjut atau gmn :”((
Kalau memang syaratnya tidak buta warna, sebaiknya jangan dipilih sih jurusan tersebut. Rencananya mau masuk jurusan apa?
arsitektur bang:”( Ohh god
Kalo masuk SAPPK ITB kayaknya sih kaga. Coba liat di http://usm.itb.ac.id/wp/?page_id=38 disitu ga dicantumin SAPPK. (CMIIW)
Semoga membantu.
Sorry OOT, sebenernya udah lama mau nanya tp nunggu ada artikel baru. Jadi gua adalah salah satu siswa yang pengen ambil jurusan SOSHUM untuk SBMPTN, sedangkan gua IPA. Nah sementara itu masih ada UN kan, ada ga cara untuk nyeimbangin antara belajar SBMPTN yg materinya IPS dan UN yg materinya IPA? Apa harus ada yg gua korbanin?
Kalau itu, kira pernah bahas di artikel yang ini:
Tips belajar SBMPTN untuk lintas jurusan
Berarti pembuktiin seperti ini gaberlaku buat fisika ya bang?cuma buat matematik karna sifatnya pasti/deduktif?
Yup. Induksi matematika hanya untuk membuktikan pernyataan matematika. Nggak berlaku untuk membuktikan pernyataan ilmu lainnya, termasuk fisika.
Meskipun begitu, jangan lupa bahwa fisika juga menggunakan matematika. Sebagai contoh, perhatikan pernyataan di bawah ini:
Semua benda yang dijatuhkan di atas permukaan bumi, akan mengalami percepatan gravitasi sebesar g = 9,8m/s2.
Pernyataan di atas adalah pernyataan fisika. Bagaimana cara kita bisa mengambil kesimpulan dari pernyataan tersebut? Tentu dengan melakukan eksperimen. Misalnya kita melakukan eksperimen ini di Jakarta, Surabaya, Malang, Denpasar, dan Gorontalo dan mendapatkan bahwa pernyataan tersebut benar. Kemudian kita generalisasi bahwa ini berlaku di seluruh bumi. Ini adalah bagian penalaran induktifnya.
Sekarang, ketika kita sudah cukup yakin bahwa pernyataan tersebut benar. Berbagai konsekuensi dari pernyataan tersebut bisa kita deduksikan secara matematis. Contoh:
Kalau gue melepaskan batu pada t=0, maka pada t=1, berapa kecepatannya? Well, karena percepatannya adalah 9,8m/s2, berarti dalam satu detik, kecepatannya menjadi 9,8m/s.
Pada t=2, berapa kecepatannya? Karena percepatannya adalah 9,8m/s2, berarti setelah dua detik, kecepatannya menjadi 19,6m/s.
Pada t=3, berapa kecepatannya? Karena percepatannya adalah 9,8m/s2, berarti setelah tiga detik, kecepatannya menjadi 29,4m/s.
Kita bisa yakin bahwa ketiga kesimpulan di atas valid, dan pasti benar kalau premisnya benar (kalau g = 9,8m/s2).
sorry OOT bang wisnu, bang kawan2 gua ga di sekolah ga di kuliah hampir semua menyontek pas ujian/kuis, gua bete banget berasa ga adil. gimana caranya menghadapi yang begituan bang? thanks
Kak, beasiswa prestasi untuk melanjutkan s1 di ptn selain bidikmisi apa saja ya? Mohon infonya. Saya pernah juara osn astronomi dan kimiaa tingkat kabupaten.
kak wisnu ? ada ga referensi tentang tata cara bikin essay yang keren, tapi juga baku sesui dengan struktur + kaidahnya ?
OOT ya kak. kak wisnu ? ada referensi tentang tata cara bikin essay yang keren, tapi juga baku gak ? essay ttg diri sendiri isinya.
kak wisnu ?
kak sabda,mnta tips sma rencana bljarnya dong, buat first-time nih, yg mau perang buat sbmptn 2017,btw ane telat kagak ya baru bljr sekarang,
Bang wisnu kalo mau belajar saintek dari awal lg, kira2 butuh berapa bulan ya bang?
bang kasih tips biar motivasi belajar gak naik turun. gw kalo belajar kadang bisa sampe berjam-jam, tapi kadang juga gak belajar sama sekaliiiiiiiiiiiiiiii :((((
kaak materi SBM yg geografi blm lengkap ya kayaknya? bagian pedosfernya gaada, pdhl gue lg galau2nya sm itu materi;(
Bang wisnu,sory nih gw keluar dari topik,kita zenius club 16/17 butuh banget tentor dari zenius. Bang wisnu mau kgk join ke grup line kita??
lah, trus kenapa dinamai “induksi matematika” bang? padahal matematika itu bersifat deduktif, pasti. kenapa namanya bukan “deduksi matematika” aja? kan buat bingung yee
Kak wisnu mau tanya.. kenapa pada induksi matematika hanya terbatas pada bilangan asli saja??? Kenapa tidak bilangan bulat kak???
Hmm… seperti yang sudah dijelaskan di atas, pembuktian pada induksi matematika itu lompat-lompat dan biasanya selisihnya 1, seperti selisih antara bil asli yang satu dengan yang lainnya.
n=1, n=2, n=3, dst.
Sebenernya bisa nggak sih kalau kita menggunakan induksi matematika tapi dengan selisih nggak satu, misalnya selisihnya 1/2. Bisa-bisa aja.
Pada langkah pertama, buktikan bahwa persamaan tersebut berlaku untuk n=1/2 misalnya. Kemudian pada langkah berikutnya, buktikan bahwa jika n benar, maka n+1/2 juga benar. Dari dua langkah itu, kita membuktikan bahwa ini benar untuk:
n=1/2, n=1, n=1 1/2, n= 2, dst.
Nah, tapi biar bagaimanapun, selalu ada jarak antara suku satu dengan suku lainnya. Pada kasus ini, kita belum membuktikan untuk n=3/4 misalnya.
Jadi sebenernya bukannya induksi matematika tidak bisa digunakan untuk membuktikan yang bilangan bulat. Tapi dia tidak bisa digunakan untuk membuktikan sesuatu yang sifatnya kontinu. Sementara kalau kita mau membuktikan untuk SELURUH bilangan bulat, pasti kita harus pakai teknik pembuktian-pembuktian yang kontinu.
berguna dan bermanfaat..
Hallo saya mau nanya. Apakah induksi matematika cuma persamaain Itu sajakah atau ada persamaan lain untuk mencari rumus sn dan apakah Itu bisa untuk semua soal induksi matematika yang sejenis ?
Pertanyaan bagus nih. Induksi matematika itu nggak hanya untuk membuktikan rumus Sn. Tapi bisa juga untuk membuktikan persamaan (atau pertidaksamaan) yang menggunakan bilangan asli. Contohnya pertidaksamaan di bawah ini. Kebayang nggak gimana caranya membuktikan bahwa itu adalah pertidaksamaan yang valid dengan menggunakan induksi matematika?
https://www.zenius.net/assets/q-img/fa93048eafb8f5ca0783f29598e9c25246eeef46.jpg
Video pembuktian ekspresi matematika dengan induksi matematika gaada ya bang?
maaf, video nya itu gak bisa didownload?
Ka Wisnu, kakak tau gak caranya dapetin rumus n(n+1)/2 dari pola 1+2+3+4+…+n?
Bantu jawab ya. Penurunan rumus tersebut bisa dilihat di video ini: https://www.zenius.net/lp/c6646/notasi-sigma-teori (video nomor 01 sampai 08). Sangat disarankan untuk menonton videonya secara berurutan supaya lu tidak bingung dengan penjelasan di video nomor 08.
Gue ips tapi diajarin
Terlihatnya mudah, tapi kok susah yah…semangat semangat…
Bang wisnu, saya sebenarnya mengerti maksudnya tetapi susah untuk memahami ini ya..
saya bingung K’nya itu apa? apakah k nya adalah variable yang bernilai n?
Misalnya n = 1. maka n = k, berarti k = 1?
Bisa peke deduksi dari notasi sigma k menuju n untuk nilai k berpangkat. Jadi selanjutnya bisa kita jabarin kalo misal k^3, maka itu setara dengan nilai (k-1)^3 dikurangi -3k^2+3k-1 kan udah deh tinggal dipindah pindah ruas persamaannya ntar balik ke basic nya yaitu bilangan artimatika. Dari situ ketemu ntar rumus cepet nya di jawaban akhir