Artikel ini membahas tentang Tabung, rumus volume tabung, dan penerapannya pada contoh soal.
Sobat Zenius, lo tahu pipa, gak? Pernah melihat pipa sebelumnya? Lo tahu gak, bentuk pipa itu memiliki nama tersendiri loh! Yak, namanya adalah tabung!
Pada artikel ini, gue bakal ngebahas lebih jauh mengenai tabung, khususnya mengenai rumus volume tabung dan cara penggunaannya. Sebelum kita bahas lebih jauh, kira-kira tabung itu apa, ya?
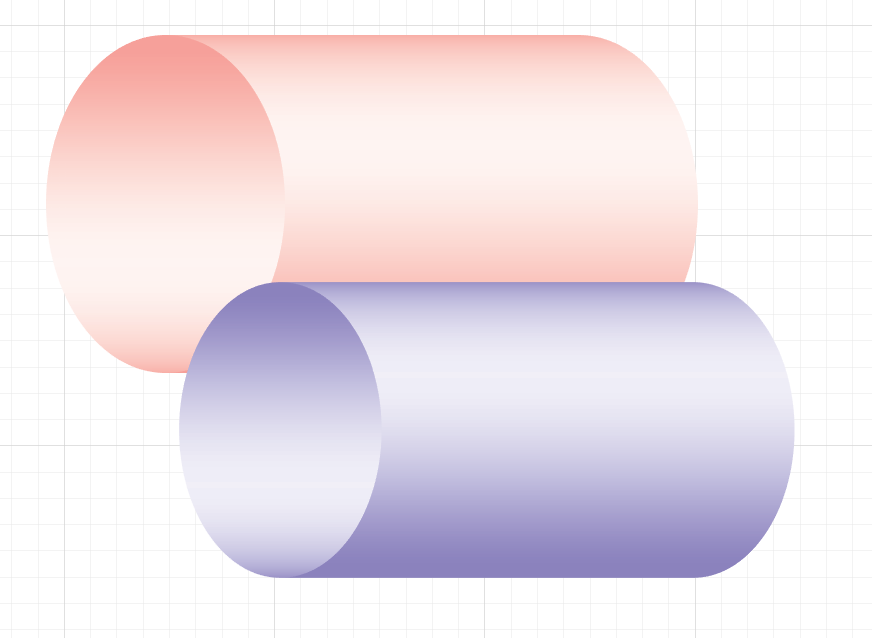
Tabung atau juga dikenal sebagai silinder adalah salah satu bentuk bangun ruang 3 dimensi dasar. Bangun ruang 3 dimensi berarti suatu bentuk yang memiliki 3 komponen utama, yakni sisi, rusuk, dan titik sudut. Sisi adalah area yang terbentuk karena rusuk, rusuk adalah garis-garis yang membentuk sisi, sementara titik sudut adalah titik pertemuan antar rusuk.
Apa itu Tabung?
Tabung sendiri adalah bangun ruang 3 dimensi yang dibentuk oleh 2 buah lingkaran yang identik dan sejajar serta persegi panjang yang mengelilingi kedua lingkaran tersebut. Kedua lingkaran disebut ‘alas’ dan ‘tutup’ tabung, sementara persegi panjang yang menghubungkan keduanya disebut ‘selimut’ tabung. Dari penjelasan di atas, bisa lo simpulkan bahwa tabung memiliki 3 sisi dan 2 rusuk.
Bentuk tabung seperti gambar di bawah ini!

Rumus Volume Tabung
Nah, gue secara spesifik akan menjelaskan soal rumus volume tabung, artinya rumus yang bisa lo gunakan untuk menghitung dan menentukan volume dari sebuah tabung. Volume itu apa, sih? Volume adalah kuantitas atau jumlah kapasitas dari suatu 3 dimensi yang terdiri dari permukaan tertutup. Maksud kapasitas di sini adalah jumlah benda (misalnya, benda cair atau gas) yang bisa ditampung oleh ruang dari bentuk 3 dimensi tersebut.
Rumus volume tabung adalah:
V = volume tabung
π = konstanta yang bernilai atau 3,14
r2 = jari-jari lingkaran pada tutup dan alas tabung, jari-jari merupakan setengah dari diameter lingkaran
d = diameter lingkaran pada tutup dan alas tabung, bila diketahui diameter maka setengah dari diameter adalah jari-jari
t = tinggi atau nilai rusuk persegi pada tabung
Nah, biar ga bingung, gue bakal kasih contoh penerapan rumus volume tabung. Misal, diketahui terdapat suatu tabung dengan jari-jari 7cm dan tinggi 10 cm. Maka, cara untuk menghitung volume dari tabung tersebut adalah:
V = π . r2 . t
V = π . r . r . t
= 22/7 x 7 x 7 x 10
= 22/7 x 49 x 10
V = 1540 cm3
Gimana, mudah bukan? Biar lebih jago, kita coba latihan dengan beberapa soal cerita di bawah, ya!
- Misalnya, terdapat suatu kaleng timah dengan diameter 6 cm dan tinggi 5 cm. Bu Mirna ingin mengisi kaleng timah tersebut dengan sambal. Berapa kapasitas sambal yang bisa ditampung oleh timah dalam mL (mililiter) ?
Diketahui
D = 6 cm
t = 5 cm
r = 6/2 = 3 cm
Jawaban
V = π . r . r . t
= 3,14 x 3 x 3 x 5
= 141,3 cm3 = 141,3 mL
Maka, sambal yang bisa ditampung oleh satu kaleng timah milik Bu Mirna adalah sebanyak 141,3 mL
- Terdapat sumur dengan jari-jari 5 m dan tinggi 12 m yang masih kosong. Bila Pak Wawan ingin mengisi sumur tersebut dengan air, berapa Liter air yang diperlukan hingga sumur terisi penuh?
Diketahui
r = 5 m = 500 cm
t = 12 m = 1200 cm
Jawaban
V = π . r . r . t
= 3,14 x 500 x 500 x 1200 cm
= 942.000.000 cm3 = 942.000 Liter
Maka, jumlah air yang diperlukan Pak Wawan untuk mengisi sumur tersebut hingga penuh adalah sebanyak 942.000 Liter
- Terdapat kaleng gas oksigen berbentuk tabung dengan diameter 20 cm dan tinggi 50 cm. Berapa kapasitas gas yang dapat mengisi kaleng tersebut dengan penuh dalam cm kubik?
Diketahui
D = 20 cm
t = 50 cm
r = 20/2 = 10 cm
Jawaban
V = π . r . r . t
= 3,14 x 10 x 10 x 50 cm
= 15.700 cm3
Maka, kapasitas kaleng oksigen tersebut adalah 15.700 cm3
Nah, itu dia penjelasan dan contoh soal mengenai volume tabung, Sobat Zenius! Lo bisa pelajari lebih jauh dengan menonton video Zenius di bawah ini, ya
https://www.zenius.net/lp/cg168/bab-04-luas-dan-volume-kelas-6-sd
Lo juga bisa baca soal rumus-rumus tabung lainnya pada artikel ini. Selamat belajar!








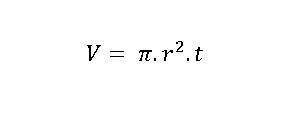
Leave a Comment