Hubungan Antar Himpunan dan Contoh Soalnya

Hai, Sobat Zenius! Elo masih inget nggak materi tentang himpunan? 

Kalau masih inget, coba deh tebak, dari beberapa kumpulan himpunan berikut, mana nih yang merupakan himpunan yang tepat?

1. Himpunan hewan berkaki empat
2. Himpunan wanita cantik
3. Himpunan bilangan ganjil 

Yang mana nih menurut elo yang merupakan sebuah himpunan?

Yup, bener banget, yang merupakan himpunan adalah himpunan nomor satu dan nomor tiga. Kenapa gitu sih? Yuk, kita bahas lebih lanjut!

Pengertian Himpunan

Seperti yang mungkin elo udah tahu, himpunan adalah kumpulan dari objek tertentu yang memiliki definisi yang jelas dan dianggap sebagai satu kesatuan. 

Pada himpunan nomor satu dan tiga, definisi yang dimiliki jelas, kayak hewan berkaki empat pasti semua tahu dong yang mana aja, begitu juga dengan bilangan prima. Tapi, kalau himpunan wanita cantik, tentu setiap orang punya punya pendapatnya masing-masing kan? Sehingga definisi yang dimiliki nggak jelas. 

Baca Juga: 3 Cara Menyatakan Himpunan Matematika

Nah, kalau elo udah inget nih himpunan itu kayak apa, kali ini gue akan ngajak elo buat ngebahas tentang hubungan antar himpunan. Kayak apa sih hubungan antar himpunan itu? Contohnya gimana ya? 

Yuk, biar nggak makin penasaran, simak penjelasan gue berikut ya!

Baca Juga: Materi dan Contoh Soal Pengetahuan Kuantitatif

.

Hubungan Antar Himpunan

Sekarang, gue akan ngajak elo buat memahami empat hubungan antar himpunan yang ada. 

1. Himpunan Saling Lepas atau Saling Asing

Apa sih himpunan saling lepas atau disebut juga dengan saling asing itu?

Himpunan saling lepas atau saling asing merupakan dua himpunan yang tidak memiliki anggota persekutuan yang sama. 

Hah? Gimana tuh maksudnya? Oke, biar elo ada bayangan gue akan kasih contohnya ya, coba elo perhatikan.

Contoh:

A = {1, 2, 3, 5} dan B = {4, 6, 7}

Coba deh elo liat kedua himpunan A dan B di atas. Apakah elo melihat ada anggota himpunan A yang menjadi anggota himpunan B? Atau sebaliknya? 

Yup, betul banget nggak ada kan? Nggak ada satupun anggota himpunan A menjadi anggota himpunan B dan begitu pula sebaliknya. Dalam hal ini dikatakan bahwa nggak ada anggota persekutuan antara himpunan A dan B. Maka, hubungan antara himpunan di atas disebut sebagai himpunan saling lepas atau saling asing. 

Contoh lainnya bisa elo liat pada gambar di bawah ini!

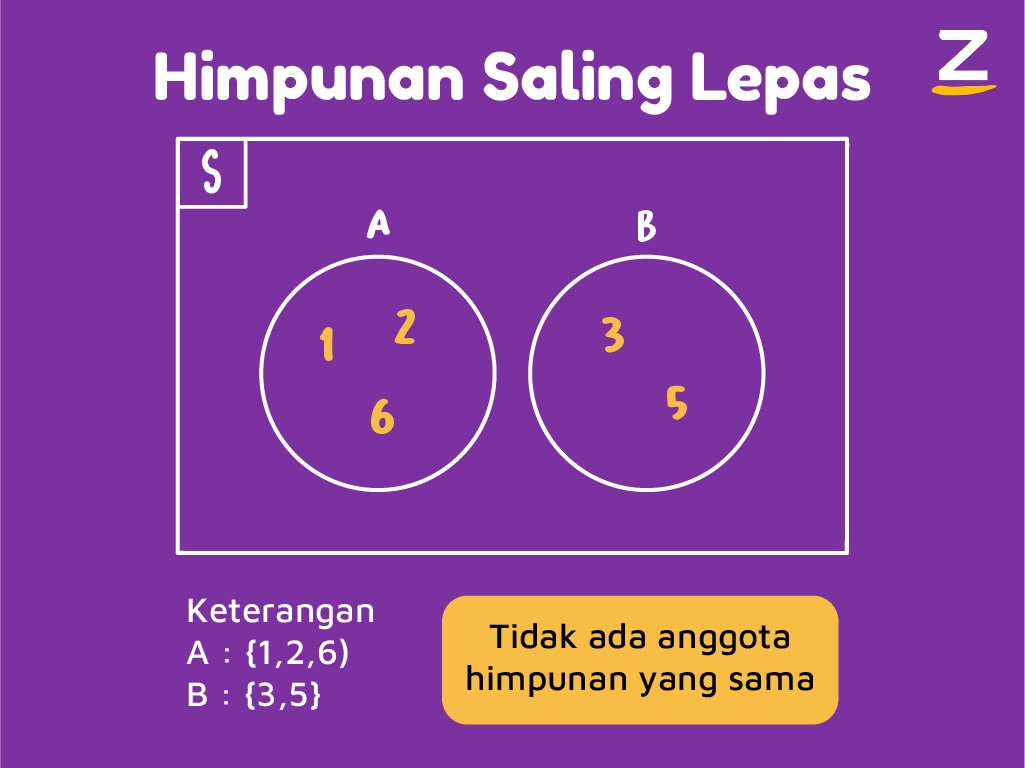
Gimana, guys? Udah mulai paham dong ya? Oke kita ke hubungan antar himpunan lainnya ya!

2. Himpunan Tidak Saling Lepas atau Himpunan Berpotongan

Setelah tadi ada himpunan saling lepas, sekarang ada lagi nih himpunan tidak saling lepas atau disebut juga himpunan berpotongan. 

Kayak apa sih himpunan tidak saling lepas itu?

Disebut sebagai himpunan saling lepas atau himpunan berpotongan karena ada anggota himpunan A yang juga merupakan anggota himpunan B. 

Tapi nih masih ada anggota A yang bukan anggota B, dan ada anggota B yang bukan anggota A. Elo bisa nulis himpunan ini dengan A ∩ B. 

Kayak gimana sih contohnya? Oke, biar jelas gue contohin ya!

Contoh:

A = {1, 2, 3, 4, 5} dan B = {2, 3, 5, 7, 11}

Coba elo perhatikan himpunan bilangan pada himpunan A dan B. Apakah elo melihat ada anggota himpunan A yang menjadi anggota himpunan B juga? 

Yup, bener banget, ada! Elo bisa lihat kalau himpunan pada himpunan A yang juga menjadi anggota himpunan B, yaitu {2, 3, 5}. 

Nah, dengan demikian bisa dikatakan kalau {2, 3, 5) adalah anggota persekutuan dari himpunan A dan B. 

Elo juga bisa lihat kalau masih ada anggota himpunan A yang nggak jadi anggota himpunan B, dan sebaliknya. Sehingga, hubungan antar himpunan tersebut disebut sebagai himpunan tidak lepas. Contoh lainnya bisa elo liat pada gambar di bawah ini ya!

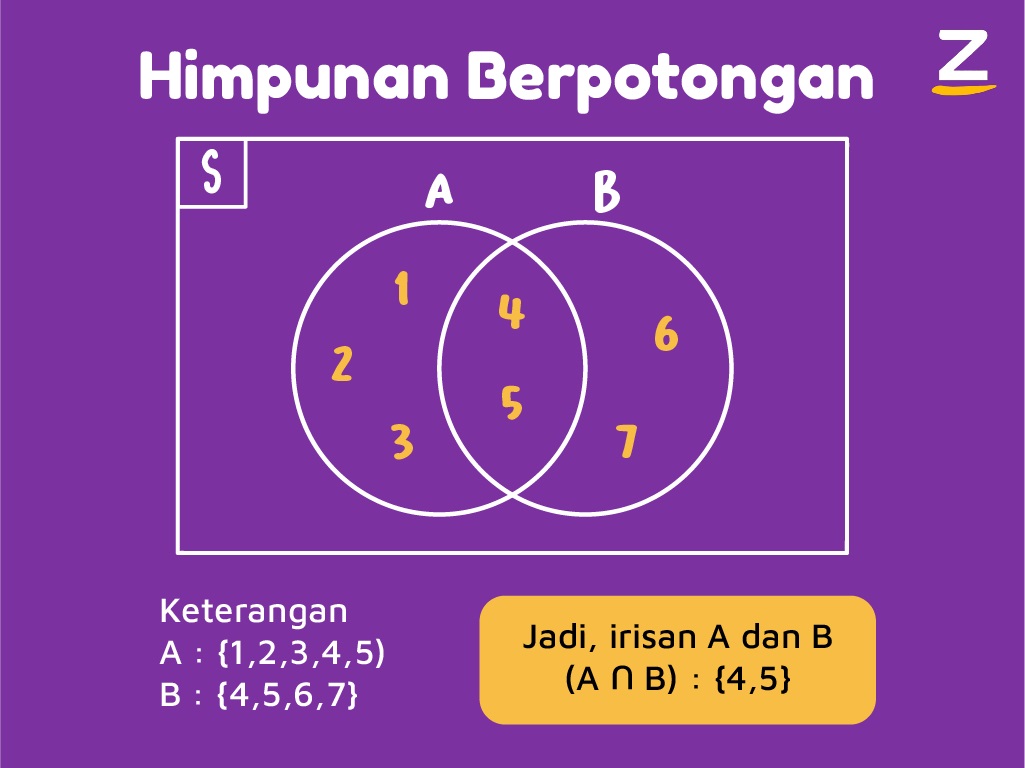
Baca Juga: 4 Macam Himpunan dalam Diagram Venn

3. Himpunan Sama

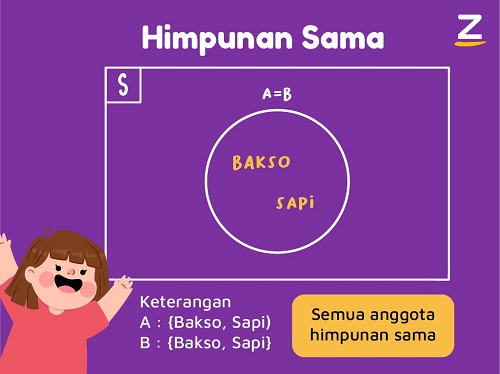
Himpunan selanjutnya adalah himpunan sama. Apa sih himpunan sama itu? 

Sesuai sama namanya, himpunan sama merupakan suatu himpunan yang sama. Maksudnya gimana sih? Jadi himpunan ini dikatakan himpunan sama ketika setiap anggota himpunan A merupakan anggota himpunan B juga, dan begitu pula sebaliknya. 

Penulisan hubungan antarhimpunan ini adalah A = B. Coba elo perhatiin contohnya di bawah ini ya!

Contoh :

A = {i, b, u} dan B = {b, u, i}

Elo bisa liat contoh himpunan di atas memiliki anggota himpunan yang sama. Setiap anggota A termuat juga dalam B, dan sebaliknya, meskipun urutannya nggak sama. Dalam hal ini, himpunan A dan B disebut dua himpunan sama, sehingga ditulis A = B.

4. Himpunan Ekuivalen

Himpunan yang terakhir yang akan gue bahasa adalah himpunan ekuivalen. 

Himpunan ekuivalen ini merupakan keadaan dimana terdapat banyak anggota dari kedua himpunan yang nilainya sama. Masih bingung nggak? Hehe … biar nggak bingung, gue kasih contohnya nih. 

Contoh:

A = {1, 2, 3, 4, 5} dan B = {a, b, c, d, e}

Dari himpunan di atas, elo bisa lihat kalau himpunan A mempunyai jumlah anggota yaitu n(A) = 5, sedangkan himpunan B mempunyai jumlah anggota yaitu n(B) = 5. Sehingga, (n(A) = n(B) = 5). 

Jadi, dapat dikatakan kalau himpunan A ekuivalen dengan himpunan B.

Gimana nih, udah paham belum tentang hubungan antar himpunan? Tenang aja, elo masih bisa belajar tentang materi ini dengan klik banner di bawah ini, biar elo makin tercerahkan!

Contoh Soal dan Pembahasan

Nah, biar pemahaman elo tentang materi ini makin oke, gue akan ngasih beberapa contoh soal hubungan antar himpunan dan pembahasannya. Yuk, simak ya!

1. Perhatikan himpunan berikut!

A: Mawar, Anggrek

B: Melati, Teratai 

C: Kenanga, Petunia

Menurut elo, jika dilihat dari himpunan yang ada, apa hubungan antar himpunan A, B, dan C?

Jawab: Himpunan Saling Lepas.

Pembahasan: 

Ketiga entitas di atas tidak memiliki anggota yang sama, masing-masing memiliki anggota himpunannya sendiri-sendiri. 

Dengan demikian, hubungan antar himpunan A, B, dan C adalah himpunan yang saling lepas. 

2. Perhatikan dua himpunan berikut!perhatikan dua himpunan berikut ini !

A = {2, 3, 5, 7, 9} 

B = {2, 3, 5, 8, 11}

Menurut elo, jika dilihat dari himpunan di atas, apa hubungan antar himpunan A dan B?

Jawab: Himpunan tidak saling lepas

Pembahasan: Dalam himpunan di atas, terdapat anggota himpunan A yang juga menjadi anggota himpunan B, yaitu {2, 3, 5}. Sehingga dapat dikatakan kalau {2, 3, 5} merupakan  anggota dari himpunan A dan B. 

Namun, masih ada juga anggota himpunan A yang tidak menjadi anggota himpunan B, sehingga keadaan tersebut disebut sebagai himpunan tidak saling lepas. 

3. Coba elo perhatiin gambar di bawah ini!

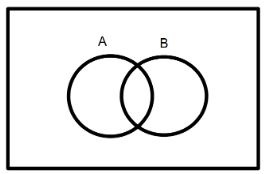
Berdasarkan gambar di atas, menurut elo manakah pernyataan di bawah ini yang sesuai dengan diagram Venn di atas?

A. A himpunan tari khas Sunda dan B himpunan tari khas Betawi.

B. A himpunan ikan dan B himpunan manusia.

C. A himpunan kopi dan B himpunan susu.

D. A himpunan sepatu sekolah dan B himpunan sepatu olahraga.

Jawaban: D. A himpunan sepatu sekolah dan B himpunan sepatu olahraga.

Pembahasan: Ada sepatu sekolah yang juga merupakan sepatu olahraga, atau sebaliknya, ada sepatu olahraga yang merupakan sepatu sekolah, sehingga terdapat irisan antara kedua himpunan tersebut.

Wah, selesai juga nih pembahasan kita tentang hubungan antar himpunan kali ini. Jangan lupa nih biar persiapan UTBK elo makin mantap, elo bisa banyakin kerjain tryout di sini 

Jangan lupa buat daftarin akun elo biar nggak ketinggalan info seru lainnya ya!

See you!

Baca Juga: 9 Kelebihan Try Out Online yang Bikin Siap Taklukkan Soal UTBK