Distribusi Peluang Diskrit - Materi Matematika Kelas 12

Di materi Matematika Kelas 12 ini, kita bakal bahas materi distribusi peluang diskrit. Selain itu, contoh soal distribusi peluang diskrit dan pembahasannya juga akan dijelaskan di sini. Ayo simak pembahasan selengkapnya!
Hai, Sobat Zenius! Gimana, nih, sama kehidupan elo di penghujung masa SMA ini? Hehe. Semoga semakin semangat ya! Entah yang mau lanjut kuliah, kerja, atau pun yang mau gap year terlebih dahulu.
Elo tahu nggak, sih, sama salah satu musuh Batman yang namanya Two-Face? Kalo elo belum pernah tahu sebelumnya, begini kira-kira penampakannya.

Nah, Two-Face ini sering banget mengambil keputusan dengan melempar koin. Jadi, misalnya kalau lagi laper, dia bakal bilang gini, “Pokoknya kalau yang keluar itu angka, gue bakal makan mi ayam, tapi gue bakal makan sate kalau yang keluar itu gambar.”
Ternyata, peluang Two-Face dalam mendapatkan angka atau gambar ini, bisa kita hitung menggunakan distribusi peluang diskrit. Oleh karena itu, yuk kita lihat pembahasannya lebih lanjut!
Peubah Acak
Materi ini berkaitan banget sama yang namanya statistika, yaitu percobaan-percobaan yang dilakukan akan menghasilkan suatu peluang.
Nah, peubah acak atau bisa juga disebut variabel acak, adalah fungsi yang memetakan ruang sampel ke himpunan bilangan real. Begini kira-kira.
f : S→R
Oh, ya, kalau dari hasil pemetaannya, peubah acak ini bisa dibedakan menjadi dua.
- Diskrit: memetakan ke himpunan bilangan diskrit
- Kontinu: memetakan ke himpunan bilangan real berupa interval
Kita ambil contoh dari hasil pemetaan diskrit, yuk!
Misalnya, nih, kalau kita melakukan percobaan melempar koin satu kali, bakal muncul di antara dua kemungkinan, yaitu angka (A) dan gambar (G).
S = {A, G}
Kita tentukan dulu, nih, peubah acaknya apa, misalnya angka (A).
X = banyak muncul angka
Oleh karena itu, A → 1 dan G → 0, sehingga X = {0,1}.
Oke, setelah kita bahas peubah acak, ayo kita lanjut ke distribusi peluang diskrit!
Baca Juga: Peluang Kejadian Saling Bebas – Materi Matematika Kelas 12
Distribusi Peluang Diskrit
Sebaran peluang (distribusi peluang) adalah fungsi yang memetakan peubah acak ke peluang yang berkorespondensi dengannya.
f : X → P
Berdasarkan peubah acaknya, distribusi peluang dibedakan menjadi dua.
- Diskrit (probability mass function)
- Kontinu (probability density function)
Nah, untuk pembahasan tentang distribusi peluang kontinu, elo bisa lihat lewat artikel di bawah ini.
Baca Juga: Pengertian Galat dan Contohnya dalam Kehidupan Sehari-hari – Materi Matematika Kelas 12
Oke, sekarang kita ambil contoh distribusi peluang diskrit, pada kejadian melempar koin dua kali. Begini ruang sampelnya.
S = {AA, AG, GA, GG}
Sekarang kita definisikan peubah acaknya.
X = Banyaknya muncul angka
X = {0, 1, 2}
Nah, bisa langsung kita masukin ke tabel, nih!

Di bawah ini, udah ada contoh soal yang bisa elo langsung kerjain, supaya makin ngerti dengan materi ini. Oh, ya pembahasan tentang distribusi peluang diskrit juga udah pernah dibahas di bawah ini. Sip!
Contoh Soal Distribusi Peluang Diskrit dan Peubah Acak
- Andi melakukan percobaan melempar 3 koin. Jika X = banyak muncul gambar, maka peubah acak dari percobaan tersebut adalah ….
a. X = {0}
b. X = {0,1}
c. X = {0,1, 2}
d. X = {0, 1, 2, 3}
e. X = {0, 1, 2, 3, 4}
2. Pada percobaan pelemparan dua buah koin dengan mata koin berupa angka (A) dan gambar (G). Diketahui X merupakan peubah acak munculnya angka pada kedua koin. Jika x adalah nilai pada peubah acak X, maka kejadian untuk x = 2 adalah ….
a. AG saja
b. GA saja
c. AG dan GA
d. AA saja
e. GG saja
3. Iyo melakukan percobaan melempar sebuah dadu. Diketahui peubah acak X menyatakan munculnya bilangan genap. Jika x adalah nilai pada peubah acak X, maka peluang kejadian saat x = 0 adalah ….
a. 0
b. ½
c. ⅓
d. ¼
e. ⅙
Pembahasan:
- Percobaan melempar 3 koin yang dilakukan Andi menghasilkan beberapa kemungkinan kejadian pada ruang sampel S yaitu:
S= {AAA, AAG, AGA, AGG, GAA, GAG, GGA, GGG}
Jika peubah acak X = banyak muncul gambar, maka kejadian yang mungkin:
- Muncul 0 gambar: {AAA}
- Muncul 1 gambar: {AAG, AGA, GAA}
- Muncul 2 gambar: {AGG, GAG, GGA}
- Muncul 3 gambar: {GGG}
Oleh karena itu, nilai peubah acak X = {0, 1, 2, 3}.
- Pada percobaan pelemparan dua buah koin dengan mata koin berupa angka (A) dan gambar (G).
Ruang sampel dari percobaan tersebut S = {AA, AG, GA, GG}.
Diketahui X merupakan peubah acak munculnya angka pada kedua koin.
- Muncul 0 angka: {GG}
- Muncul 1 angka: {AG, GA}
- Muncul 2 angka: {AA}
Oleh karena itu, X = {0, 1, 2}
Jika x adalah nilai pada peubah acak X, maka kejadian untuk x = 2 adalah kejadian muncul 2 angka pada dua buah koin yaitu AA.
3. Iyo melakukan percobaan melempar sebuah dadu. Ruang sampel kejadian pada percobaan tersebut S={1,2,3,4,5,6} dengan total 6 kemungkinan kejadian.
Peubah acak X menyatakan munculnya bilangan genap.
Muncul 0 bilangan genap: {1,3,5}
Muncul 1 bilangan genap: {2,4,6}
Maka, peubah acak X={0,1}.
Jika x adalah nilai pada peubah acak X, maka peluang kejadian saat x =0 adalah perbandingan banyaknya kejadian muncul 0 bilangan genap dengan banyaknya seluruh kejadian.
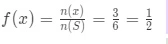
Oleh karena itu, peluang kejadian saat x = 0 adalah ½
Baca Juga: Pengertian Teorema Bayes dan Contoh Soalnya – Materi Matematika Kelas 12
****
Oke! Sekarang, gimana pendapat elo tentang materi distribusi peluang diskrit? Oh, ya, selain Matematika, elo bisa cari tahu lebih banyak tentang Fisika, Sejarah, Biologi, dan masih banyak lagi. Semuanya udah lengkap dan bisa diakses di sini secara GRATIS pake akun yang udah didaftarin di website atau lewat aplikasi Zenius. Selamat belajar!




