Siapa bilang rumus Matematika harus dihafal? Kamu juga bisa kok membuktikan rumusnya sendiri. Bagaimana caranya akan dijelaskan di sini.
Kalau lo belajar matematika, biasanya cara belajar lo itu gimana sih? Setau gue nih, cara belajar yang paling standard adalah: belajar teorinya, terus latihan soal. Kalau udah bisa ngerjain soal-soalnya, biasanya ngerasa udah ngerti sama materinya. Iya nggak sih? Tapi sadar nggak sih kalau sebenernya bisa aja lo nggak bener-bener ngerti sama materinya tapi tetep bisa ngerjain soalnya?
Gue sering banget nemuin kasus kayak gini. Jujur aja, ini nggak cuma gue temuin di anak-anak yang gue ajar. Tapi gue pernah juga nemuin ini di guru! Beneran. Guru. Ada beberapa orang yang pernah melamar untuk jadi guru di Zenius. Mereka sih bilangnya ngerti beberapa materi tertentu, tapi pas gue kasih beberapa pertanyaan mendasar, mereka nggak bisa jawab loh. Gue rasa kalau guru aja bisa ngerasa begitu, apalagi siswa yah.
Berdasarkan pengamatan gue terhadap beberapa siswa juga sama kasusnya. Ada siswa-siswa yang nilainya bagus di sekolah, tapi ternyata belum bener-bener paham sama konsep matematikanya. Kenapa bisa gitu? Karena banyak soal-soal ulangan yang sebenernya hanya menguji apakah elu:
- Hafal rumusnya
- Tau urutan ngerjainnya
- Bisa ngerjain pakai cara yang diajarin sama guru lo
“Yang penting kan gue bisa ngerjain soalnya. Dapet nilai lumayan juga pas ulangan”
“Ngapain sih pake pembuktian rumus segala? Ribet! Emangnya gue mau jadi matematikawan/wati!?”
Nah, kalau lo termasuk yang kayak gini, lo harus waspada nih. Karena kalau lo diuji dengan soal-soal yang menguji konsep, misalkan kayak soal-soal SBMPTN, bisa-bisa lo malah nggak bisa ngerjain. Coba deh lo perhatikan tipe soal-soal SBMPTN, konsep banget dan sangat beragam! Kalo lo terusin cara lo dengan ngandelin menghafal rumus, lo bakal ngos-ngosan.
Okay, terus kalau bukan latihan soal, gimana lagi dong belajarnya? Gue punya satu saran: Coba deh mulai sekarang, buktiin berbagai rumus matematika yang lo tau.
Gue kasih satu contoh. Misalnya gue punya soal kayak gini:
Soal di atas gampang banget lah ya, terutama kalau lo udah pernah belajar turunan. Mungkin lo udah tau trik ngerjainnya bahwa kalau ketemu x² diturunin jadi 2x, kalau ketemu x³ diturunin jadi 3x², dan seterusnya. Sehingga lo tau juga bahwa x⁷ itu turunannya adalah 7x⁶. Terus secara general, lo tau aturannya begini, untuk setiap:
Nah, sekarang bisa nggak lo buktiin, kenapa setiap xⁿ
turunannya adalah…
Buktiin bahwa itu berlaku untuk setiap n bilangan bulat dulu aja deh. Untuk bisa ngebuktiin ini aja, udah ada berapa konsep matematika tuh yang harus lo pahamin:
- Lo harus paham konsep bahwa turunan itu adalah limit untuk ∆x -> 0
- Lo harus tau gimana melakukan aljabar untuk limit-limit tak tentu
- Lo harus paham gimana menjabarkan (x+h)ⁿ
- Untuk bisa melakukan penjabaran di atas, lo harus ngerti segitiga pascal atau binomium Newton
- Lo harus terbiasa bekerja dengan banyak variabel (dan tau kapan harus mengabaikan beberapa hal karena ada yang bisa tercoret jadi nggak perlu lo tulis)
Kira-kira kebayang nggak gimana caranya ngebuktiin rumus di atas? Kalau lo bisa, coba kerjain dan posting hasilnya di comment section di bawah deh (foto aja coret-coretan lo terus upload ke sini).
So…. kalau untuk ngebuktiin satu rumus itu aja udah bisa bikin lo paham sama banyak konsep di matematika, gimana kalau lo bisa ngebuktiin 100 rumus coba? Pasti jadi jago banget deh. Hehehe….
While we’re at it, gue sekalian mau eksplor beberapa hal lagi nih, apa aja keuntungan dari berusaha membuktikan rumus matematika.
Keuntungan terbiasa membuktikan rumus matematika ini ngebantu banget buat kehidupan sehari-hari kita lho, dari ngebantu memecahkan masalah, memberikan kepuasan tersendiri, sampe ngebentuk mental kita supaya tahan banting. Manfaat-manfaat ini bisa dirasakan bahkan untuk kita yang tidak berprofesi sebagai matematikawan/wati.
Ah masa, sih? Ya udah yuk, kita langsung bahas aja.

Daftar Isi
Self-Explanation
Benefit pertama sebenernya lumayan jelas, yaitu self-explanation. Seperti contoh yang gue tunjukin di atas, dengan membuktikan satu rumus aja, lo sebenernya berusaha menjelaskan ke diri lo sendiri tentang gimana konsep yang lo pakai untuk membuktikan rumus itu.
Ada beberapa studi yang nunjukin kalau self-explanation itu bikin kita lebih cepet jago. Salah satunya studi di beberapa sekolah catur. Anak-anak di sekolah itu dikasih problem catur, terus minta bantuan komputer untuk memecahkan problem itu. Anak-anak yang disuruh menjelaskan kenapa langkah komputer begitu ternyata secara rata-rata jadi lebih jago dibanding anak-anak yang cuma mengamati langkah komputer itu. (de Bruin et al 2006)
Selain itu ada studi juga ke anak-anak kelas 9 yang lagi belajar beberapa teorema di Geometri. Pelajar itu dibagi menjadi dua grup, experiment group sama control group. Pelajar yang masuk ke control group belajar seperti biasa, sementara pelajar yang masuk experiment group dilatih untuk self-explain materi yang mereka pelajarin. Ketika mereka dites dengan soal-soal yang menguji konsep, ternyata pelajar di experiment group lebih bisa ngerjainnya dibanding pelajar di control group. (Wong et. al. 2002)
Jadi self-explanation ini memang terbukti efektif untuk bisa bikin kita ngerti sama materi yang lagi kita pelajarin. Btw, kalau lo doyan ngajar, ada studi juga yang nunjukin kalau mengajar juga bikin lo ngerti sama konsepnya. Sama efektifnya dengan self-explanation.
Ini juga nih, kalo lo mau ngetes diri lo apakah lo udah benar-benar paham mengenai suatu materi pelajaran, coba deh lo bantu ajarin teman lo yang belum ngerti. Di situ bakal kerasa banget, sebenarnya pemahaman lo udah sampe mana.
Intrinsic Motivation
Benefit berikutnya dari berusaha membuktikan rumus itu adalah lo bisa dapetin motivasi intrinsik dari belajar matematika. Kalau lo belum tau apa itu motivasi intrinsik, bagusnya lo baca dulu artikel gue tentang apa yang membuat seseorang termotivasi.
Berdasarkan pengalaman gue sendiri, waktu gue SMA, kalau gue berhasil ngebuktiin suatu rumus, langsung ngomong gini dalam hati, “Anjir ternyata gue jago!!!”. Hahaha… padahal sih sebenernya biasa aja, cuma gue betah aja ngutak-utik persamaan itu 3 hari berturut-turut sampe ketemu.
Respon gue rada lebay emang, tapi tetep Archimedes lebih lebay dari gue. Buat yang belum tau, Archimedes segitu senengnya nemuin gaya angkat Archimedes ketika dia lagi berendam di bak mandi, terus dia lari keluar kamar mandi dan teriak-teriak “Eureka!” di jalanan sambil telanjang.
Lo pernah nggak ngerasain seneng kayak gitu? Respon lo gimana? (boleh juga nih lo share di comment section). Well, apa pun bentuk respons lo, pastinya ada lah ya rasa seneng ketika lo berhasil. Menurut gue sih rasa senengnya melebihi rasa seneng ketika berhasil naik level ketika main game deh 🙂
Btw, ada studi juga tentang hal ini. Katanya, orang-orang yang terbiasa dapetin intrinsic motivation (rasa seneng) ketika belajar, ternyata gedenya jadi ketagihan untuk belajar. Terus, kalau lo lihat gimana perkembangan zaman sekarang ini, orang yang bisa survive itu bukan orang yang IPnya 4 atau nilai rapornya bagus aja, tapi orang-orang yang bisa secara konsisten mempelajari hal baru ketika nemuin tantangan baru.
Seriously, contohnya gini deh. Jaman dulu mana ada Twitter atau Facebook. Di kuliah 10 tahun yang lalu, mana ada yang belajar tentang Twitter atau Facebook sebagai media marketing? Tapi, sekarang zaman berubah; orang yang kerja di dunia marketing harus bisa adapt dengan cara mempelajari apa aja opportunity yang bisa didapet dengan Twitter dan Facebook.
Coba aja lo bayangin tantangan macam apa yang kira-kira akan lo dapet 10 tahun lagi? Kalau lo nggak doyan belajar, akan lumayan susah juga untuk beradaptasi sama perkembangan zaman.
Grit/Kegigihan
Benefit berikutnya lagi adalah Grit (kegigihan): ngebiasain diri untuk nggak gampang nyerah ketika lo ketemu tantangan. Ngebuktiin rumus itu bukan pekerjaan yang mudah. Ada kalanya beberapa menit aja bisa ketemu, tapi nggak jarang juga butuh beberapa hari. Ada quote yang menurut gue keren banget nih untuk ngegambarin ini:
“It’s not that I’m so smart, it’s just that I stay with problems longer” – Albert Einstein
Kegigihan ini penting banget loh untuk lo milikin, bukan cuma untuk ngerjain soal matematika doang, tapi untuk menyelesaikan persoalan di kehidupan lo juga (cieh).
Dalam beberapa tahun ke depan masalah lo itu lebih kompleks dari yang lo hadapi sekarang. Ya, lo bayangin aja beberapa tahun dari sekarang kira-kira persoalan apa aja yang mungkin lo hadapin? Bisa jadi lo bermasalah dalam menyelesaikan karya tulis ilmiah (skripsi), atau ada masalah dalam lingkungan sosial lo, percintaan lo, keluarga lo.
Bahkan mungkin juga lo akan menghadapi masalah keuangan yang harus lo atasi sendiri tanpa bantuan dari orang lain.
Itu baru persoalan-persoalan yang sifatnya pribadi. Gimana kalau lo punya visi besar nih; misalnya visi lo itu bisa menyelesaikan persoalan yang dihadapi banyak orang. Misalnya lo berkontribusi dalam penelitian medis, atau perubahan sistem pemerintahan suatu negara. Intinya lo punya niat baik untuk menjadikan dunia jadi lebih baik lah.
Semakin besar visi dan niat lo, berarti semakin besar juga dong kegigihan yang harus lo punya untuk bisa mencapai visi lo itu.
Mental Effort
Benefit berikutnya lagi nih… ngebiasain diri untuk ngasih mental effort yang besar setiap kali lo ketemu masalah. Kalau gue ditanya, “Apa musuhnya berpikir kritis?”, mungkin gue akan jawab, “Berpikir instan“.
Daniel Kahneman pernah ngegambarin bahwa cara berpikir manusia itu terbagi menjadi dua sistem: Sistem 1 dan Sistem 2. Sistem 1 itu adalah kondisi ketika kita berpikir secara intuitif yang nggak banyak menggunakan mental effort ketika berpikir, sementara Sistem 2 sebaliknya, kita berpikir menggunakan reasoning yang membutuhkan mental effort-nya sangat tinggi.
Kalau mau tau lebih banyak tentang ini, baca aja sendiri bukunya yah, judulnya Thinking: Fast and Slow. Di sini, gue jelasin singkatnya aja: untuk bisa berpikir kritis, lo harus bisa nempatin diri di sistem 2, biasain diri untuk memberikan mental effort yang besar setiap kali menghadapi masalah. Dengan begitu, lo akan seminimal mungkin terhindar dari berbagai kesalahan berpikir.
Contohnya, bisa nggak kejebak sama confirmation bias, nggak percaya gitu aja film Lucy yang bilang kita cuma make otak 10%, kritis soal aktivasi otak tengah, dan lain-lain.
The Beauty of Mathematics
Terakhir nih, pernah nggak sih lo ngelihat bukti-bukti matematika yang menurut lo elegan banget?
Buat orang-orang yang nggak pernah berusaha membuktikan persamaan matematika, mungkin nggak akan ngerasain bahwa pembuktian-pembuktian di matematika itu bisa keren banget. Tapi buat yang sering, pasti bisa mengapresiasi pembuktian-pembuktian matematika yang keren.
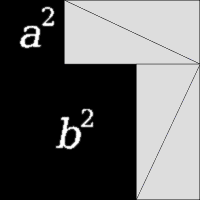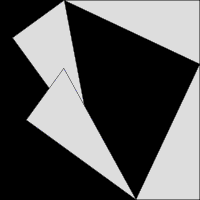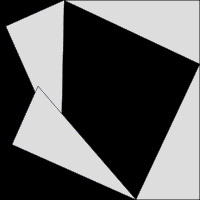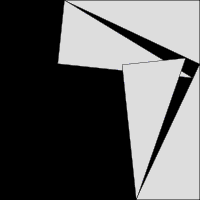
Kadang-kadang kita bisa bikin pembuktian matematis itu tanpa perlu nunjukin persamaan matematis, atau yang dikenal juga dengan “proof without words“. Contohnya, bukti Teorema Pythagoras dari gambar di samping ini.
Persamaan a² + b² = c² udah terbukti cukup dengan ngelihat gambar aja, nggak perlu nurunin persamaan panjang-panjang. Simple banget, dan elegan. Ini bahkan akan berasa lebih elegan lagi kalau lo pernah berusaha ngebuktiin Teorema Pythagoras pakai persamaan matematis yang jauh lebih ribet.
Yah, lo akan banyak nemuin pembuktian-pembuktian yang elegan kalau lo sering-sering latihan. Cobain aja. Cuma dengan begini lo bisa dapetin “The beauty of mathematics” itu.
Kira-kira Ini Membantu Persiapan SBMPTN Gue Juga Ngga, Ya?
Yup. Pasti ngaruh banget. Soal-soal SBMPTN itu banyak juga yang menguji konsep. Dengan lo berusaha membuktikan rumus-rumus matematika, pastinya ini membantu lo untuk memahami konsepnya, sehingga bikin lo lebih siap menghadapi soal-soal SBMPTN juga.
Justru nih menurut gue, mumpung lo lagi mempersiapkan diri untuk SBMPTN, bikin lah belajar lo ini jadi seru, jangan kering dengan cuma ngafal2in rumus aja. Baca juga tulisan Sabda yang ngomong bahwa perjalanan lo mempersiapkan SBMPTN ini ngaruhnya bukan cuma untuk lulus SBMPTN, tapi juga untuk jangka yang jauh lebih panjang dari itu.
Terus, Gue Harus Mulai dari Mana?
Well, lo bisa mulai dari mana aja. Bab apa yang sekarang lo pelajarin? Ada rumusnya, kan?
Nah… coba aja lo buktiin rumus yang ada di situ. Kalau lo nggak mau mulai dari situ, gue kasih beberapa list yang lumayan menarik untuk lo cobain deh:
- Buktiin semua rumus Trigonometri (rumus selisih, kali, penjumlahan, dll).
- Buktiin rumus ABC (rumus kecap) di persamaan kuadrat.
- Buktiin aturan sin dan aturan cos di segitiga dan vektor.
- Buktiin persamaan-persamaan lingkaran (persamaan garis singgung, jarak titik ke garis, dll).
- Buktiin teorema sisa di suku banyak.
- Buktiin aturan-aturan turunan yang selama ini lo hafalin.
- Buktiin rumus-rumus barisan dan deret aritmetika dan geometri.
- Dll
Sekalian boleh juga nih lo coba buktiin beberapa rumus Fisika berikut ini:
- Rumus-rumus kinematika gerak lurus (pakai konsep turunan dan integral).
- Rumus hambatan untuk rangkaian pengganti seri dan paralel.
- Rumus gelombang berdiri
- Dll
Okay, kira-kira itu aja sih hal yang mau gua sampaikan. Mulai sekarang gua tantang lo untuk mengubah cara belajar lo dengan selalu mengutamakan proses berpikir yang runut dan sistematis, salah satu cara yang paling konkrit ya, adalah dengan membuktikan rumus.
Dengan melatih cara belajar seperti ini, gua yakin akan berpengaruh juga ke banyak hal lain dalam kehidupan lo, terutama tentang gimana lo memandang suatu masalah dan memilih cara yang paling jitu untuk menyelesaikannya.
Referensi Gambar
Image credit: https://en.wikipedia.org/wiki/File:Pythag_anim.gif
Referensi Tulisan
Wong RM, Lawson MJ, and Keeves J. 2002. The effects of self-explanation training on students’ problem solving in high-school mathematics Learning and Instruction 12(2): 233-262
de Bruin ABH, Rikers RMJP, and Schmidt HG. 2007. The Effect of Self-Explanation and Prediction on the Development of Principled Understanding of Chess in Novices. Contemporary Educational Psychology 32(2):188-205
https://www.nobelprize.org/nobel_prizes/economic-sciences/laureates/2002/kahnemann-lecture.pdf
https://www.learningandthinking.co.uk/BK_PAUK_000214.pdf
Catatan Editor
Kalo ada yang mau ngobrol lebih lanjut sama Wisnu, jangan malu-malu langsung aja tinggalin comment di bawah artikel ini.
Sering nemu soal matematika yang sulit kamu jawab? Santai aja boy, nih kenalin ZenBot, temen 24 jam yang siap bantu kamu cari solusi dari masalah matematika! Untuk menjawab soal-soal tentang integral, kamu juga bisa manfaatkan fitur dari ZenBot, lho! Tanyain soal yang kamu gak bisa jawab lewat chat WhatsApp ZenBot sekarang atau download aplikasi Zenius versi Android dan iOS.











bang gue mau tanya,ngebuktiin integral gimana? wkwk
Rumus yang mana nih, yg integral x^n dx = x^(n+1)/(n+1) + c
Nih menurut perhintungan gue yg ngasal-ngasalan hahaha,
misal lu punya
y = x^3
dx^3 = 3x^2 dx
pindahin 3 nya
1/3 dx^3 = x^2 dx
integralin kedua ruas
integral 1/3 dx^3 = integral x^2 dx
1/3 x^3 = integral x^2 dx………..(persamaan a)
sekarang misalnya lu punya
y = x^4
dx^4 = 4x^3 dx
pindahin 4 nya
1/4 dx^4 = x^3 dx
integralin kedua ruas
integral 1/4 dx^4 = integral x^3 dx
1/4 x^4 = integral x^3 dx………..(persamaan b)
dilihat dari dua persamaan (a dan b), terbentuk pola dari hasil peng-integralan
jika x^2 di integral kan maka akan menghasilkan 1/3 x^3
jika x^3 di integral kan maka akan menghasilkan 1/4 x^4
dari data diatas, ditemukan bahwa pangkat nya bertambah satu, dan dibagi dengan pangkatnya
kesimpulannya, jika ada x^n di integralkan maka akan menghasilkan x^(n+1)/(n+1)
eaaaaaa……
Hehe.. masih belum bener bro. Soalnya lo baru nunjukin untuk x^2 sama x^3 aja. Belum bisa digeneralisir untuk x^n. Tapi usahanya boleh lah.
Wisnu OPS: Misalkan y = x^(n+1). Maka dy/dx = (n+1)*x^(n+1-1) atau dy/dx = (n+1)*x^(n). Kesamaan ini bisa ditulis sebagai dy/(n+1) = x^(n) dx. Integrasikan kedua sisinya, didapat [y/(n+1)]+C = integral x^(n) dx dimana C adalah konstanta integrasi. Tetapi y = x^(n+1). Maka hasilnya adalah:
integral x^(n) dx = [[x^(n+1)]/(n+1)]+C untuk n tidak sama dengan -1.
Jika n = -1, maka formula diatas menjadi:
integral 1/x dx = ln[nilai absolut dari x] + C, dimana ln adalah logarithm dengan basis e (sekitar 2,718) atau sering disebut dengan natural logarithm.
Sip. Itu pembuktian integral x^n memang tinggal lihat turunannya. Jadi dengan gitu aja lo udah dapet untuk n =/= -1.
Yang lebih mantab lagi kalau coba buktiin juga kenapa integral x^(-1) itu tiba-tiba muncul logaritma natural. Cuma ini materinya udah materi kuliah sih, karena urusannya sama bilangan e (euler).
Gampang. Pertama, kita buktikan bahwa d(e^x)/dx = e^(x). e^(x) dapat dinyatakan sebagai lim dari (1+(x/n))^n ketika n mendekati tak hingga. Setelah limitnya dievaluasi, e^(x) = 1+x+(x^2)/(2!)+(x^3)/(3!)+…, dimana e^(x) dapat dinyatakan sebagai deret pangkat tak hingga. Diferensiasikan suku demi suku, didapat d(e^x)/dx = e^(x). Kedua, buktikan bahwa d[ln(nilai absolut dari x)]/dx = 1/x. Misalkan y=ln[nilai absolut dari x]. Maka x=e^(y). Diferensiasikan kedua sisinya, didapat dx = e^(y) dy atau dy/dx=1/e^(y). Tetapi x=e^(y). Maka, dy/dx = d[ln(nilai absolut dari x)]/dx = 1/x. Karena integrasi adalah kebalikan dari diferensiasi, integral 1/x dx = ln[nilai absolut dari x] + C (Q.E.D).
Nice. Sebenernya lo mulai dari y = ln |x| dst aja udah cukup sih. Anggap turunan e^x udah tau. Berikutnya kalo buktiin turunan dari e^x, baru yg lo sebutin di atas, dan pakai definisi e yang deret juga cukup sih.
Btw, bilangan e ini punya 3 definisi yang berbeda. Lo udah sebutin tiga2nya. Nunjukin keterkaitan antara 3 definisi itu emang seru juga 🙂
Wisnu pasti banyak baca ya? Gw sudah terbiasa menulis bukti secara lengkap di mathematics. Makanya, gw buktikan dari derivatif fungsi eksponensial. Derivatif fungsi exponensial dan natural logarithm itu diajarkan di Zenius X tdk? Pingin tahu saja. Makasih.
Generalnya, diajarin sebatas yang pelajarin SMA aja. Tapi buat yang hobi sih, bisa diajak belajar hal yang lebih advanced dari itu. Ga cuma matematika digituin, ketika belajar yang lain-lain juga gitu.
Btw, kalau di matematika, yang namanya advanced itu bukan selalu berarti lebih kompleks atau apa ya. Kadang topiknya justru lebih mendasar. Contoh, buktikan bahwa 2+3=5. Pembuktian semacam itu sebenernya masuk kategori matematika yang rada advanced.
Beberapa penurunan formula dari list yang lu kasih
Itu upload dari gw, Ivan Alim, yg menggunakan nama guest.
Bagaimana caranya jika dibuktikan dengan induksi matematika?
tolong jelaskan ya teman…
Wisnu, ini ada beberapa penurunan formula dari list yang lu kasih dengan nama guest.
Sip. Mantab juga. Gue bahkan lupa kalau pembuktian untuk bilangan bulat positif dan negatif itu beda pas nulis artikel di atas 🙂
Deret maclaurin.=D
Benar sekali. Ekspresi seperti e^(x) = 1+x+(x^2)/(2!)+(x^3)/(3!)+… adalah contoh dari deret Maclaurin, dimana deret Maclaurin adalah kasus khusus dari deret Taylor. Secara umum, formula dari deret Taylor adalah f(x) = f(a)+[f'(a)/1!]*(x-a)+[f”(a)/2!]*(x-a)^2+[f”'(a)/3!]*(x-a)^3+… . Ketika a = 0, deret Taylor tereduksi menjadi deret Maclaurin f(x) = f(0)+[f'(0)/1!]*(x)+[f”(0)/2!]*(x)^2+[f”'(0)/3!]*(x)^3+… . Sudah belajar sampai deret Taylor di universitas ya?
Udah, kak. Kemarin baru belajar di Bab Barisan dan Deret pada Mata Kuliah Kalkulus 2. =D Nanti mungkin bertemu lagi di Metode Numerik.
Kalau gak salah, integral x pangkat -1 = lnx itu definisi kak Wisnu. Jadi gak perlu dibuktikan. =D CMIIW
Bisa, kan integral ada sejarahnya tuh, biar bisa menghitung luas benda tak beraturan dg akurat
Kalau enggak kan integral tuh anti derivatif, berarti asal muasalnya dr turunan, turunan asalnya dari limit. Soo? wkwk
Integral bukan dari turunan bro, asal muasalnya mereka independen, gaada hubungannya, yg satu nyari gradien, yg satu lagi nyari luas. Baru deh rada telat tiba2 orng nyadar kalo mereka saling berkebalikan
Integral yang mananya yang mau lo buktiin? Berhubung integral itu cuma anti-turunan (kebalikan dari turunan), berarti coba buktiin turunannya aja.
Misal, kalo lo bisa buktiin turunan x pangkat n itu n kali x pangkat n-1, berarti otomatis lo bisa buktiin kalau integral x pangkat n itu 1/(n+1) x pangkat n+1.
Kebanyakan pada ngejelasin integral itu pake rumus anti-turunan (fundamental theorm of calculus). Padahal originalnya dari riemann sum, trus pake kombinasi limit dan deret baru bisa ketemu luas kurva nya
Iya bang bener banget kalo bisa sampe ngerti ngebuktiin rumus itu jadi ada kerasa yang waw gitu. Kadang kalo gua lupa rumus aja jadi balik ke konsep awal lagi.
Nah… itu dia. Gue dulu waktu SMA juga gitu. Bahkan hal-hal simple kayak berapa sin 30 aja gue kadang suka lupa pas ngerjain soal. Tapi berhubung tau nuruninnya dari mana, yaudah, turunin aja lagi dari konsep dasarnya.
kenapa di SMA ga diajarinnya kaya gini wis?
Kebanyakan sekolah biasanya cuma ngandelin nilai sih untuk memotivasi anak2 belajar. Jarang banget yang ngandelin intrinsic motivation dalam mempelajari ilmunya, jadi belajarnya ga seru.
Berpikir kreatif itu agak susah didefinisiin. Tapi kalau artis (pekerja seni) lagi kerja keras, misalnya melukis atau bikin lagu, sebenernya itu masuk sistem 2 juga sih. Kalau lihat aktivitas otaknya ketika mereka berkarya, pastinya aktivitasnya tinggi juga.
kenapa susah didefinisiin?? (kasi contoh kasus)
kalo kata gw berpikir kreatif = (secara sempit) lebih ke berpikir analogis
Susah itu karena scientist aja ngedefinisiinnya beda2. Cek di wikipedia deh:
http://en.m.wikipedia.org/wiki/Creativity
Definisi generalnya begini:
“Over the course of the last decade, however, we seem to have reached a general agreement that creativity involves the production of novel, useful products”
Tapi kalau baca bawah2nya lagi, konsep tentang kreativitas yang pernah diusulin sama berbagai scientist itu lumayan beragam.
Wisnu, ini ada beberapa penurunan formula dari list yang lo kasih
Wisnu, ini ada beberapa penurunan formula dari list yang lu kasih:
ngaruh juga buat yang mau ikut olimpiade fisika sma. soalnya konsep banget, tiap hari disuruh buat rumus sendiri wkwk
Bikin rumus sendiri terus kalau ketemu ditulis-tulis pembuktiannya di jendela kah? :p
Film apa nih bang ???
“a beautiful mind” i guess?
Keren banget, bang! Sumpah!
Thanks 🙂 Dasarnya cuma kemampuan matematika sebelumnya sih. Misal, untuk membuktikan trigonometri, lo butuh kemampuan dasar tentang kesebangunan segitiga. Untuk membuktikan integral, harus ngerti turunan. Dsb.
ikutan nyimak ah biar dapet ilmu.. 😀
Streaming Net TV
bang wisnu, gw kan maba nih, dan ternyata untuk semester awal ini, gw nemu lagi pelajaran sma (fisdas, kimdas, matematika (dasar & ipa), sama biologi umum)..
nah kan wkt gw masuk kelas matematiknya gw ngerasa gk fun gitu bang.. padahal wkt sma (walau gk jago mungkin kurang) gw ngerasa asik aja gitu ngutak ngatik angka.. terus untuk ngimbangin belajar kyk gini (sense of beuty-nya matematik) kan pasti harus butuh wkt yg lumayan tuh, sedangkan tuntutan dunia kuliah tuh banyak bang apalagi tugas2nya, gmn ya ngatasinnya (supaya tugas kelar dan ngerti juga)??
Yup. Gue juga pernah ngerasain hal yang sama sih. Solusinya biasanya gini: Belajar pakai textbook kuliah yang direkomendasiin sama dosen (biasanya textbook itu tertulis di silabus), jangan belajar dari catatan kuliah atau slides presentasi dari dosen. Gue udah berkali-kali lihat anak-anak kuliah sekarang lebih banyak belajar dari slides presentasi power point gitu. Menurut gue itu useless, apa lagi kalau ilmunya ilmu2 dasar kayak Kalkulus, Fidas, Kidas, etc. Jauh lebih bagus kalau baca dari textbook sih.
Punya akses ke perpus kan? Tongkrongin aja perpusnya, baca di sana 🙂
sipdeh bang, thanks … dicoba sarannya.. (y)
oh iya, kalo boleh sih, zenius ada bagian buat yang kuliah juga dong.. kan lumayan buat yang masih belajar matkul dasar sama yang emang ingin memperdalam ilmunya..
sipdeh zenius.
awesome …..bang, ada gk buku atau artikel tentang konsep matematika secara sederhana buat anak SMA ? kalau ada sebutin yaa. THANKS…..
Bagus sih klo punya effort yang tinggi buat ngebuktiin rumus, tapi saking penasarannya, gue kadang pusing sendiri, hal yang mudah malah jadi sulit saking pengennya ngebuktiin tuh rumus? Itu gimana dong? Apa mungkin insight gue masih kurang ya?
top, zenius paling ok !!! 🙂
bang mau nanya, hbs di buktiin gitu kan rumusnya, cara penggunaan pembuktian rumus itu buat soal sbm caranya gimana?
Kak aku kan sering buktiin rumus matematika gitu, dan guru aku juga metodenya sering nyuruh kita presentasi gitu kalau ada bab yang mesti di diskusikan. Tapi kak waktu sbmptn dan un kan dituntut masalah waktu kak, seringnya nih satu soal selesainya bisa dapat jawabannya setengah jam. Kebayang kan gimana kita mau tes tapi nemu jawaban lamaaaaa banget. Gimana caranya kak supaya bisa pakai semua konsep yang kita punya di tempat yg tepat dan dengan waktu yang tepat? Apa banyak latihan aja cukup ? Atau kita butuh hafalin rumus cepat ala bimbel juga beside paham konsep?
gue skrg kuliah di jurusan matematika mipa. membuktikan rumus ini emang jadi kerjaan sehari2 bgt (walaupun baru seminggu kuliah, hehe) apalagi kalkulus. tapi bang, gue masih bingung klo mau buktiin rumus itu mulainya darimana. misalnya, gue tau 1+1=2. oke gue mau buktiin. tapi, harus mulai darimana? mulai dari konsep/teorema apa? mohon bantuannya bang 🙂
Maaf kak. Itu video yang ada di dalam link list pembuktian itu bisa di download gk? Gimana caranya? Aku pengin nonton tp gk bisa streaming
kak gue mau nanya untuk pembuktian dari aritmatika sosial gimana yaa?
gokil, Sabda sering banget ngulang-ngulang itu rumus “kecap” gokil gokil gw baru nyadar maksudnya “kecap” tuh hahay, asiklah gw udah mulai dengan satu pembuktian yesss :’D
baru nurunin rumus diagonal bidang, diagonal ruang, luas, panjang total dari kubus sama balok :’) :3
wisnu kata kamu di video fluida statis kls 10 klo batu yg sama di jthkn dri udara ke tanah sama dari udara ke air lebih cepat yang ke air karena ada gaya apung keatas(dri ktinggn yg sama) . bukanya klo gaya apung ketas berarti batunya yang semula gaya kebawah doank jdi berkurang karena ada gaya keatas
@@wisnuops:disqus
Bang Wisnu, gue bisa nih nurunin garis singgung lingkaran yang pusat (a,b). Setelah pelajarin konsepnya dari lo bang, yeay. Thanks bang Wisnu.
Cmiiw
Sorry kalo berantakan bang hehehe
Berikut adalah penurunan pers. garis singgung lingkaran berpusat di [a,b] dengan jari-jari R untuk titik [x1,y1] yang terletak pada lingkaran.
Wisnu, ini ada penurunan rumus Einstein yang terkenal itu: E=mc^(2). Penurunan rumusnya keren ya.
btw iq nya brpa kak?
*pengen tw aja
Gue tidak tahu. Menurut gue, IQ itu tdk penting. Yang lebih penting adalah rasa keingintahuan untuk selalu belajar serta menikmati apa yang kita pelajari.
menurut saya banyak kesalahan pengajar itu adalah membiarkan siswa belajar sendiri, sekolah itu dibayar untuk mengajarkan kita, bukan untuk membuat kita belajar sendiri, kalau belajar sendiri buat apa ada sekolah? trus bagi siswa menjadi 3: sedikit paham, setengah paham, paham. pisah kelompok mereka, pengajaran juga terbagi 3 bagian tersebut diatas, guru dan dosen semua pukul rata semua siswa,(yang terjadi ya tau sendiri..) bahkan maaf untuk sekelas program magister ITB, mahasiswa banyak belajar sendiri dan kewalahan terhadap tugas, tugas dan tugas. melelahkan pikiran, badan dan otak.., anehnya, kita bayar mahal ke sekolah kita sendiri yang pusing, aneh kan ?!! sekolah itu justru membuat otak kita tidak pusing. ini justru 360 derajat terbalik.
maaf saya datang kesini karena sampai pukul 01.00 masih berusaha membuktikan sebuah rumus yang saya tidak tau sendiri bagaimana? oh tuhan…
Jujur aja nih ya, gue gatau cara belajar konsep tuh gmna? caranya nurunin rumus kah? Atau gmn?
Cool. It was a couple days ago when I watched “the man who knew infinity” and today came across this blog (pembuktian matematika) for high schollers. Man, it maybe true that we talk the same language.
klo fisika bisa ga kak banyak cara gtu kak? :’)
Bisa juga kok. Di atas ada contohnya juga kok untuk yang Fisika.
Fisika itu sebenernya banyak rumus turuannya. Setiap kali kita belajar suatu bab, biasanya rumus dasarnya cuma dikit banget. Contoh, kalau belajar Mekanika Newton, rumus dasarnya cuma 3 (Hukum Newton 1, Hukum Newton 2, dan Hukum Newton 3). Tapi rumus aplikasinya bisa segudang.
Tadinya gua byk nanya dikelas tp akhirnya temen2 dan guru gua jd risih sendiri sama pertanyaan “itu kenapa bisa gitu bu? Dapet darimana?” Wkwk.. And akhirnya gua coba sendiri di rumah, gua ngebuktiin persamaan kuadrat dengan nurun”in rumusnya. Dan ternyata jadi enak ngerjain soalnya.. Bisa pake cara kutak-katik sesuka kita, cara paling nyaman buat ngerjain aoal2 itu pake versi nyamannya kita.. Dipelajaran lain gua jg suka bingung terutama fisika, but untung gua gua beli zenius jadi tau basic dasarnya ^^