Teka-teki Matematika – Dua Kereta

Suka teka-teki matematika? Coba pecahkan teka teki tentang dua kereta yang bergerak berhadapan dengan pergerakan burung di antara dua kereta tersebut.

Kali ini, gue mau iseng-iseng bahas satu teka-teki matematika yang umurnya udah lumayan tua juga. Seinget gue, teka-teki ini udah ada sejak ratusan tahun yang lalu. Tapi sayangnya, setelah gue googling-googling, gue belum ketemu juga siapa yang pertama kali bikin ini. Langsung aja, teka-tekinya gini.

“Ada dua kereta, berjarak 800 meter satu sama lain saling berhadapan. Masing-masing bergerak dengan kelajuan 10m/s. Di depan kereta yang pertama, ada burung yang bergerak dengan kelajuan 20m/s menuju kereta yang ke dua. Ketika burung tersebut sampai di kereta yang ke dua, dia langsung berbalik arah seketika lalu bergerak dengan kelajuan 20m/s lagi menuju kereta yang pertama. Ketika sampai di kereta yang pertama, dia langsung berbalik arah seketika lagi lalu bergerak dengan kelajuan 20m/s lagi menuju kereta yang ke dua. Dan seterusnya sampai kedua kereta tersebut bertabrakan.”

Biar lebih jelas, lihat animasinya di bawah ini deh..

Jarak kedua kereta = 800m

Kelajuan Kereta A = 10 m/s

Kelajuan Kereta B = 10 m/s

Kelajuan Burung = 20 m/s

Pertanyaannya: Berapa Jarak Yang ditempuh oleh burung?

[NOTE: SEPERTI BIASA, KALAU ADA SOAL-SOAL BEGINI, JANGAN LANGSUNG LIHAT JAWABANNYA, TAPI COBA LO PIKIRIN BENER-BENER DULU GIMANA CARA NGERJAINNYA]

Udah dicoba? Oke, kebayang nggak sih lo ngerjainnya gimana?

Ada beberapa macam cara ngelihat soal ini nih sebenernya. Waktu gue masih SMA, gue inget banget ngelihat soal ini pas lagi belajar deret. Terus gue coba kerjain aja pakai konsep deret geometri tak hingga.

Loh kok pakai deret geometri tak hingga? Kenapa?

Nah, ini salah satu kerennya deret tak hingga. Kebayang nggak sih lo kalau ada suatu barisan yang sukunya tak hingga, tapi jumlah semua sukunya berhingga. Sekarang coba lihat lagi lintasan burung tadi. Perhatiin bahwa:

1. Si burung akan bolak-balik dari kereta 1 dan kereta 2 sebanyak tak hingga kali
2. Total lintasan burung itu berhingga

So, ini contoh yang pas banget untuk soal deret tak hingga. Nanti kita juga bisa ngelihat kalau jarak tempuh burung itu pada tiap lintasan itu merupakan barisan Geometri.

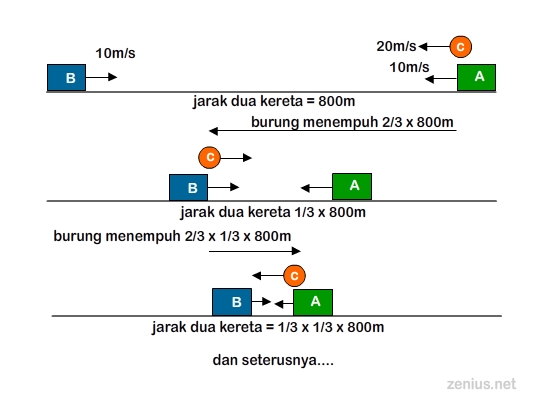
Sekarang kita lihat gambar lintasan burungnya dulu….

Dari gambar ini, kelihatan kalau jarak yang ditempuh burung tiap lintasan itu begini:

1. Lintasan Pertama

Jarak yang ditempuh Burung pada lintasan pertama:

$$ U_1 = \frac{2}{3} \times 800 $$

2. Lintasan Ke dua

Jarak yang ditempuh Burung pada lintasan ke dua:

$$ U_2 = \frac{2}{3} \times \frac{1}{3} \times 800 $$

3. Lintasan Ketiga

Jarak yang ditempuh Burung pada lintasan ke tiga

$$ U_3 = \frac{2}{3} \times \frac{1}{3} \times \frac{1}{3} \times 800 $$

… dan seterusnya sampai tak hingga

Nah, kelihatan banget kan kalau ini sebenernya adalah deret geometri tak hingga dengan suku pertama $$ a = U_1 = \frac{2}{3} \times 800 $$ dan rasio $$ r = \frac{1}{3} $$. Berarti kalau gitu menghitung jumlah seluruh lintasan gimana? Tinggal dijumlahin aja kan semuanya. Gini:

$$ S_{\infty} = \frac{a}{1-r} $$

$$ S_{\infty} = \frac{\frac{2}{3} \times 800}{1-\frac{1}{3}} $$

$$ S_{\infty} = \frac{\frac{2}{3} \times 800}{\frac{2}{3}} = 800m $$

Done!!! Ternyata jawabannya 800 meter!

Waktu SMA sih, gue lumayan puas setelah berhasil menghitung ini, terus gue lanjut ngerjain yang lain. Tapi, gue inget pas kuliah tingkat-tingkat awal, somehow gue ketemu lagi sama problem ini, terus baru ngeh kalo ada solusi yang jauh lebih simple.

Cara yang lebih simple

Kepikiran nggak sih kalau sebenernya waktu tempuh burung itu kan sama dengan waktu tempuh kedua kereta. Waktu yang dibutuhkan kedua kereta untuk bertabrakan bisa dihitung:

$$ t = \frac{jarak total}{v_1 + v_2} = \frac{800}{10+10} = 40 detik $$

Kalau gitu jarak yang ditempuh burung tinggal langsung dihitung aja

$$ d = v_{burung} \times t = 20 \times 40 = 800 m $$

Selesai… Ketika gue nemuin cara ini, gue inget rada ngedumel dalam hati, “Sial cuma gini doang!”. Hahaha…

Jebakan matematika

Soal matematika emang kadang bisa bikin gregatan kayak tadi sih. Udah nyari susah-susah, eh ternyata baru sadar setelah itu kalau ada cara yang lebih simple, dan kadang lebih elegan. Tapi lo jangan nganggap bahwa ngerjain soal dengan cara yang panjang itu jelek juga. Justru seringnya kita memang perlu melalui proses ngerjain soal dengan cara kayak gitu dulu sebelum akhirnya ketemu cara yang lebih elegan. Belajar dengan cara kayak gitu sama sekali nggak ada salahnya. Itu masih jauh lebih baik dibanding belum apa-apa udah nyerah duluan, terus malah nggak nyobain sama sekali. Iya nggak sih?

Bahkan konon katanya John von Neumann (1903-1957) pernah dites sama soal ini terus dia jawab cepet banget. Orang yang nanya langsung ngerespon, “Oh, you must have heard the trick before!”. Terus Neumann bales, “What trick? All I did was sum the infinite series.” Hehe… Bahkan, orang sejago Neumann aja ngerjainnya pakai deret geometri tak hingga kok.

Kalau Matematika SBMPTN atau ujian lainnya gimana? Kan itu harus cepet ngerjainnya

Nah, ini emang bener. Lo emang harus ngerjain SBMPTN atau soal ujian lain dengan waktu yang terbatas. Tapi justru itu ketika lo belajar (sebelum ujian), lo harus berusaha keras ngerjain berbagai soal. Nggak apa-apa kalau lo awalnya ngerjain dengan cara yang panjang. Berikutnya lo tonton pembahasan di Zenius supaya ngerti konsepnya. Semakin lo terbiasa nerapin dari konsep ke aplikasi, lo akan semakin inget sama konsep dasarnya, dan semakin mahir pula untuk nerapin konsep dasar itu ke berbagai aplikasi yang mungkin. Nanti soal-soal yang dulunya lo anggap susah, lama-lama dikedipin aja selesai.

Barisan dan deret

Balik lagi ke Barisan dan Deret. Di awal, gue nunjukin kalau soal ini bisa dikerjain dengan konsep deret geometri tak hingga. Kalau lo ngerasa belum ngerti tentang konsep barisan dan deret ini, lo bisa tonton video di zenius.net tentang barisan dan deret, di sini: Barisan dan Deret

***

Okay, sekian teka-teki matematika dari gue. Coba aja lo iseng-iseng tantangin teka-teki ini ke temen-temen lo, terus lo jelasin ke mereka gimana cara lo ngerjainnya. Minimal pakai dua cara di atas ya! 🙂 Bahkan kalau perlu lo diskusiin ini juga sama guru lo. Okay, deh… gitu aja… We’ll come back with more puzzles for you next time!

[Catatan Editor : Btw kalo lo punya teka-teki matematika yang lo tau, boleh nih lo share ke kita dengan tulis teka-tekinya di comment bawah, biar nanti kita coba bahas dan ulik bareng-bareng . Kalo lo mau ngobrol langsung sama Wisnu, bisa langsung tinggalin comment  di bawah artikel ini aja.  Pastiin juga lo dapetin membership zenius.net buat bisa akses seluruh video materi dan pembahasan soal UN Matematika maupun soal dan pembahasan SBMPTN tahun-tahun lalu]