Rumus dan Cara Menentukan Titik Stasioner – Materi Matematika Kelas 11

Kalau elo sudah belajar tentang persamaan fungsi garis singgung, elo pasti akan menemukan satu titik di mana fungsi “berhenti” naik atau turun. Titik ini disebut sebagai titik stasioner.

Nah, apa sih sebenarnya titik ini? Bagaimana cara menentukan titik stasioner?

Kita pelajari bareng-bareng, yuk!

Apa Itu Titik Stasioner?

Titik stasioner merupakan sebuah titik dalam grafik yang turunan kurva pertamanya sama dengan nol. Titik ini disimbolkan dengan rumus berikut:

Supaya lebih mudah dipahami, titik stasioner dapat digambarkan dalam garis fungsi seperti gambar di bawah ini.

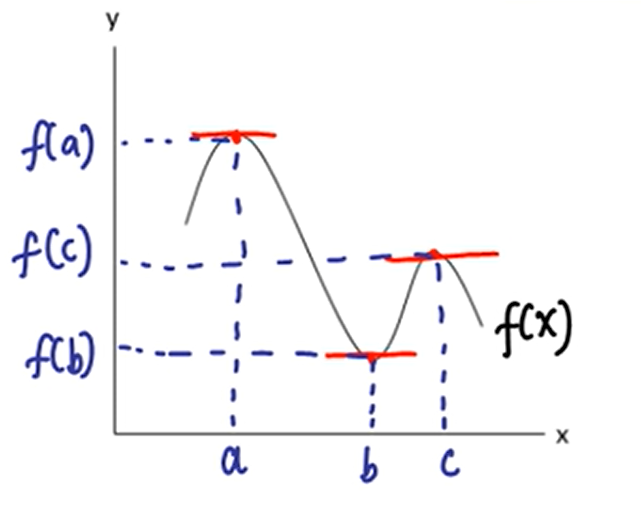
Pada garis fungsi ini, elo bisa menemukan tiga titik. Pertama, pada saat nilai x=a, sehingga fungsinya disebut sebagai f(a). Kemudian, titik stasioner selanjutnya muncul saat nilai x=b, fungsinya disebut sebagai f(b). Lalu yang terakhir muncul saat nilai x=c, sehingga fungsinya adalah f(c).

Oleh karena itu, titik stasionernya adalah:

• (a, f(a))
• (b, f(b))
• (c, f(c))

Elo juga bisa menyebut bahwa nilai stasionernya adalah:

• f(a)
• f(b)
• f(c)

Baca Juga: Rumus Persamaan Garis Singgung dan Contoh Soal – Materi Matematika Kelas 11

Cara Menentukan Titik Stasioner

Lalu, bagaimana cara menentukan titik stasioner? Coba ikuti contoh soal berikut.

Tentukan titik stasioner fungsi berikut:

Ingat, nilai fungsi dari titik stasioner harus sama dengan nol (f’(x)=0). Sehingga, turunan dari fungsi ini adalah:

Sehingga, elo mendapatkan nilai x:

Sekarang, elo hanya perlu menentukan nilai f(x) untuk mendapatkan titik stasioner dengan memasukkan nilai x. Pertama, elo harus mencari nilai fungsi f(-3).

Berarti pada fungsi f(-3), titik stasioner ada pada titik (-3,31). 

Selanjutnya, cari nilai fungsi f(1).

Artinya, pada fungsi f(1), titik stasioner ada pada titik (1,-1).

Baca Juga: Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11

Contoh Soal Titik Stasioner

1. Perhatikan grafik berikut:

Titik-titik stasioner ditunjukkan pada titik ….

a. A dan E

b. A, C, dan E

c. B, C, dan D

d. A, B, C, dan E

e. A, B, D, dan E

Titik stasioner diperoleh ketika fungsi gradien garis singgungnya bernilai nol. Dengan kata lain, titik-titik di mana gradien garis singgungnya sejajar dengan sumbu -x−x, yakni di titik-titik B, C, dan D. Jawabannya adalah c.

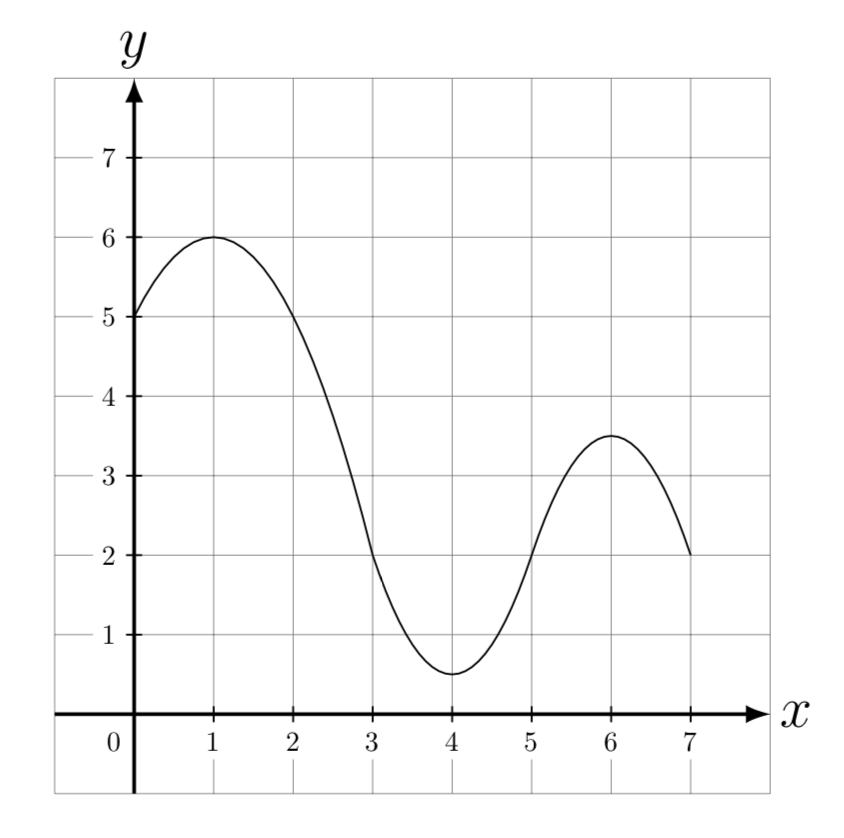
2. Salah satu nilai stasioner pada grafik berikut ini adalah ….

a. 5

b. 6

c. 4 ½ 

d. 4

e. 1 ½

Nilai stasioner adalah nilai y dari titik stasioner. Dari gambar, dapat dilihat bahwa titik-titik stasionernya adalah (1,6), (4,½), dan (6,3½). Jadi, nilai stasionernya adalah 6, ½, dan 3½. Pada pilihan jawaban yang tersedia, jawaban yang benar adalah b. 6.

3. Tentukan titik stasioner dari fungsi berikut.

a. (2,4) dan (-1,31)

b. (-2,4) dan (1,31)

c. (-2,20) dan (1,11)

d. (2,20) dan (-1,11)

e. (2,20) dan (1,11)

Ingat, titik stasioner ada ketika nilai f’(x)=0. Sehingga,

Maka, nilai x adalah x=2 atau x=-1. Kemudian, elo harus memasukkan nilai x untuk menentukan titik y.

Jadi, elo menemukan titik stasionernya adalah (2,4) dan (-1,31). Jawaban yang benar adalah a.

Baca Juga: Sifat & Rumus Integral Tak Tentu – Materi Matematika Kelas 11

Bagaimana, apa elo sekarang sudah paham bagaimana cara menentukan titik stasioner? Untuk pemahaman lebih lanjut, elo bisa mempelajarinya dari materi yang ada di aplikasi Zenius dengan cara klik banner di bawah ini.