Halo, Sobat Zenius! Apakah elo sudah mulai belajar tentang definisi, jenis, dan rumus dari transformasi geometri kelas 11? Elo masih ingat dengan jenis-jenis transformasi kan? Ada translasi, refleksi, rotasi, dan dilatasi. Kali ini gue akan sharing, bagaimana jenis-jenis tersebut dibawa ke dalam bentuk matriks.

Kalau diuraikan tiap katanya, “transformasi” artinya perubahan rupa, dan “geometri” berarti cabang ilmu matematika yang mempelajari sifat garis, sudut, bidang, dan ruang. Jadi, secara umum transformasi geometri adalah perubahan rupa yang dilihat dari garis, sudut, bidang, dan ruang.

Contohnya saat elo bercermin, ada diri yang asli dan ada bayangan elo di cermin. Nah, kalau dalam ilmu ini, posisi awal (misalnya diri elo saat bercermin) adalah (x,y), sedangkan posisi akhir (diri elo di dalam cermin) dinotasikan dengan (x’, y’).

Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 113 — Contoh aplikasi transformasi geometri (*dok. Giphy)*

Dalam materi transformasi geometri kelas 11 kali ini, gue nggak akan membahas pengertian dan contoh dari jenis-jenis tersebut secara detail, karena itu udah dibahas di artikel sebelumnya di sini.

Daftar Isi

Matriks Translasi

Translasi atau pergeseran merupakan perpindahan suatu titik sepanjang garis lurus. Jadi, si titik itu hanya digeser atau dipindah tanpa diputar atau mengubah ukurannya. Sama halnya ketika di kelas elo ada aturan geser tempat duduk setiap seminggu sekali.

Elo hanya bergeser tempat duduk tanpa mengubah arahーyang awalnya menghadap papan tulis menjadi membelakangi papan tulis, nggak gitu kan konsepnya? Dan ukuran tubuh elo tetap dengan ukuran seperti itu, gak tiba-tiba baru pindah langsung mengecil atau membesar, nggak kan?

contoh transformasi geometri translasi dengan matriks zenius — contoh transformasi geometri translasi dengan matriks

Dari gambar di atas, kita bisa tau nih kalau posisi awal elo duduk ditandai dengan A, sedangkan posisi elo di tempat duduk baru ditandai dengan A’ (A aksen). Sekarang coba tentukan titiknya dilihat dari garis koordinat di atas.

A(1,1) → A’(1+4,1) = A’(5,1)

Sekarang kalau duduknya geser ke belakang, selama masih berada pada sepanjang garis lurus, maka tetap dikatakan sebagai translasi. Berarti akan diperoleh hasil pergeseran ke tempat duduk di belakang, yaitu:

A(1,1) → A’(1,1+2) = A’(1,3)

Dari ilustrasi di atas, diperoleh konsep dan rumus dari transformasi geometri dengan matriks translasi yaitu suatu titik A(x,y) digeser atau ditranslasi sejauh T(a,b)ーa (kanan-kiri) atau b (atas-bawah)ーakan menghasilkan A’(x+a, y+b) atau A’(x’,y’).

x’ = x+a

y’ = y+b

Nah, x’ dan y’ itulah yang akan dibawa ke dalam bentuk matriks. Maka, bentuknya akan seperti berikut ini:

matriks translasi transformasi geometri zenius — Matriks translasi (Arsip Zenius)

Sebelum beranjak ke pembahasan contoh soal transformasi geometri kelas 11, gue mau ngasih tahu ke Sobat Zenius, nih, kalau aplikasi Zenius bisa di-download secara gratis, lho!

Lewat aplikasi, banyak sekali fitur penunjang yang bantu elo buat belajar lebih produktif lagi. Elo bisa belajar lewat video pembelajaran, ribuan contoh soal dan pembahasannya, hingga ikutan simulasi ujian try out.

Gimana? Menarik, kan! Yuk, segera download aplikasinya dengan klik banner di bawah ini!

Download Aplikasi Zenius

Tingkatin hasil belajar lewat kumpulan video materi dan ribuan contoh soal di Zenius. Maksimalin persiapan elo sekarang juga!

Contoh Soal dan Pembahasan Matriks Translasi

Supaya lebih jelas, kita langsung masuk ke contoh soal transformasi geometri kelas 11 dan pembahasannya ya. Perhatikan soal di bawah ini!

Contoh Soal 1

Titik A(2,3) digeser sejauh T(1,2). Tentukan A’!

Jawab:

$Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 114$

Jadi, translasi titik A(2,3) adalah A’(3,5)

Contoh Soal 2

Titik A(1,3) ditransformasikan terhadap matriks $Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 115$ . Tentukan koordinat hasil transformasi titik tersebut!

Jawab:

$Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 116$

Jadi, koordinat hasil transformasi titik A adalah A’(1,9).

Matriks Refleksi

Refleksi atau pencerminan merupakan perpindahan yang sifatnya seperti cermin. Coba elo lihat ilustrasi kucing bercermin di awal tulisan ini. Nah, itu salah satu contoh dari refleksi. Atau elo coba perhatikan titik pada garis koordinat di bawah ini!

transformasi geometri refleksi dengan matriks zenius — transformasi geometri refleksi dengan matriks (Arsip Zenius)

Refleksi Terhadap Sumbu-X

Refleksi terhadap sumbu-x berarti sumbu x adalah cerminnya. Pada ilustrasi di atas, refleksi terhadap sumbu-x digambarkan oleh titik berwarna merah, yaitu A(4,3) dengan refleksinya A’(4,-3).

Jadi, yang berubah adalah y-nya, yang awalnya positif menjadi negatif, begitu pun sebaliknya.

(x,y) → (x,-y)

Kalau dibuat bentuk matriksnya, maka akan menjadi seperti ini:

$Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 117$

Refleksi Terhadap Sumbu-Y

Kalau refleksi terhadap sumbu-y, berarti yang menjadi cermin adalah sumbu-y. Pada ilustrasi di atas, refleksi terhadap sumbu-y digambarkan oleh titik berwarna biru, yaitu B(-5,5) dengan refleksinya B’(5,5).

Jadi, yang berubah adalah x-nya, yang awalnya negatif menjadi positif, begitu pun sebaliknya.

(x,y) → (-x,y)

Kalau dibuat bentuk matriksnya, maka akan menjadi seperti ini:

$Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 118$

Contoh Soal dan Pembahasan Matriks Refleksi

Supaya lebih jelas, kita langsung masuk ke contoh soal transformasi geometri kelas 11 dan pembahasannya ya. Perhatikan soal di bawah ini!

Contoh Soal 1

Tentukan bayangan titik P(1,-3) jika direfleksikan terhadap sumbu-x!

Jawab:

$Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 119$

Matriks Rotasi

Rotasi atau perputaran merupakan bentuk transformasi geometri dengan cara memutar titik sebesar θ derajat. Ada yang diputar 90°, 180°, 270°, dan θ (theta). Dengan catatan bahwa titik pusatnya adalah 0. Supaya elo makin mudah dalam memahami konsep rotasi, coba elo perhatikan ilustrasi berikut ini.

Matriks Rotasi 90°

(x,y) → (-y,x)

$Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 120$

Matriks Rotasi 180°

(x,y) → (-x,-y)

$Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 121$

Matriks Rotasi 180°

(x,y) → (y,-x)

$Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 122$

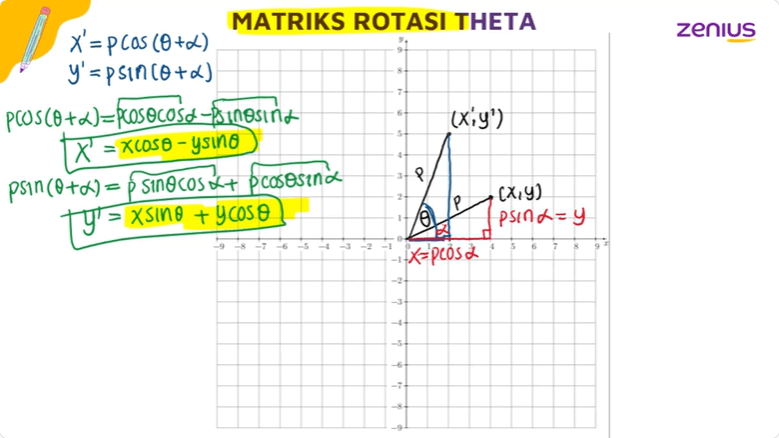
Matriks Rotasi Theta

Lalu, gimana kalau ada titik yang mau dirotasi, tapi gak diketahui derajat pastinya? Elo bisa menggunakan konsep matriks rotasi theta dengan rumus sebagai berikut.

$Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 123$

Kalau elo masih bingung mengenai rumus yang satu ini, elo bisa langsung nonton video materi Zenius tentang Matriks Rotasi Theta. Tenang, karena elo bisa mengakses videonya secara GRATIS di website atau Aplikasi Zenius. Syaratnya elo harus punya akun Zenius terlebih dahulu. Ini dia cuplikannya:

matriks rotasi theta transformasi geometri zenius — Cuplikan matriks rotasi theta transformasi geometri (Arsip Zenius)

Matriks Dilatasi

Dilatasi atau perkalian merupakan perubahan ukuran suatu titik atau objek. Pada matriks dilatasi dengan faktor skala k dan pusat 0, kita bisa ambil contoh suatu titik A(2,3), kemudian didilatasi dengan skala k=2 dan akan menghasilkan bayangan (x’y’). Maka, dapat menentukannya dengan cara di bawah ini (lihat titik warna merah).

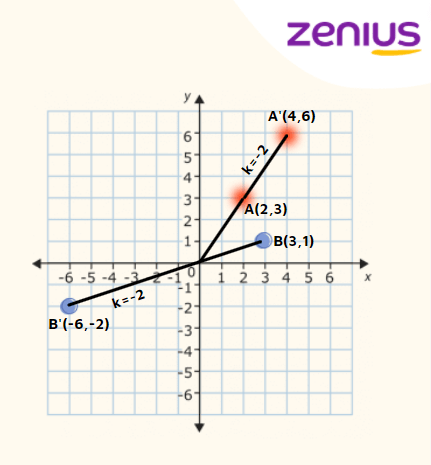
Hasil bayangan dari titik A(2,3) adalah A’(4,6). Sama aja kalau elo mau mengubah skala k-nya menjadi k=3, berarti elo tinggal kalikan titik A dengan skala k=3 menjadi A’(6,9). Sekarang gimana kalau skalanya negatif? Gampang, elo tinggal kalikan aja.

Contohnya bisa elo lihat pada gambar di atas (lihat titik warna biru). Di situ ada titik B(3,1) dengan skala k=-2, dari situ elo kalikan aja titik A dengan skala k. Hasil bayangan titik tersebut adalah B’(-6,-2).

Dari contoh ilustrasi di atas, kita bisa menuliskan rumusnya menjadi seperti ini.

(x’,y’) → (kx, ky)

$Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 124$

Lalu, bagaimana dengan matriks dilatasi dengan faktor skala k dan pusat (a,b). Coba elo perhatikan ilustrasi di bawah ini!

matriks dilatasi zenius — Matriks Dilatasi (Arsip Zenius)

Kalau sebelumnya kita menghitung dilatasi dari pusat 0, sekarang kita menghitungnya dari pusat (a,b). Sehingga, rumus yang digunakan adalah sebagai berikut:

$Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 125$

$Transformasi Geometri dengan Matriks – Materi Matematika Wajib Kelas 11 126$

*****

Demikian artikel mengenai materi transformasi geometri kelas 11 beserta contoh soal dan pembahasannya. Semoga setelah ini Sobat Zenius jadi semakin memahami materi yang satu ini, ya!

Nah, buat elo yang lebih suka belajar melalui video pembelajaran, elo bisa banget, nih, belajar melalui Zenius. Video pembelajaran dari Zenius dibawakan oleh tutor-tutor yang terpercaya sehingga materinya pun dikemas dengan baik dan menarik.

Bagi Sobat Zenius yang ingin belajar lewat video pembelajaran, khususnya mengenai materi di atas, elo bisa banget tinggal klik banner di bawah ini, ya!

Lalu, buat elo yang tertarik untuk terus mengasah otak dengan contoh soal, elo juga bisa langsung berlangganan lewat paket belajar Aktiva Sekolah dari Zenius, lho! Dengan berlangganan paket tersebut, elo bisa mengakses ribuan contoh soal dari semua mata pelajaran beserta pembahasannya.

Elo juga bisa belajar langsung bareng tutor-tutor Zenius yang berpengalaman dan bisa bantu ningkatin nilai rapor elo, makin paham materi sekolah dan bisa akses latihan soal & try out.

Bahkan, elo juga punya kemungkinan buat ikut 4x ujian try out, lho! Menarik, kan?

Klik banner di bawah ini buat berlangganan langsung, ya!