Notasi Sigma – Sifat, Cara Menghitung, dan Contoh Soalnya

Elo sering mendengar tentang sigma atau sum, kan? Nah, ternyata notasi tersebut membantu kita untuk menyederhanakan penulisan, lho! Simak selengkapnya mengenai notasi sigma di sini, yuk!

1 + 2 + 3 + 4 + 5

Perhitungan seperti di atas terbilang sangat mudah, ya, guys. Elo nggak perlu menambahkan notasi apapun, karena ngitung manual saja elo bisa. Nulis manual juga elo sanggup, karena penjumlahan di atas itu pendek dan angkanya masih sedikit, iya, kan?

Sekarang kalau pehitungannya kita naikkan.

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

Ah, masih sanggup segitu mah. Oke, gue tambah lagi menjadi penjumlahan 1-100 atau 1-1.000. Masih sanggup nulis manual seperti di atas, nggak?

1 + 2 + 3 + 4 + 5 + … + 100.

Panjang, kan, kalau elo menuliskannya secara manual dari 1 sampai 100? Nah, untuk memudahkan elo dalam menulis penjumlahan yang rumit, maka elo perlu yang namanya notasi sigma.

Namun, sebelum itu, elo perlu tahu dulu tentang induksi matematika.

Apa Itu Induksi Matematika?

Notasi sigma kelas 11 merupakan bagian dari induksi matematika. Apa yang dimaksud dengan induksi matematika? Apakah induksi yang dimaksud di sini sama dengan induksi elektromagnetik yang ada di fisika?

Beda ya, guys. Nih, gue kasih pengertian induksi matematika.

Induksi matematika merupakan salah satu metode yang digunakan untuk membuktikan suatu rumus atau formula matematika.

Namun, dalam membuktikan rumus tersebut ada syaratnya. Syaratnya adalah bahwa induksi matematika hanya bisa digunakan untuk setiap model matematika berupa persamaan atau pertidaksamaan yang variabel acaknya merupakan bilangan asli.

Elo bisa baca selengkapnya mengenai induksi matematika di artikel berikut ini.

Baca Juga: Induksi Matematika untuk Membuktikan Rumus

Selanjutnya, Apa Itu Notasi Sigma?

Setelah elo tahu bahwa induksi matematika adalah metode untuk membuktikan rumus, selanjutnya kita bahas pengertian notasi sigma, ya.

Notasi sigma merupakan sebuah lambang yang digunakan untuk mempermudah penulisan, yaitu tentang penjumlahan dari sebuah fungsi yang ada.

Lambang notasi sigma adalah “Σ”. Lambang tersebut merupakan huruf Yunani “sum” yang artinya penjumlahan.

Elo pasti sudah nggak asing dengan lambang tersebut, kan?

Kenapa, sih, kita perlu notasi ini? Kenapa kita nggak pakai saja “+” kalau untuk penjumlahan? Konsepnya sama seperti yang sudah gue jelaskan di awal. Untuk deret bilangan yang simpel, elo bisa menggunakan “+” secara langsung. Namun, untuk deret bilangan yang rumit, elo akan membutuhkan notasi ini.

Bisa dibilang, notasi sigma bertujuan untuk mempermudah penulisan. Gimana contohnya?

Oke, kita balik lagi ke deret bilangan dari 1-100. Selanjutnya, deret bilangan tersebut kita buat menjadi lebih ringkas menjadi notasi sigma, seperti ini.

Penjelasan lebih detail mengenai notasi di atas akan kita bahas di poin selanjutnya, ya.

Baca Juga: Pertanyaan yang Mungkin Tidak Kamu Pikirkan Saat Belajar Induksi Matematika

Rumus Notasi Sigma

Ketika elo menemukan deret bilangan yang rumit, elo memerlukan notasi sigma untuk mempermudah penulisannya.

Gue sudah kasih spoiler tentang rumus notasi sigma dari gambar sebelumnya. Kurang lebih rumusnya seperti ini.

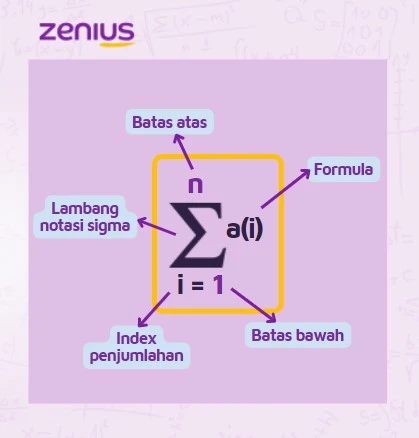
Apa itu batas atas notasi sigma, batas bawah, formula, dan indeks penjumlahan?

Batas atas notasi sigma merupakan angka terakhir yang harus dicapai dalam operasi penjumlahan. Lalu, apa itu batas bawah notasi sigma? Sebaliknya, batas bawah notasi sigma merupakan angka pertama yang harus digunakan untuk memulai operasi penjumlahan.

Formula merupakan persamaan yang harus digunakan untuk setiap indeks dari batas bawah hingga batas atasnya. Kemudian, indeks penjumlahan yaitu indeks yang akan dimasukkan sebagai variabel dalam formula.

Supaya lebih mudah dalam memahami rumus di atas, gue punya contoh soalnya, nih.

Hasil dari adalah ….

Gimana cara menghitung notasi sigma di atas? Mudah saja, elo lihat angka-angka yang terdapat pada notasi tersebut.

Diketahui:

Batas atas (n) = 5.

Batas bawah (i) = 1.

Formula = 2n.

Artinya, elo diminta untuk menentukan hasil penjumlahan dari formula 2n, dengan nilai n bergerak dari 1-5. Paham, nggak? Nih, coba elo perhatikan uraian pembahasan di bawah ini!

Untuk cara mengerjakannya, pertama elo lihat formulanya, yaitu 2n. Nah, 2n inilah yang akan elo gunakan dalam perhitungan.

Kemudian, elo masukkan 1 sampai 5 pada nilai n di formula 2n. Kenapa 1 sampai 5? Karena, batas bawah dari notasi di atas adalah 1, dan batas atasnya adalah 5. Terakhir, elo jumlahkan deh operasi perkalian dan penjumlahan di atas! Mudah, kan?

Paham ya, sampai sini?

Nah, nggak cukup sampai di situ, guys. Ada beberapa sifat notasi sigma yang perlu elo ketahui, seperti sifat perkalian seperti pada contoh di atas, sifat pangkat, dan masih banyak lagi.

Namun, elo nggak perlu bingung dan harus menghafalkan semua sifatnya, kok. Selama elo paham cara umum mengerjakan notasi sigma, gue yakin, elo pasti bisa mengerjakan semua soal dengan berbagai sifat yang ditawarkan.

Nih, gue punya referensi video materi belajar yang bisa elo gunakan untuk memahami konsep notasi sigma, supaya nggak bingung lagi kalau ditawarkan sifat-sifat yang lainnya. Klik banner di bawah ini, ya!

Contoh Soal Notasi Sigma dan Pembahasannya

Gimana, sudah paham dengan konsep yang ada di video materi belajar Zenius? Untuk menguji seberapa jauh pemahaman elo mengenai materi notasi sigma, gue punya contoh soal yang bisa elo kerjakan, nih.

Contoh Soal 1

Hasil dari adalah …..

A. 23.

B. 2.

C. -8.

D. 20.

E. 49.

Jawab: D. 20.

Pembahasan:

Diketahui:

Batas atas (n) = 5.

Batas bawah = 1.

Formula = 7 – n.

Contoh Soal 2

Hasil dari . Nilai a yang sesuai untuk melengkapi operasi di atas adalah ….

A. 3.

B. 5.

C. 7.

D. 8.

E. 9.

Jawab: B. 5.

Pembahasan:

Nggak perlu bingung, elo kerjakan saja dulu seperti biasa dengan mengabaikan nilai a atau batas atasnya. Elo perlu berhenti ketika mendekati angka 160 atau pas di angka 160.

→ (11(1) – 1) + (11(2) – 1) + (11(3) – 1) + (11(4) – 1) + (11(5) – 1) = 160.

Ternyata, setelah gue hitung sampai batas atas 5, hasil operasi penjumlahannya sesuai, guys. Artinya, niai a pada soal di atas adalah 5.

Kalau elo mau menggunakan cara manual, bisa banget, kok. Namun, memang sedikit lebih rumit. Elo bisa cek caranya pada pembahasan soal di sini.

Contoh Soal 3

Tentukan hasil dari !

Nah, coba elo kerjakan soal yang satu ini, ya! Caranya sama, kok. Bedanya hanya di formulanya. Formula pada contoh soal 3 ini menggunakan pangkat. Kalau sudah ketemu hasilnya, elo share di kolom komentar ya, supaya pembaca lainnya bisa belajar dari jawaban elo!

Baca Juga: Penjumlahan dan Pembagian Polinomial

*****

Gimana nih, sampai sini udah paham kan tentang pengertian dan rumus notasi sigma? Buat yang lebih menyukai belajar dengan nonton video, elo bisa mempelajari materi matematika lainnya di kumpulan video belajar Zenius materi Matematika Wajib.

Oh ya, Zenius punya beberapa paket belajar yang bisa lo pilih sesuai kebutuhan lo. Di sini lo nggak cuman mereview materi aja, tetapi juga ada latihan soal untuk mengukur pemahaman lo. Yuk langsung aja klik banner di bawah ini!