Artikel ini membahas tentang bagaimana cara mengukur jarak antara Matahari dan Bumi, serta benda-benda angkasa lainnya tanpa harus meninggalkan Bumi.
Halo guys! Ketemu lagi nih dengan Steve dan Wisnu. Kali ini kita berdua mau ngomongin tentang gimana caranya ngukur benda-benda angkasa. Sebelum kita mulai, lo pernah gak, sih, wondering tentang seberapa jauhnya Matahari dari Bumi? Atau jarak antara Bumi dengan Bulan? Nah, kebetulan, kita sering banget dapet pertanyaan kayak gini:
Q: Berapa sih jarak dari Bumi ke Matahari?
Z: AU lah.
Q: Eh seriusan. Kalo jarak dari Bumi ke Jupiter?
Z: AU AU AU AU AU.
Q: Apaan sih?
Z: Kan jarak dari Bumi ke Jupiter 5 kali AU.
Jadi, secara simpel, jarak antara Bumi dengan Matahari adalah 1 AU. Apa itu AU? AU adalah singkatan dari Astronomical Unit. Satuan AU ini menjadi standar jarak semua benda angkasa yang terletak di dalam Tata Surya.
Berhubung saat ini yang kita ketahui kehidupan dan peradaban yang berkembang hanya berada di Bumi, kita menjadikan jarak antara Bumi ke Matahari menjadi standar. Sedangkan Matahari dijadikan acuan simply karena semua benda langit yang ada di tata surya mengelilingi Matahari. Bahkan, jika kita sudah punya koloni di Mars atau di planet lain, menurut gue AU tetep akan jadi ukuran jarak standar. Home planet kita tetep aja Bumi.
Gue nggak bisa nekenin lagi seberapa pentingnya jarak antara Bumi ke Matahari untuk bisa mengukur seberapa besarnya tata surya.
Nah, di sini gue pengen ngebahas, nih, gimana ceritanya manusia bisa sampai pada standar 1 AU yang kita pakai sekarang ini. Gini ceritanya.
Metode Aristarchus
Elo bakalan kaget, gak? kalo gue bilang bahwa perjalanan manusia mengukur jarak antara bumi dan matahari dimulai sekitar 250 tahun sebelum masehi? That is the truth! Aristarchus (310-230 SM) tercatat dalam sejarah sebagai manusia pertama yang mencoba mengukur jarak matahari dari bumi.
Teori-teori yang disampaikan Aristarchus ini keren banget, mengingat beliau ada pada saat ilmu pengetahuan masih baru banget berkembang. Dari karya-karya beliau yang masih bisa dibaca, Aristarchus memprediksi bahwa pusat dari tata surya adalah Matahari. Tentu teori beliau masih sekitar 1800 tahun terlalu dini sampai dikorek oleh Nicholas Copernicus hingga menjadi sebuah teori astronomi yang paten. Tapi, karya beliau yang paling dikenal adalah perhitungan jarak antara Matahari dari Bumi.
Sebelum kita mulai mengupas persamaan yang dirangkai Aristarchus, lo harus paham dulu bahwa jarak Matahari dari Bumi berubah setiap detiknya. Iya karena rotasi dan revolusi Bumi. 1 AU yang kita liat diatas itu merupakan jarak rata-rata dihitung dari orbit terjauh Bumi dari Matahari (Aphelion) dan orbit terdekat Bumi dari Matahari (Perihelion).
Aristarchus ini adalah salah satu astronom di zaman Yunani kuno. Dia lahir tahun 320 Sebelum Masehi. Bisa bayangin itu setua apa? Sekitar 2200 tahun sebelum Indonesia merdeka, 1600 tahun sebelum Majapahit, dan 700 tahun sebelum kerajaan Kutai (kerjaan pertama di Nusantara). Pada zaman itu, tentu ga ada yang bisa bikin roket ke luar angkasa untuk mengukur jarak dari matahari ke bumi. Terus gimana cara Aristarchus ini bisa mengukur jaraknya?
Okay, sebenernya Aristarchus ini belum benar-benar mengukur jarak dari matahari ke bumi. Yang dia lakukan itu cuma mengukur perbandingan antara jarak bumi-matahari dan bumi-bulan. Dia melakukan pengukuran ini ketika bulan tampak setengah lingkaran dari bumi. Wah, gimana caranya tuh?
Nah, sebelum lu scroll ke bawah, coba pikir dulu, kira-kira gimana metode dia untuk mengukur perbandingan jarak Bumi-Matahari dan Bumi-Bulan ketika bulan tampak setengah lingkaran. Petunjuknya: Gambar posisi Bulan, Matahari, dan Bumi ketika bulan tampak setengah lingkaran. Contohnya seperti gambar Bulan berikut ini. ?
Okay, gue lanjutin ya.
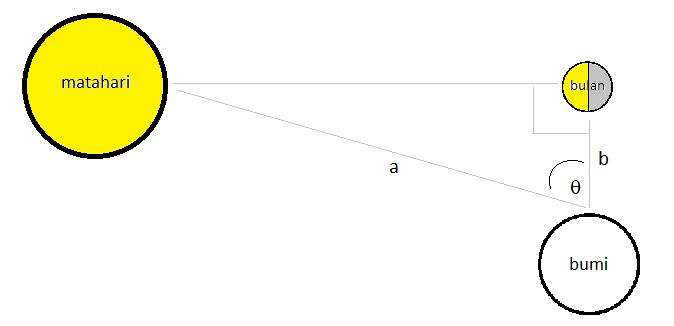
Ketika bulan tampak setengah lingkaran dari permukaan bumi, maka matahari, bulan, dan bumi akan membentuk sudut tegak lurus seperti gambar berikut ini:
Okay, perlu gue tekankan bahwa gambar di atas itu simplifikasi dari posisi sebenarnya,ya. Harusnya matahari itu jauh lebih besar dari pada bumi dan bulan, sudut θ juga harusnya ga setajam itu, tapi mendekati 90 derajat. Tapi penggambaran ini ga jauh beda dengan apa yang dilakukan oleh Aristarchus.
Nah, untuk bisa mendapatkan perbandingan antara b dengan a, kira-kira apa yang harus dilakukan oleh Aristarchus? Dia tinggal menghitung sudut θ!
Menghitung sudut bulan-bumi-matahari (sudut θ)
Teknik yang dilakukan oleh Aristarchus untuk menghitung sudut θ ini ga jauh berbeda dengan yang dilakukan oleh Eratosthenes.
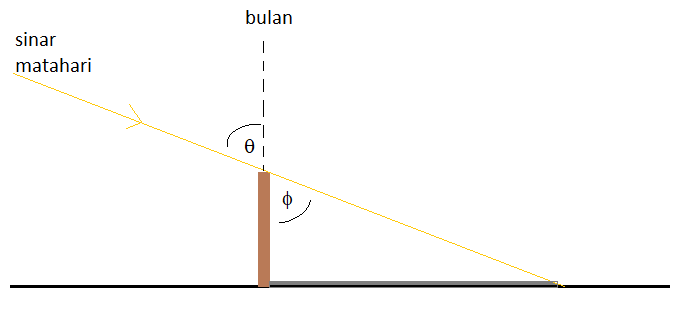
Aristarchus tinggal meletakkan sebuah tongkat secara tegak ketika bulan itu berada tepat di atasnya, seperti gambar di atas. Berikutnya, dia bisa mengukur bayangan yang terbentuk akibat adanya sinar matahari di atas. Sudut ɸ bisa dicari dengan persamaan:
tan ɸ = Panjang bayangan / Panjang tongkat
Berhubung sudut ɸ dan sudut θ saling bertolak belakang, maka kita bisa menyimpulkan bahwa:
θ = ɸ
Hore! Aristarchus berhasil menghitung sudut antara bulan-bumi-matahari!
Perbandingan jarak bumi-bulan dengan bumi-matahari
Setelah sudut θ diketahui, perbandingan antara b dengan a pada gambar di atas tentu gampang dicari dong, ya? Yup, langsung aja:
Cos θ = b/a
Nah, Aristarchus melakukan hal di atas dan menemukan bahwa sudut θ itu besarnya adalah 87o. Tinggal kita masukkan ke persamaan, deh:
Cos 87o = 1/19
Wah, berarti dapet nih! Perbandingan jarak bumi-bulan dengan bumi-matahari adalah 1:19! Aristarchus pun senang. ?
Eh tunggu! Kok udah pakai Trigonometri sih? Emangnya di zaman Yunani kuno, Trigonometri sudah ditemukan?
Okay, tentu Trigonometri yang kita kenal sekarang dengan nama-nama yang sok asik itu (sin, cos, tan) belum dikenal. Tapi konsep perbandingan segitiga siku-siku itu udah dikenal pada zaman Yunani kuno. Jadi ketika Aristarchus itu menemukan bahwa sudut yang harus dia cari perbandingannya adalah 87o misalnya, dia tinggal menggambar suatu segitiga siku-siku yang salah satu sudutnya adalah 87o. Setelah itu, dia ukur perbandingan antara sisi samping dengan sisi miringnya. Jadi dia ga perlu tahu tentang cosinus untuk bisa melakukan hal ini karena Trigonometri pun konsep dasarnya adalah dari perbandingan segitiga.
Perhitungannya Aristarchus ini akurat ga sih?
Meskipun metodenya Aristarchus ini menarik, tapi sayangnya hasil perhitungan dia sangat jauh dari ukuran yang sebenarnya. Menurut perhitungan modern, sudut sebenarnya itu bukan 87o, tapi 89,83o. Kalau kita masukkan ke dalam cosinus, hasil perhitungannya adalah 1:400. Jauh banget ya.
Supaya dia nggak sedih, gimana kalau kita bilang ke Aristarchus, “Ga apa-apa kok, Aristarchus! Aku tetap bangga sama kamu!”
Anyway, meskipun belum akurat, tapi belum ada yang berhasil mengoreksi perhitungan Aristarchus ini sampai 1900 tahun kemudian loh! Sudut pengukuran Aristarchus ini kemudian diperbaiki oleh Godefroy Wendelin.
Temuan Wendelin & Horrocks
Pada abad ke-17, seorang astronom dari Flandria (sekarang merupakan bagian dari Belgia) bernama Godefroy Wendolin menggunakan teleskop untuk mengoreksi observasi sudut yang terbentuk diantara Bulan-Bumi-Matahari. Dengan kata lain, paman Wendolin mengoreksi metode Aristarchus. Ia juga memetakan lokasi bintang yang tersebar di angkasa.
Beliau mengamati bahwa besar sudut tersebut bukanlah 87o namun 89,7o-89,75 o. Dengan koreksi tersebut maka kita dapat mengubah persamaan kita diatas tadi dan mendapatkan bahwa perbandingan jarak antara Bumi ke Bulan dan Bumi ke Matahari sebenernya mencapai 1 berbanding 220.
Wow. Sekarang kita udah deket banget dengan nilai perbandingan jarak yang sebenarnya yaitu sekitar 1 berbanding 400.
Selang 4 tahun kemudian, Jeremiah Horrocks (seorang astronom dari Inggris) menemukan metode lain untuk mengukur jarak antara Bumi dan Matahari. Untuk mengukur jarak tersebut beliau menggunakan posisi relatif Venus terhadap Matahari. Perhitungan Horrocks dilakukan dengan pengamatan terhadap Venus dari berbagai tempat di Bumi.
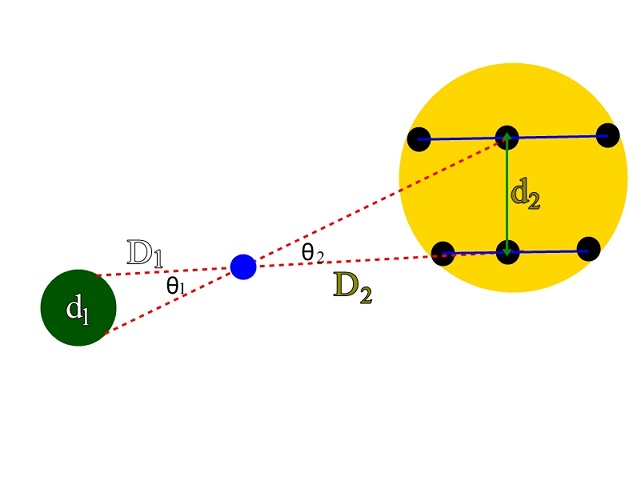
Untuk memahami metode Horrocks, kita coba buat datanya lebih simpel dengan menaruh pengamatan pada dua titik saja. Coba perhatikan ilustrasinya.
Nah, dari kedua lokasi tersebut, dilakukan pengamatan terhadap posisi Venus ketika posisi orbitnya dapat diamati dari Bumi. Posisi Venus ketika mengorbit Mataharinya pun diamati tidak hanya sekali saja. Kemudian Horrocs dapat memperhitungkan secara kasar berapa jarak d2 dengan menggunakan geometri.
Dengan menggunakan hubungan sudut, diketahui bahwa θ1 dan θ2 besarnya sama. Kemudian dengan menggunakan nilai sin untuk sudut yang sangat kecil, diperoleh bahwa perbandingan d1/D1 sama dengan d2/D2. Dengan ilustrasi tersebut Horrocks juga dapat memperoleh estimasi jarak antara Bumi ke Matahari yaitu sekitar 144,840,960 km. Perhitungan beliau meleset sekitar 10 juta kilometer tapi nilai ini udah bagus banget.
Metode Parallax

Metode berikutnya adalah sebuah metode yang dinamakan Metode Parallax. Metode ini digunakan oleh seorang yang bernama Giovanni Cassini. Ia menjadi orang pertama yang bisa memberikan nilai yang cukup akurat mengenai jarak antara Matahari ke Bumi. Bagaimana Cassini bisa mendapatkan angka tersebut? Dengan mengukur jarak antara Bumi dan Mars. Loh? Iya, doi ngukur jarak antara Bumi dan Mars dulu, abis itu baru dia ngukur jarak antara Bumi dan Matahari.
Gini ceritanya. Pada tahun 1672, Cassini menggunakan sebuah alat yang biasanya digunakan oleh pelaut untuk navigasi. Kecuali elo bajak laut atau pelaut mungkin elo nggak akan familiar dengan alat ini. Nama alatnya itu sextant. Ini aksesoris yang ditempel pada teleskop. Bentuknya kayak gini.

Bentuknya mirip busur, ya? Nah, alat yang di bawahnya ini bisa ngukur nilai sudut yang cukup akurat. Jauh lebih akurat daripada ngukur sudut pake tongkat atau teleskop. BTW, sebenernya metode yang digunakan oleh Cassini ini sempat terlebih dahulu digunakan oleh seseorang bernama Huygens. Akan tetapi, banyak asumsi yang digunakan Huygens meleset sehingga Huygens dinyatakan tidak ilmiah. Maka Cassini dinyatakan sebagai penggagas metode yang biasa disebut sebagai Parallax.
Nama mereka digunakan untuk dijadikan satelit yang digunakan untuk mempelajari Saturnus. Cassini-Huygens nama satelit buatannya, namun lebih dikenal dengan sebutan satelit Cassini. Kasian deh Huygens, nggak saintifik sih lo. Satelit ini merupakan satelin pertama yang berhasil memasuki orbit Saturnus.

Eksperimen untuk Mencari Sudut Parallax
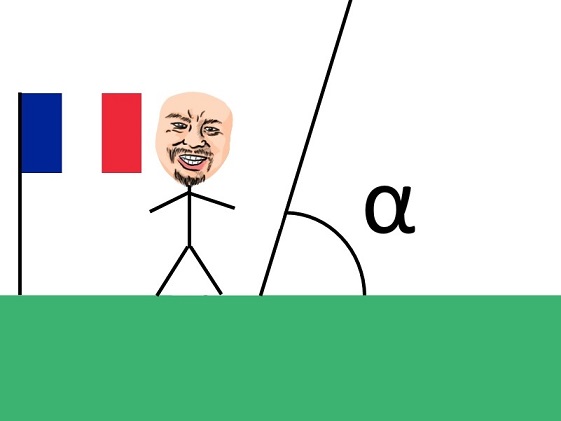
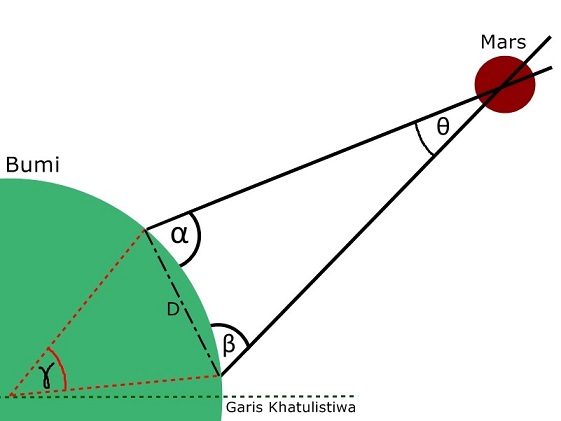
Sekarang kita bakal ngomongin bagian serunya nih. Huehehhe. Ekseperimen ini dilakukan Cassini dengan mengukur sudut yang terbentuk antara Mars dan Bumi dari dua sudut pandang berbeda. Nah yang gue jelasin di sini itu versi sederhana dari eksperimennya yah. Kalo aslinya, Cassini ngumpulin data segambreng dulu. Jadi dapat hasil rata-ratanya. Cassini melakukan pengukuran dari 2 tempat, yaitu Perancis dan Guyana Perancis (French Guyana).
Di Paris, Perancis, Cassini mendapatkan sudut alpha sebagai berikut:
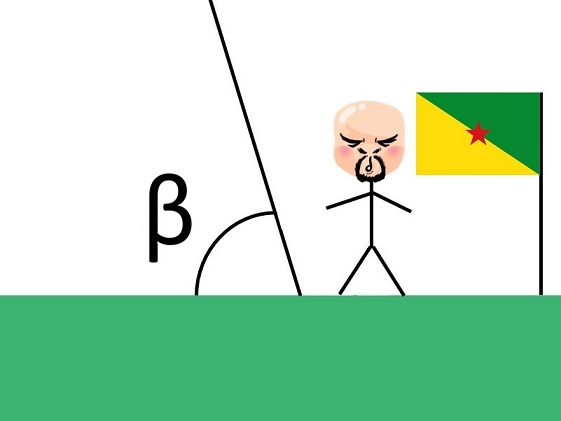
Kemudian Cassini mengirim seorang kolega bernama John Richer untuk mengukur di Guyana Perancis. Guyana Perancis ini lokasinya ada di Amerika Selatan, ya. Kemudian, Richer mendapatkan sudut beta sebagai berikut:
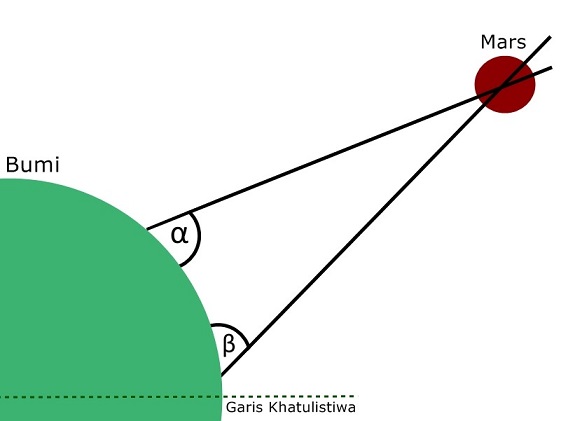
Begitulah wajah Richer yang bete, soalnya harus keluar dari zona nyaman di Eropa dan menjelajah Amerika Selatan dulu untuk memperoleh data. Anyway, kalau kedua gambar itu kita zoom out, maka sudut alpha dan beta itu menjadi seperti ini:
Berhubung mereka bisa mengetahui posisi Paris dan Guyana Perancis dengan menghitung sudut ke matahari, maka mereka bisa tahu sudut gamma di bawah ini:
Nah, sudut Parallax yang mau mereka cari itu adalah sudut theta di bawah ini:
Sekarang elo gue kasih puzzle, nih (biar kesannya bukan soal) biar lebih rame dan seru. Kalau alpha, beta, gamma sudah diketahui, gimana cara mencari sudut thetanya? Nih biar kebayang gue kasih angka (ini bukan nilai sebenarnya yah):
Misalkan besar sudut α = 75o. Terus sudut β besarnya 70o. Besar sudut γ itu 25o. Berapa coba nilai sudut θ (Parallax-nya )? Silakan jawab di kolom komentar, ya.
Kalo elo bingung gimana nyelesaiin puzzle-nya, nih gue kasih clue.
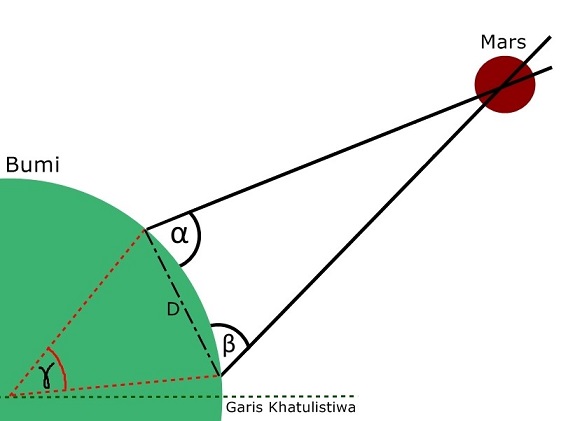
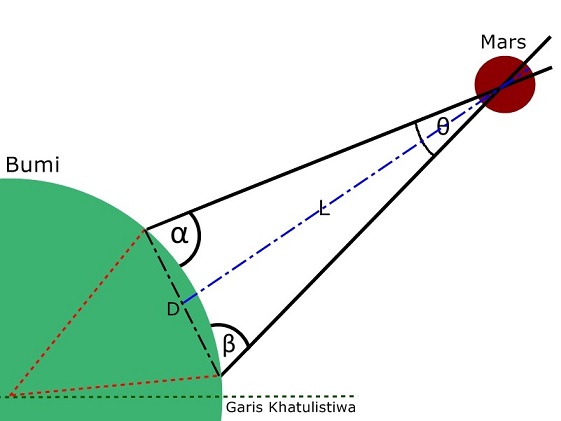
Jarak Bumi-Mars
Nah, kalau sudut parallax sudah diketahui, gimana cara Cassini menghitung jarak dari Bumi ke Mars? Kita gambar lagi yah.
Puzzle terakhir nih terakhir. Tapi elo bakal paham, nih gimana cara ngitung jarak ke Mars.
Misalkan D itu besarnya 7.000 km. Kemudian misalkan sudut parallaxnya adalah 10o. Berapakah nilai L? (tulis jawaban lu di comment lagi ya)
Sekali lagi kalo elo bingung, lo bisa cek artikel yang gue kasih tadi.
Seru kan? Iseng-iseng berhadiah ilmu pengetahuan *tsaaah. Sekali lagi gue ingatkan nilai yang gue kasih di puzzle tadi, tuh, bukan nilai sebenarnya, yah. Sudut parallax itu aslinya nilainya nol koma sekian derajat. Kecil banget nilainya. Jadi nanti nilai L yang didapet yah gede banget juga, men.
Jarak Bumi-Matahari
Cassini sudah bisa menghitung jarak Bumi-Mars, tapi kan yang mau kita cari adalah jarak Bumi-Matahari. Jeng jeng. Ternyata belum selesai yah. Kebetulan, Astronom sebelum Cassini sudah bisa mengetahui jarak Mars ke Matahari (ini ga kita bahas di sini ya karena kepanjangan). Kemudian, Cassini juga bisa mengukur sudut Mars-Bumi-Matahari, sebut aja sudut θ. Hati-hati ketuker dengan θ yang sudut parallax tadi yah. Kalau kita gambarkan ketika benda langit tersebut, gambarnya jadi begini:
Okay, kalau kita tahu besar L, x, dan theta, gimana cara menghitung p? Nih gue kasih angkanya lagi:
Diketahui nilai dari x adalah 228 km dan nilai dari L adalah 55 km. Sudut θ diketahui sebesar 60o Berapakah nilai p? (tulis jawaban di komentar di bawah ya)
Clue-nya juga ada di artikel tadi, ya.
Bagaimana dengan Perhitungan di Era Modern?
Meski nilai yang diperoleh oleh Cassini memang tidak seratus persen akurat, yaitu meleset sekitar 6% dari nilai yang kita dapat dari hasil eksperimen di abad 21. Namun, untuk tepat dugaan lo. Nilai yang kita punya masih merupakan hasil suatu perhitungan dan mungkin saja dalam beberapa waktu ke depan seiring dengan berkembangnya ilmu pengetahuan, akan terjadi koreksi lagi terhadap nilai AU.
Di era modern ini, jika kita ingin melakukan perhitungan jarak antara Bumi dan benda langit lainyya, kita bisa memanfaatkan teknologi seperti satelit. Pengukuran dilakukan dengan mengirimkan satelit mendekati benda langit yang ingin kita ukur jaraknya. Setelah itu yang perlu kita lakukan adalah mengirimkan sinyal pada satelit tersebut dan menunggu waktu terpantulnya sinyal tersebut oleh satelit sampai kembali ke Bumi.
Keren, yah. Ternyata pertanyaan-pertanyaan yang mungkin tidak pernah terbayangkan untuk bisa dijawab oleh manusia dapat dicari jawabannya dengan metode yang simpel. Dengan geometri yang cukup sederhana dan pengetahuan untuk mengukur sudut, kita dapat mengukur berbagai hal seperti jarak dan diameter dari beragam benda langit yang ada di alam semesta.
So, jangan pernah sekalipun menggantung mimpimu hanya setinggi pohon mangga, apalagi pohon toge. Gantungkan mimpimu setinggi langit. Bahkan Matahari yang belum mencapai ujung langit saja berjarak 149.597.870.700 meter dari Bumi yang kita pijak. Siapa tahu dalam 30 tahun kedepan elo akan menjadi orang Mars pertama? Berarti elo menggantungkan cita-cita lo setinggi 229 juta kilometer.
Anyway, sekian dulu pembahasan dari kami. Semoga tulisan ini bisa menginspirasi lo untuk terus menggali ilmu tentang alam semesta. To quote Buzz Lightyear, to infinity and beyond!











wihh.. mantap artikelnya !!! request dong buat artikel cara mengetahui isi bumi (Kandungannya), beserta panas inti bumi.
Request ditampung yah!
request dong kak buat artikel tentang gimana proses yang akan terjadi jika meteor jatuh ke bumi?
Meteor banget nih? Ditampung dulu yah requestnya. Haha.
Kak gw udh nyoba itung, nah yg sudut paralaks gw dapetnya 5 derajat, kalo yg jarak L 59.5K km, kalo yg p dapetnya 280.55…. km, nanti gw cb upload caranya,susah banget ngupload gambar di hp ini 🙁
https://ibb.co/jRU4Fy
Nah ini yg nomer 1 sama 2
https://ibb.co/dqai8J
Kalo yg ini nomer 3
Maaf kalo tulisannya jelek wkwkw
Coba yang laen kerjain tanpa ngelihat cara yang di upload disini. Ada yang dapet jawaban yang beda nggak?
Kalo udah pada ngerjain baru deh bandingin perbedaan caranya dimana.
Btw terimakasih inisiatifnya untuk langsung mengerjakan ‘teka-teki’ di artikel yah!
Gw no1 dapetnya 10 kak
Wiih. Coba lo jelasin gimana caranya bisa dapet 10. Gausah malu2. Haha.
https://uploads.disquscdn.com/images/9ab6398c5ed249d00d27665eb67fab71f741528c390c522573a53ad4d67574d9.jpg
Berikut solusi dari gue untuk pertanyaan nomor 3: “Diketahui nilai dari x adalah 228 km dan nilai dari L adalah 55 km. Sudut θ diketahui sebesar 60^o. Berapakah nilai p?”
https://uploads.disquscdn.com/images/0b994950e6fafe6dd666a5d0ac404ce2ae21dc071ddc048f0be2eba0a9914ba7.jpg https://uploads.disquscdn.com/images/75fa7a2980af5473870eb318516dfa60984ebc95811fbbd9e5e4a0401d664339.jpg
Kak aku agak bingung sama yg no.3
Itu pake konsep yang mana ya?
Solusi di atas menggunakan konsep aturan Kosinus. Lu bisa review teori dan latihan soal di sini: https://www.zenius.net/lp/c6600/aturan-kosinus-latihan-soal .
request artikel tentang “filsafat dan hubungan dengan atheis dong” !!,
Gw no1 jwbnya 10
https://uploads.disquscdn.com/images/9ab6398c5ed249d00d27665eb67fab71f741528c390c522573a53ad4d67574d9.jpg
No3 jwbnya 141.5 https://uploads.disquscdn.com/images/f63fd40cf8d2667945f83e9980c66ed59d310bdffd0761a1a2403c502682aa1e.jpg
No2 menurut saya perlu diketahui apakah garis L nya tegak lurus D atau membelah D jadi 2 atau membelah tetha menjadi 2
Hmm.. Tolong dicek perasaan gue aja apa emang nih video belom kelar.
Home SMA SBMPTN SBMPTN – Paket Ujian TKPA SBMPTN – TPA (Tes Potensi Akademik) Basic Thinking and Reasoning Skills BAB 4A – Deductive Reasoning and Logic – Teori
Kode Konten : 2033
Soal no 20
Hmm.. Gue nemu lagi nih ,tolong dicek
Home SMA SBMPTN SBMPTN – Paket Ujian TKPA SBMPTN – TPA (Tes Potensi Akademik) Basic Thinking and Reasoning Skills BAB 5 – Deductive Reasoning and Logic – Soal Analitik
Kode Konten : 203
Kode Modul : XPTPA0402
Dari soal no 2-11.
Mulai dari gambar soalnya yg harusnya soal no 3 malah jadi 2, soal no 4 malah jadi no 3 dan seterusnya, walaupun udah gue reload atau refresh mulai dari tab atau gambarnya tapi tetep aja gk berubah.
Trus lagi dipembahasan soal no 4 kayaknya ada yg salah, bukan hasilnya tapi entah itu ketikan soalnya atau tutornya yg salah baca hurufnya.
No1nya Gimana sih Kasih tau dong? nih hasil no 2 dan da 3 saya. https://uploads.disquscdn.com/images/8f8cc6db1713ba84f98c1fe95800c6932a2f2344e473b79b2cddfb2bc63cccad.jpg https://uploads.disquscdn.com/images/cdf642e0eaad0be285102a3b13d43419ffd016ef886b24677ee0dd4f0efb1021.jpg
Kak req donk.
Bikinin artikel ttg knpa sperma x sel telur itu bisa jadi manusia ?
Kalo cuman protein, kan di daging juga bnyk protein, knp gk di pacarkan aja daging kurban yg udh di potong, siapa tau bisa jadi kambing lagi :v
Terus kan katanya ad teori ttg organisme pertama dulu ad karena asam amino yg di tembak ama petir gede. Nah di dalam perut ibu ada petir Segede itu kah ?
Intinya req ya kak ttg sperma x sel telur -> jadi bayi.
Thanks
Halo zen, nice to read this article, emang sih zen kalo bikin artikel bisa membawa pembaca untuk berpikir dan isi artikel yang dikemas dengan ringan :), tapi gue mau nanya niih kasih tips dong gimana cara kita mencari artikel atau sumber bacaan seperti ini di media yang lain, I mean kayak gimana cara author blog zenius bisa dapetin insight itu dan bisa dikonversi jadi konten artikel kayak gini,
Keren kak artikelnya. Btw, cata cassini dapet sudut theta antara mars dan matahari caranya gimana yah kak?
Jurusannnn Teknologi Pangan Berbasis Halal? Jurusan Paling Dicari? Ayo Mampir Kesini https://wp.me/pa6NeQ-a
kak untuk theta dalam menghitung L itu dibagi 2 atau gimana ya? kalo iya berarti 10 derajat dibagi 2 kah? maaf masih kurang paham kak
Min kenapa parallax nya engga langsung ke matahari?