Persamaan Linear Dua Variabel: Metode Eliminasi & Substitusi

Hai Sobat Zenius! Balik lagi nih sama materi matematika. Pada artikel kali ini kita akan bahas contoh soal dan materi sistem persamaan linear dua variabel (SPLDV) metode eliminasi dan substitusi. 

Materi sistem persamaan linear dua variabel ini udah sering muncul  di pelajaran SMA, mungkin elo udah nggak asing lagi. Apa sih SPLDV? Fungsinya apa? Cara hitungnya gimana? 

Nah mending langsung kita simak aja yuk materi dan contoh soal persamaan linear dua variabel di artikel ini.

Definisi Sistem Persamaan Linear Dua Variabel (SPLDV)

Sistem persamaan linear dua variabel atau dalam matematika biasa disingkat SPLDV adalah suatu persamaan matematika yang terdiri atas dua persamaan linear (PLDV), yang masing-masing bervariabel dua, misalnya variabel x dan variabel y.

Ciri-Ciri SPLDV:

• Sudah jelas terdiri dari 2 variabel
• Kedua variabel pada SPLDV hanya memiliki derajat satu atau berpangkat satu
• Menggunakan relasi tanda sama dengan (=)
• Tidak terdapat perkalian variabel dalam setiap persamaannya

SPLDV juga ada fungsinya loh dalam menyelesaikan kejadian di kehidupan kita. Seperti menghitung keuntungan atau laba, mencari harga dasar atau harga pokok suatu barang, dan membandingkan harga barang.

Nah, sebelum masuk ke rumus dan metode, kita tentunya harus paham unsur-unsur yang ada pada sistem persamaan linear 2 variabel. Apa aja sih?

• Variabel, yaitu pengubah atau pengganti suatu bilangan yang belum diketahui nilainya secara jelas. Variabel biasanya disimbolkan dengan huruf, seperti a, b, c, … x, y, z. Misalnya jika ada suatu bilangan yang dikalikan 2 kemudian dikurangi 9 dan hasilnya 3, maka bentuk persamaannya adalah 2x – 9 = 3. Nah x merupakan variabel pada persamaan tersebut.
• Koefisien, yaitu bilangan yang menjelaskan banyaknya jumlah variabel yang sejenis. Koefisien terletak di depan variabel. Misalnya ada 2 buah pensil dan 4 buah spidol, jika ditulis dalam persamaan adalah 

Pensil = x , spidol = y

Jadi persamaannya adalah 2x + 5y. Nah karena x dan y adalah variabel, maka angka 2 dan 5 adalah koefisien.

• Konstanta, yaitu nilai bilangan yang konstan karena tidak diikuti oleh variabel di belakangnya. Misal persamaan 2x + 5y + 7. Konstanta dari persamaan tersebut adalah 7, karena tidak ada variabel apapun yang mengikuti 7.
• Suku, yaitu bagian-bagian dari suatu bentuk persamaan yang terdiri dari koefisien, variabel, dan konstanta. Misal ada persamaan 7x -y + 4, maka suku suku dari persamaan tersebut adalah  6x , -y , dan 4.

Sebelum lanjut belajar tentang rumus sistem persamaan linear dua variabel, subtitusi dan eliminasi, yuk didownload dulu aplikasi Zenius di gadget elo. Matematika bisa jadi menyenangkan dan mudah dimengerti bareng ZenBot dan ZenCore. Tonton juga video belajar gratisnya dengan klik banner di bawah ini!

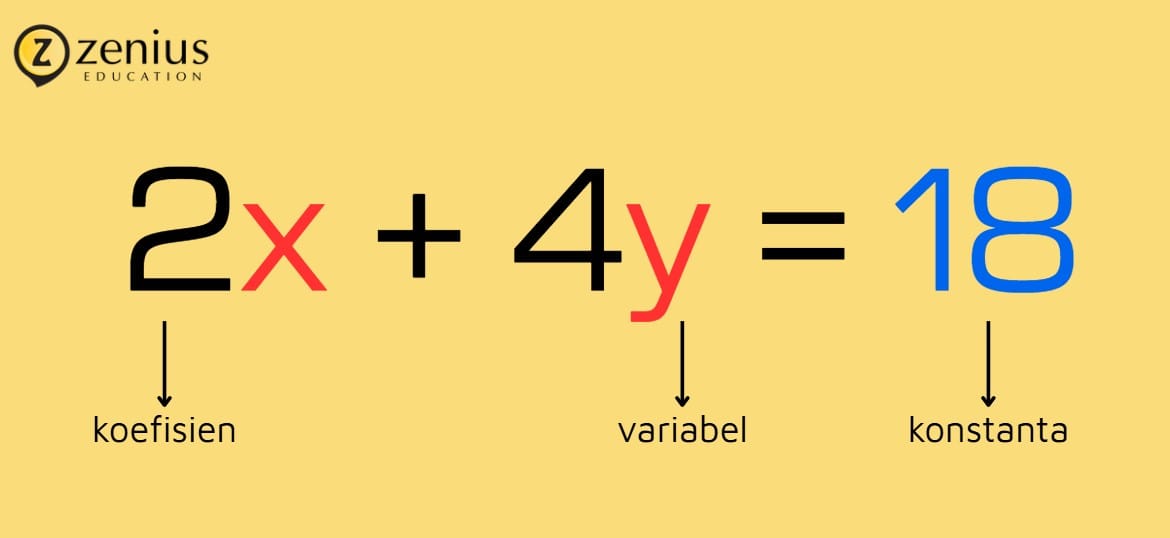
Rumus Persamaan Linear Dua Variabel

Kalau elo udah paham unsur-unsur di atas, elo mungkin sudah bisa menyimpulkan rumus linear dua variabel. Rumusnya adalah sebagai berikut:

ax + by = c

Tapi apakah cukup dengan menghapal rumusnya saja? Tentu tidak ya. Dari rumus ini setidaknya elo sudah bisa tahu materi matematika apa yang akan elo kerjakan.

Bakal penting banget nih buat elo yang sedang bersiap menghadapi UTBK. Nah, untuk cara menghitung sistem persamaan linear dua variabel bisa elo baca di bawah ini.

Metode Penyelesaian Sistem Persamaan Linear Dua Variabel

Terdapat beberapa cara atau metode dalam menyelesaikan soal persamaan linear dua variabel. Metode tersebut adalah subtitusi dan eliminasi.

Pahami kedua metode ini lewat contoh soal SPLDV metode eliminasi dan substitusi yang akan dibahas setelah ini,

Metode Substitusi

Metode substitusi merupakan salah satu cara menyelesaikan SPLDV dengan cara mengubah satu variabel dengan variabel dari persamaan lain. 

Langsung cek contoh soal SPLDV metode substitusi di bawah ini ya.

Contoh Soal Metode Substitusi

Tentukan nilai variabel x dan y dari kedua persamaan berikut dengan menggunakan metode substitusi matematika!

2x + 4y = 28 

3x + 2y = 22

Jawab:

Pertama, elo harus pilih salah satu persamaan yang akan dipindahkan elemennya. Misalnya pilih persamaan pertama yaitu

2x + 4y = 28

Lalu pilih variabel y untuk dipindahkan ke ruas kanan. Maka, persamaannya berubah jadi

2x = 28 – 4y

Karena tadi elo memilih variabel y yang dipindah, maka koefisien pada variabel x dihilangkan dengan cara membagi masing-masing ruas dengan nilai koefisien x.

2x/2 = 28-4y/2

Maka dihasilkan persamaan x = 14 – 2y sebagai bentuk solusi dari variabel x.

Setelah itu, gabungkan persamaan 3x + 2y = 22 (yang tadi tidak pilih pada soal) dengan persamaan x = 14 – 2y dengan cara mengganti variabel x dengan persamaan

x = 14 – 2y

3x+ 2y = 22

3 (14 – 2y) + 2y = 22     (Di bagian ini variabel x sudah diganti dengan x= 14 -2y, ya)

     42 – 6y  + 2y = 22

                    -4y = 22 – 42

                    -4y = -20

                -4y/-4 = -20/-4

y = 5.

Maka, ditemukan variabel y adalah 5. 

Setelah ditemukan variabel y = 5, sekarang tinggal cari x dengan memasukkan 5 sebagai variabel y.

x = 14 – 2y

x = 14 – 2(5) 

x = 14 – 10

x = 4. 

Maka ditemukan variabel x adalah 4.

Sehingga jawaban dari soal SPLDV di atas adalah x = 4 dan y = 5.

Metode Eliminasi

Penyelesaian SPLDV menggunakan metode eliminasi adalah dengan menghapus atau menghilangkan salah satu variabel dalam persamaan tersebut. Misal, variabel dalam persamaan adalah a dan b, nah untuk mencari nilai a, kita harus menghilangkan b terlebih dahulu, begitu juga sebaliknya.

Biar makin paham langsung kerjain contoh soal SPLDV metode eliminasi aja yuk!

Contoh Soal Metode Eliminasi

Tentukan nilai variabel x dan y dari persamaan berikut

x + 2y = 20

2x + 3y = 33

Dengan menggunakan metode eliminasi!

Jawab:

Pertama, cari nilai variabel x dengan cara menghilangkan y pada masing-masing persamaan.

x + 2y = 20

2x + 3y = 33

Koefisien pada variabel y dari masing-masing persamaan tersebut adalah 2 dan 3.

Selanjutnya kita cari KPK (kelipatan persekutuan terkecil) dari 2 dan 3.

2 = 2, 4, 6, 8, …

3 = 3, 6, 8, …

Setelah tahu KPK dari 2 dan 3 adalah 6, kita bagi 6 dengan masing masing koefisien.

6 : 2 = 3 → x3

6 : 3 = 2 → x2

Kemudian, kalikan dan lakukan eliminasi dengan menggunakan hasil pembagian masing-masing tadi

x + 2y = 20       | x3

2x + 3y = 33 _   | x2

Maka menghasilkan:

3x + 6y = 60

4x + 6y = 66 _

-x          = -6

 x          =   6

Sehingga dapat diketahui bahwa nilai x = 6. Untuk mencari variabel y, elo juga bisa menggunakan cara yang sama, hanya dibalik saja.

Itu tadi contoh soal eliminasi 2 variabel. Udah paham belum nih? Yuk cek pemahaman elo udah sampai mana dengan kerjain contoh soal SPLDV berikut ini!

Contoh Soal Persamaan Linear Dua Variabel

Pembahasan sebelumnya gue udah ajak elo menghitung dengan metode subtitusi dan eliminasi. Yang kali ini gue juga mau ngasih tau bentuk soal pilihan ganda SPLDV yang mungkin keluar di TPS nanti.

Di bawah ini yang merupakan sistem persamaan dua variabel adalah …

a. 2x + 4y + 4xy = 0

b. 2x + 4y = 14

c. 2x + 4 = 14

Dari pilihan a, b dan c mana nih yang termasuk dalam SPLDV? Gini nih cara jawabnya, elo tinggal lihat rumus SPLDV yang tadi udah dibahas.

Yup, jawabannya adalah pilihan b. Coba elo perhatikan pilihan b memiliki 2 variabel yaitu x dan y. Sedangkan, pilihan a memiliki 3 variabel yaitu x, y dan xy. Apalagi pilihan c yang hanya memiliki satu variabel yaitu x.

Jadi,  sistem persamaan yang merupakan sistem persamaan linear dua variabel adalah 2x + 4y = 14.

Nah, jadi sekian penjelasan singkat tentang sistem persamaan linear dua variabel (SPLDV), PLDV, serta cara-cara penyelesaiannya. Jangan lupa sering-sering latihan ya biar makin paham!

Belajar materi ini lagi yuk bareng penjelasan oleh Zen Tutor, cukup klik banner di bawah ini dan jadi lebih banyak tau!

Cobain yuk pengalaman belajar yang menyenangkan dan mudah dimengerti di live class Zenius. Dapatkan pula tryout ujian sekolah dan ribuan video materi pembelajaran dengan membeli paket belajar Zenius. Tingkatin prestasi bareng Zenius, langganan sekarang!

Baca Juga Artikel Matematika Lainnya

Determinan Matriks dan Cara Menghitungnya

Sistem Persamaan Linear Dua Variabel: Metode Gabungan Dan Metode Grafik

Originally published: September 11, 2021
Updated by Silvia Dwi