Halo Sobat Zenius, elo sudah paham belum sama nilai rata-rata? Kali ini gue mau ajak elo membahas tentang rumus rata-rata data kelompok, cara mencari dan penyelesaiannya secara lengkap.
Kita akan pakai 3 rumus yaitu dengan menggunakan titik tengah, simpangan rata-rata sementara, dan kode atau coding.
Kalau cuma baca judulnya aja sebelum loncat ke pembahasannya, keliatan kayak rumit banget ya. Sebelumnya elo masih ingat nggak apa itu data kelompok? Data kelompok adalah bentuk penyajian data yang biasanya dalam tabel dan memiliki interval tertentu.
Nah nanti kita akan belajar cara menghitung rata-rata data kelompok. Tenang aja ya Sobat Zenius, kali ini gue bakal ngejelasin rumusnya pake contoh, biar elo cepat paham. Langsung aja cekidot!

Daftar Isi
1. Rumus Titik Tengah
Contoh Soal dan Pembahasan
Tentukan nilai rata-rata dari tabel di bawah berikut ini!
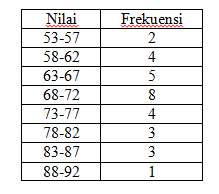
Dengan menggunakan rumus titik tengah, yang perlu dicari terlebih dahulu adalah menghitung titik tengah dari tiap kelas interval.
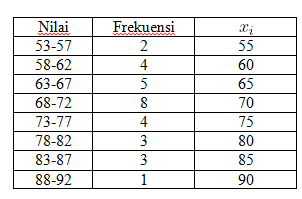
Kemudian, titik tengah tiap kelas interval dikalikan dengan frekuensinya.
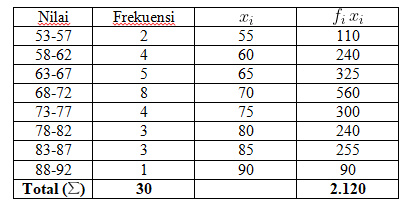
Terakhir, jumlahkan hasil tiap kelas interval dan bagi dengan total data atau frekuensi yang ada.
Jadi, nilai rata-rata dari tabel berikut menggunakan rumus nilai tengah adalah 70,67
Elo penasaran gak kalo tabel yang sama dikerjain pake rumus rata-rata data kelompok yang berbeda, apakah hasilnya bakalan sama atau beda? Cek rumus selanjutnya ya!
Biar makin paham materi ini mendingan elo langsung belajar lewat aplikasi Zenius. Elo bisa nonton banyak video pembelajaran dengan penjelasan yang mudah dimengerti. Ditambah soal latihan yang asyik banget untuk dikerjain. Buruan download aplikasi Zenius dengan klik banner di bawah ini!
2. Rumus Simpangan Rata-rata Sementara
= Simpangan ke-i (selisih antara nilai tengah dan nilai rata-rata sementara
Contoh Soal dan Pembahasan
Biar makin paham kita masih dengan tabel yang sama. Yuk coba menggunakan rumus simpangan rata-rata data kelompok. Tentukan nilai rata-rata dari tabel di bawah berikut ini!

Sebelum menghitung rata-rata data berkelompok menggunakan simpangan rata-rata, tentukan terlebih dulu rata-rata sementaranya. Sekarang, anggap nilai rata-rata sementaranya adalah 65.
Kemudian, kurangi rata-rata sementara dengan titik tengah tiap kelas interval.
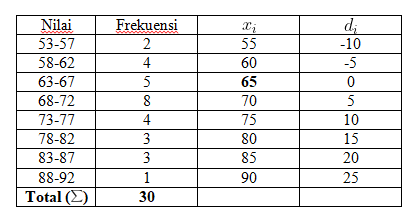
Selanjutnya, hasil pengurangan tersebut dikali dengan frekuensi tiap kelas interval.
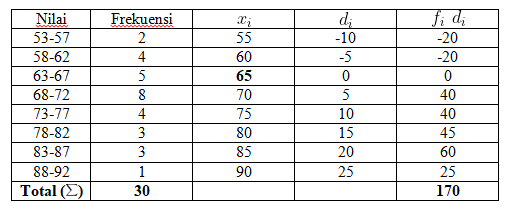
Hasil perkalian itu dibagi dengan total frekuensi semua kelas interval.
Terakhir nilai rata-rata sementara ditambah dengan hasil pembagian sebelumnya.
Dengan menggunakan simpangan rata-rata sementara nilai rata-rata tabel berikut adalah 70,67
3. Rumus Kode atau Koding
Contoh Soal dan Pembahasan
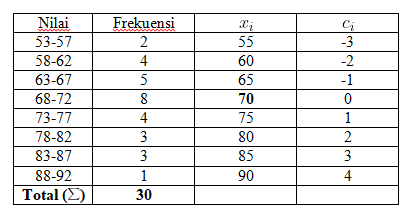
Masih dengan tabel yang sama. Tentukan nilai rata-rata dari tabel di bawah berikut ini!

Sama seperti simpangan rata-rata sementara, langkah pertama rumus coding adalah menentukan rata-rata sementara. Namun rata-rata sementara yang kita tentukan harus sama dengan nilai tengah salah satu kelas interval. Sekarang anggap nilai rata-rata sementaranya adalah 70
Pengkodean dimulai dari angka 0 untuk kelas interval yang sudah ditentukan. Kelas sebelumnya berturut-turut menjadi angka negatif. Begitu juga dengan kelas sesudahnya tapi dengan nilai positif.
Kemudian, kalikan frekuensi tiap kelas dengan kodingnya.
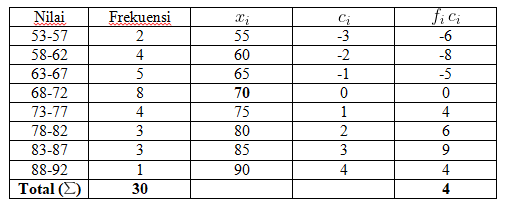
Selanjutnya, jumlah perkalian dengan koding dikali panjang interval dan bagi total frekuensi.
Terakhir, tambah rata-rata sementara ditambah hasil tersebut.
Jadi, dengan rumus koding rata-rata tabel tersebut adalah 70,67.
Wah! Ternyata pake rumus rata-rata data kelompok apapun hasilnya bakal tetep sama ya. Menurut elo di antara cara menghitung rata-rata data kelompok yang udah gue bahas, rumus apa sih yang paling mudah? Diskusi di kolom komentar ya!
Oh iya, biar belajarnya makin paham dan semangat, yuk langganan paket belajar Zenius dengan klik banner di bawah ini.
Rumus Volume Limas Segitiga dan Pembahasan Soal
Originally published: September 24, 2021
Updated by: Silvia Dwi













Pagi buk