Percaya nggak kalau 2+2 bisa jadi 10? Nah untuk kamu yang lagi belajar sistem bilangan Matematika, topik tersebut akan dikupas tuntas pada artikel ini.
Emangnya bisa ya 2 ditambah 2 hasilnya 10, bukan 4 seperti yang umum kita ketahui? Dari mana datangnya?
Nah, kalo akhir-akhir ini blog Zenius dipenuhi tulisan persiapan UN dan SBMPTN, kali ini kita santai aja dulu yuk. Gue mau mengajak lu bermain-main dengan sistem bilangan yang biasa kita pake sehari-hari. Di tulisan kali ini, gue akan memperkenalkan lu ke sistem bilangan lain, di mana 2+2 hasilnya bukan lagi 4, tapi bisa 10!
Dari balita, kita udah diajarin berhitung pake jari dari 1 sampe 10. Gedean sedikit, kita mulai mengenal bilangan 0. Sampe akhirnya kita terbiasa menggunakan sistem bilangan tersebut tanpa pernah ngeh atau bertanya-tanya kenapa harus begitu.
Tapi pernah kebayang nggak sih seandainya ada alien nih misalnya, kira-kira sistem bilangan mereka kayak apa, ya? Sama nggak dengan sistem bilangan kita? Kalau sistem bilangan kita sekarang ini kan cuma menggunakan sepuluh simbol. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, udah. Untuk bilangan setelah 9 gimana? Ya ngulang lagi aja dari 0, tapi tambahin 1 di depannya, jadinya 10. Setelah itu, lanjut lagi 10, 11, 12, 13, 14, 15, 16, 17 18, 19.
Kalau menurut ahli sejarah sih, katanya yang bikin kita punya sepuluh simbol ini karena kita punya sepuluh jari. Kalau misalkan ada alien dan jari mereka ada empat, kira-kira sistem bilangannya kayak apa yah?
Okay, lupakan aliennya. Itu cuma untuk pengantar dan sebenernya nggak ada hubungannya sama yang mau gue tulis di sini 🙂 Tapi kita bisa modifikasi sedikit pertanyaan terakhir itu:
Kalau kita cuma punya empat simbol (bukan sepuluh), kira-kira gimana sistem bilangan yang kita punya?
Sebelumnya, gue kasih tau dulu bahwa sistem bilangan yang kita punya itu namanya basis sepuluh. Basis sepuluh itu ciri-cirinya gini:
- Cuma punya sepuluh simbol
- Nggak ada satu simbol yang mewakili bilangan sepuluh
- Sepuluh itu gabungan 1 dan 0, jadi 10.
Kalau kita tulis urutan bilangannya, jadinya gini:
Sekarang, coba bayangin kalau seandainya kita cuma empat simbol. Kira-kira gimana sistem bilangan yang kita punya? Nah, sistem itu namanya basis empat. Ciri-cirinya gimana? Mirip sama basis sepuluh, tapi tinggal ganti aja kata sepuluh dengan kata empat.
- Cuma punya empat simbol
- Nggak ada satu simbol yang mewakili bilangan empat
- Empat itu gabungan 1 dan 0, jadi 10
Kebayang nggak, kira-kira konstruksi bilangannya gimana? Coba lo urutin 0, 1, 2, 3, berikutnya apa? Apa bilangan setelah 3? Karena ini adalah bilangan basis empat, jadi simbol untuk empat itu nggak ada. Untuk menunjukkan empat, kita pakai 10 (<- bacanya “satu nol” ya, bukan “sepuluh”). So, urutan bilangannya jadi gini:
[0, 1, 2, 3, 10, 11, 12, 13,…]
Setelah 13, berikutnya apa lagi?
Yup, bukan 14 yah, tapi 20. Jadi berikutnya:
[ …, 13, 20, 21, 22, 23, … ]
Terus, setelah 23? Bukan 24, tapi 30. Jadi berikutnya lagi:
[…, 23, 30, 31, 32, 33, …]
Setelah 33? Yup, berikutnya adalah 100.
[33, 100, 101, 102, 103, 110, 111, …]
Dan seterusnya…
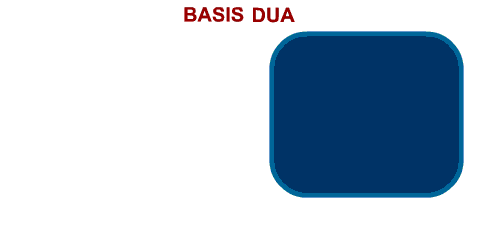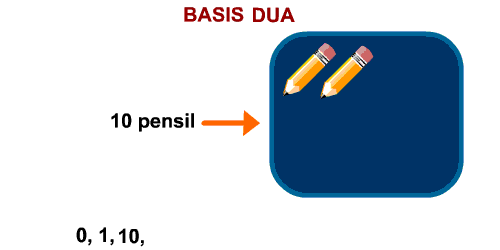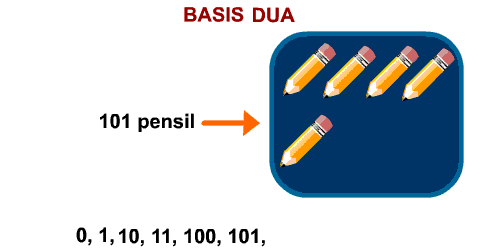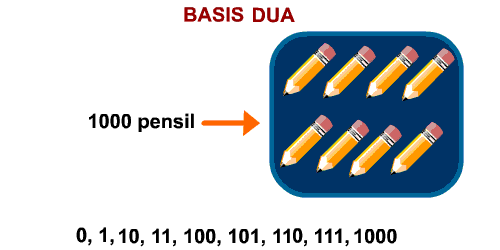
Sebagai catatan aja, 13 itu bacanya “satu tiga”, bukan “tiga belas”. Terus 20 bacanya “dua nol”, bukan “dua puluh”. 100 juga bacanya “satu nol nol”, bukan “seratus”. So… sekarang misalkan kita mau menghitung jumlah pensil pakai basis empat, berarti jadinya begini:
Lucu nggak sih? 🙂
Nah, sampe di sini, lo bisa nyambung kan dengan judul artikel ini!? Yep, 2+2 = 10 pada judul di atas ditulis menggunakan basis empat. Hehee..
Sejarah Bilangan
Sebenernya nggak semua peradaban di dunia pakai sistem basis. Salah satu peradaban yang nggak pakai sistem basis itu peradaban Romawi. Cara mereka menuliskan bilangan itu simpel banget, I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII, dan seterusnya. Cara menulis seperti ini gampang banget untuk mencacah, seperti mencacah pensil di atas. Tapi, untuk operasi yang lebih kompleks, pasti ribet banget deh. Coba aja bayangin gimana cara orang Romawi ngaliin XII dengan XVII? Yang pasti nggak pakai perkalian bersusun seperti yang kita pakai sekarang.
Salah satu teknik yang mereka pakai itu adalah tabel kayak gini:
Cara baca tabel di atas kira-kira gini: Yang warna merah itu bilangan yang dikalikan. Masing-masing elemennya dikalikan jadi yang warna hitam. Misal, X dikali X hasilnya C, X dikali V hasilnya L, dan seterusnya. Terus setelah itu digabungin semua jadi gini:
CLXXXXVVIIII
Terus gabungin V dan V jadi X.
CLXXXXXIIII
Berikutnya LXXXXX itu diubah jadi C. Sehingga jawabannya:
CCIIII
Coba cek pakai bilangan Hindu-Arab, 12 x 17 = 204. Bener kan CCIIII itu 204!
Di sini lo bisa bayangin kalau bilangan Romawi itu gampang untuk pencacahan sederhana. Tapi untuk operasi yang lebih kompleks, susahnya minta ampun. Untuk perkalian sederhana aja ribet. Makanya sistem bilangan itu kita tinggalin dan kita pakai sistem Hindu-Arab yang merupakan sistem basis sepuluh. Jauh lebih gampang untuk berbagai macam operasi.
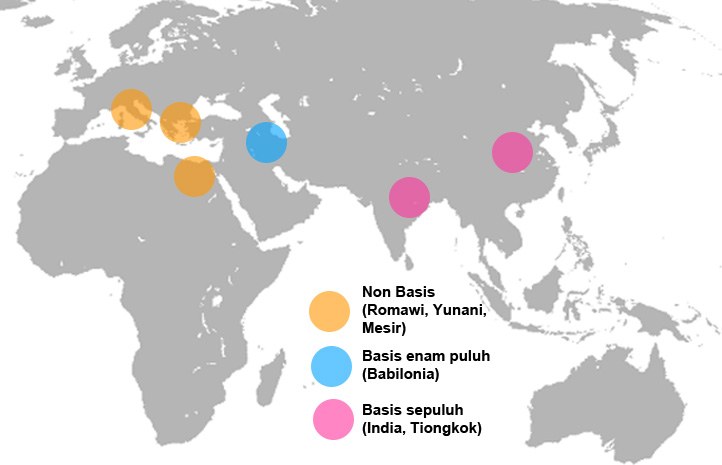
Peradaban yang sejak awal menggunakan basis sepuluh itu adalah peradaban India dan Tiongkok. Peradaban lainnya nggak pakai sistem basis, kecuali Babilonia. Gue gambarin peta masing-masing peradaban dan sistem bilangan yang mereka gunain nih:
By the way, sebagai catatan aja, peta di atas tidak menggambarkan secara akurat cakupan wilayah masing-masing peradaban yah. Selama ratusan tahun tiap peradaban tersebut eksis, cakupan wilayahnya tentunya berubah-ubah. Gue hanya melingkari pusatnya saja. Peta di atas disajikan hanya untuk mengilustrasikan pembagian wilayah penggunaan sistem bilangan.
Oiya, Pras juga pernah singgung tentang penggunaan sistem bilangan India-Arab yang menggantikan bilangan Romawi di sini.
Sistem Bilangan Babilonia
Salah satu peradaban yang menurut gue menarik itu peradaban Babilonia. Mereka pakai sistem bilangan basis enam puluh!!! Tapi bukan berarti ada enam puluh simbol. Mereka pakai basis sepuluh dulu, terus ketika sampai enam puluh, mereka ulang lagi simbolnya. Biar kebayang, coba perhatiin ini deh:
Berapa bilangan setelah 59? Gini nih:
Mirip apa coba? Yoi… mirip sistem jam, menit, dan detik yang kita pakai sekarang ini. Memang sistem pengukuran waktu jam, menit, detik yang kita pake sekarang inspirasinya dari sistem basis enampuluhnya Babilonia, udah dipakai sejak 5000 tahun yang lalu! Tapi dulu simbolnya nggak kayak sekarang. Simbol yang dulu dipakai Babilonia itu gini:
Image credit: Wikipedia
Basis Dua
Balik lagi ke basis yah. Nah, tadi kita udah coba bikin basis empat. Gimana dengan sistem bilangan basis dua? Sekarang coba lo pikirin sendiri dulu, terus coba tulis sendiri gimana mencacah pensil dengan menggunakan sistem basis dua ini. Bisa? Gue ingetin lagi prinsipnya:
- Cuma punya dua simbol
- Nggak ada satu simbol yang mewakili bilangan dua
- Dua itu gabungan 1 dan 0, jadi 10
Kebayang? Nih hasilnya:
Seru nggak sih?
Nah… basis dua itu ada nama modernnya: bit. Binary digit. Yup, sistem basis dua ini yang dipakai komputer-komputer yang ada sekarang ini. Kenapa komputer pakai basis dua? Simpel aja, karena komputer cuma bisa tau dua kondisi, yaitu 1 dan 0. Di listriknya, bisa jadi 1 itu adalah kondisi ketika tegangan positif, 0 itu untuk tegangan negatif, gitu. Bisa juga 1 itu kondisi ada arus dan 0 itu kondisi nggak ada arus. Kalau di harddisk, biasanya 1 dan 0 itu simbol untuk arah kutub magnetnya, karena data kita disimpan di harddisk dalam bentuk magnet ini, kutub utara atau selatan.
Nah, sekarang coba kita perhatiin ini deh:
0 basis dua = 0 basis sepuluh
10 basis dua = 2 basis sepuluh
100 basis dua = 4 basis sepuluh
1000 basis dua = 8 basis sepuluh
10000 basis dua = 16 basis sepuluh
100000 basis dua = 32 basis sepuluh
1000000 basis dua = 64 basis sepuluh
10000000 basis dua = 128 basis sepuluh
100000000 basis dua = 256 basis sepuluh
1000000000 basis dua = 512 basis sepuluh
10000000000 basis dua = 1024 basis sepuluh
Itu adalah kelipatan 2 semua. Makanya kalau kita beli harddisk, RAM, atau perangkat komputer lainnya, biasanya bilangannya itu adalah bilangan kelipatan dua seperti di atas.
Kalo lo tertarik masuk jurusan Ilmu Komputer/Teknik Informatika, lo bakal pelajari bilangan basis dua (binary) ini nanti di semester awal perkuliahan lho.
Satuan, Puluhan, Ratusan, ….. pada Berbagai Sistem Bilangan
Pada bilangan basis sepuluh, kita mengenal satuan, puluhan, ratusan, dan seterusnya. Misalnya kita punya 367, itu artinya adalah: [latexpage]
$$367 = 300 + 60 + 7$$
$$= 3 \times 100 + 6 \times 10 + 7$$
Nah, pada basis lain seperti basis dua atau basis empat, konsepnya juga sama aja. 10010 pada basis dua misalnya, bisa ditulis begini:
$10010_{(2)} = 10000_{(2)} + 10_{(2)}$ (basis dua)
Jadi ketika kita mau konversi bilangan itu ke basis sepuluh, kita tinggal bikin begini:
$$10010_{(2)} = 10000_{(2)} + 10_{(2)} = 16 + 2 = 18$$
(tanda kurung $(2)$ itu menunjukkan kalau dia sistem basis dua, kalau nggak ada tanda kurungnya berarti basis sepuluh)
Untuk basis empat, misalnya bilangan 321, gimana konversinya?
$321_{(4)} = 300_{(4)} + 20_{(4)} + 1_{(4)}$ ($\leftarrow$ basis empat)
$= 3 \times 100_{(4)} + 2 \times 10_{(4)} + 1_{(4)}$
$= 3 \times 16 + 2 \times 4 + 1$ ($\leftarrow$ basis sepuluh)
$$= 48 + 8 + 1$$
$$= 57$$
By the way, trik penting dari konversi di atas adalah lo mengganti $100_{(4)}$ jadi 16 dan $10_{(4)}$ jadi 4. Karena 100 di basis empat itu adalah 16 di basis sepuluh, dan 10 di basis empat itu adalah 4 di basis sepuluh.
****
Okay deh. Sekarang, kalau lo mau iseng-iseng ngetes seberapa jauh pengertian lo terhadap bilangan basis ini, coba konversi bilangan basis di bawah ini jadi bilangan basis sepuluh. Tulis di comment yah jawabannya.
231 basis empat = … basis sepuluh
1010110 basis dua = … basis sepuluh
3210023 basis empat = … basis sepuluh
102930 basis duabelas = … basis sepuluh
Terus sekarang coba dibalik (yang ini lebih susah karena belum gue kasih tau triknya, tapi ya boleh dicoba lah):
89 basis sepuluh = … basis empat = … basis dua = … basis duabelas
190 basis sepuluh = … basis empat = … basis dua = … basis duabelas
823 basis sepuluh = … basis empat = … basis dua = … basis duabelas
Selamat mencoba 🙂
==========CATATAN EDITOR===========
Kalo ada di antara lo yang mau menjawab tantangan Wisnu, silakan tinggalin jawaban kamu di bawah ya. Kalo kamu mau nanya-nanya lebih lanjut sama Wisnu tentang basis bilangan, langsung aja tinggalin komentar di bawah artikel ini ya.











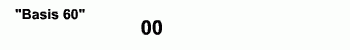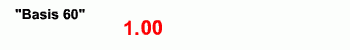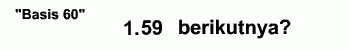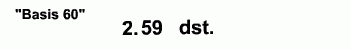

Bingung Bang Wisnu hehe 😉
Hehe… yah coba baca sekali kali kalau gitu biar nggak bingung. Bagian yang paling bikin bingung yang mana?
Gie kerjain yang bawah ya bang,
89(10) = 1121 (4) = 1011001(2) = 75(12)
190(10)= 2332(4) = 10111110(2) = 13 10 (12)
823(10)= 30313(4) = 10110110111(2) = 587(12)
*maaf kalo salah hitung mata gue udh sayup-___-
Caranya gampang kalo buat basis sepuluh mau dikonversikan ke basis lain tinggal bagi aja sama basis yang dituju. Bagi sama bilangan terdekat nah kan ada sisanya tuh, urut deh sisanya dari bawah dan itulah hasinya.
Ex: 22(10) = …. (2)
22/2 = 11 sisa 0
11/2 = 5 sisa 1
5/2 = 2 sisa 1
2/2 = 1 sisa 0
1/2 = 0 sisa 1
Hasilnya 22 basis sepuluh(10) adalah 10110 basis dua (2)
ohh gitu caranya cptnya.. gue malah di urut -_-
Ngurutin bilangan itu emang cara awal untuk ngerti maksud bilangan basis. Kalau ini adalah pertama kalinya lo kenal konsep basis tapi udah bisa ngurutin dengan bener, menurut gue sih udah lumayan banget yah. Hehehe…
Nice. Caranya bener. Hasilnya juga bener semua kecuali yang 823. Basis duanya harusnya 11 0011 0111. Paling nggak teliti aja sih.
Terus untuk basis 12, biasanya setelah 9 itu kita bisa pakai A dan B. Jadi A itu untuk sepuluh dan B itu untuk sebelas. Jadi kalau simbolnya begitu, untuk yang 190, basis duabelasnya jadi 13A. Tapi dengan lo nulis 13 10 malah kelihatan sih kalau lo ngerti konsepnya. Cool.
Bukannya A itu untuk satu nol dan B itu untuk satu satu ya? bukan sepuluh dan sebelas.. xixixixixxii
Bukan, men. Yang bener sepuluh dan sebelas untuk A dan B. Kalau “satu nol” dan “satu satu” basis dua belas itu kan 12 dan 13 basis sepuluh. Urutannya begini:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, 10, 11, 12, ….
hahahah… *kibar bendera putih* thanks ilmunya.. gue udah masuk semester 4 di teknik dan baru tau yang kaya gini… wakakakakakak payah gue…
Tuh bener ada salah hitung lg mau tidur eh baca blog ini soalnya haha
Nah itu gue galau yg basis 12 takutnya beda sm basis 16, jadi gue nulisnya pisah deh yg 13 10.
Oh jadi hampir sm kaya basis 16 buat A,B setelah 9. Oke deh ilmu baru, thanks kak wisnu(y)
Yo. Sama-sama.
Terus klo basis 16 urutannya gimana gan?
Apa 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,10,11,12….dst?
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, … dst
(Lo cuma kurang F aja. F itu kan 15 basis sepuluh).
abis bolak-balik itungannya gw dapat jawaban yg
beda
89 basis 10 = 705 basis 12
190 basis 10 = 10310 basis 12
823 basis 10 = 50807 basis 12
jawaban lain sama, hehe #toss
karena 12 basis 10 itu udah 100 basis 12, bukan 10 lg. trus 12^2 jadinya 10.000, bukan 100.
CMIIWW
tapi alasannya kenapa ya? mungkin bang Wisnu bisa jawab 🙂
Okeh toss dulu #toss
By the way 12 basis 10 itu 10 basis 12 mas.. 12(10) = 10(12)
Kalo gue ngerjain urutan lebih suka simple kaya gini (gue coba balikin ya)
10(12) = …. (10)
= 1.(12)^1 + 0. (12)^0
= 12 + 0
= 12 (10)
Logikanya jg udah keliatan kok basis 10 sm basis 12 kan banyakan(lebih gede gitulah) basis 12
jadi hasilnya jg pasti lebih banyak yang basis 10 dibanding basis 12.
Nah coba kalo jawabannya gue balik sebagai pembuktian ya
705(12)= …. (10)
= 7.(12)^2 + 0.(12)^1 + 5(12)^0
= 1008 + 0 + 5
= 1013(10) *nah hasilnya malah segitu bukan 89, coba yg lainnya dicobain
tuhkan bener, ada. Di zenius tuh belajar kayak ga ada yang mustahil. Semua ada, asal ada hipotesis dan evidence = Teori
Keren 🙂
di smk teknik elektronika di sekolah gue jg diajarin, yg basis 2(biner), basis 8(oktal), sama basis 16(hexa), termasuk operasinya. . . :3
Nah, mantab itu. Btw, hati-hati salah kaprah, hexa itu artinya 6. Kalau 16 itu hexadesimal.
Haha keren bang!
Thanks yah
sistem bilangan yang dibuat zaman Mesir, yang ditulis di tablet Naqada, lebih ribet dari ini. Eh, kalo ngga salah dulu zamannya Phytagoras angka nol belum ketemu kan? Gila aja itu ngitungnya kayak gimana..
Nah, ini nih yang seru juga. Mesir itu sistem bilangannya nggak pakai basis, sama kayak Romawi dan Yunani. Angka nol nggak ada. Yang lebih gokil lagi, pecahan model A/B seperti yang kita punya sekarang juga belum ada. Tapi mereka punya bentuk 1/N, jadi kayak pecahan sekarang, cuma pembilangnya selalu 1.
Dengan sistem yang begini aja udah bisa bikin macem-macem. Phytagoras gitu-gitu menghitung dengan sistem bilangan model begini. Rada seru juga untuk diangkat jadi satu artikel sendiri sih sebenernya.
nih bang, yg atas ampe no 3 aje ye, males haha
1) 200+ 30+ 1=
32+12+1= 45
2) 1000000+ 10000+ 100+ 10=
64+ 16+ 4+ 2= 86
3) 3000000+ 200000+ 10000+ 20+ 3=
3*4096+ 2*1024+ 1*256+ 2*4+ 3
12288+ 2048+ 256+ 8+ 3 =14603
Sip. Bener semua 🙂
Ini bang, koreksi yak.
Untuk yang tantangan 3 soal selanjutnya agak rempong juga sih gw. Tapi gw nyarinya dengan cara basis berapa yang dicari, maka dicari operasi hitungnya, kayak di gambar. Misal dari basis 10 dicari basis 12, maka gimana caranya biar itu bilangan ada bilangan 12 dan kelipatannya, kayak 12, 144, 1728 dimana masing2 bilangan basis 10 nya adalah 10, 100, 1000, dll. Capek sih jadi ga kerjain semuanya, tapi pemahaman gw bener gak bang?
Sekalian nambahin deh untuk angka 190 deh ke basis 12 :
190 = 144 + 46
= 144 + 3.12 + 10.1
= 100 + 30 + 10 = 140
Mantabs nih. Untuk yang 4 soal pertama (konversi basis n ke basis sepuluh) caranya bener semua. Cuma soal nomor satu kurang teliti aja. 32 + 12 + 1 itu harusnya 45, bukan 63.
Untuk soal berikutnya (konversi sebaliknya, basis sepuluh ke basis n), lo harus pakai teknik yang berbeda. Kalau pakai teknik yang sama, hasilnya jadi salah. Contoh, yang 89, dikonversi ke basis empat jadinya 521 itu pasti salah, karena pada basis empat nggak ada angka 5. Iya nggak? 🙂
Btw, kalau lo mau coba nemuin tekniknya, coba mulai dari yang sederhana deh. Misalkan lo mau konversi 5 basis sepuluh ke basis empat. Lo udah tau jawabannya 11(4) dari ngurutin. Sekarang kira2 gmn tekniknya kalau tanpa ngurutin? Misal, lo coba2 bagi 5 dengan 4, lihat hasil bagi dan sisanya.
Terus coba lagi bilangan yang lebih gede lagi. 9 basis sepuluh misalnya. Bisa nggak pakai metode pembagian tadi untuk dapetin hasilnya? (lo bisa tau hasilnya harusnya berapa dari ngurutin)
Bang glen, Sbmptn kan tinggal 2,5 bulan lg. Nah, gw belajar baru 3
minggu yg lalu. gw ikutin tuh sarannya bang sabda di xpedia guide/zlg
“sebelum lo denger pembahasan, lo mesti ngerjain contoh soalnya dulu”.
Pas gw review materi terus mau ngerjain contoh soalnya gw selalu gak bisa.. terus gw denger sampe habis penjelasannya. nah, setelah habis penjelasan contoh soal, gw coba ngerjain dibuku soal yg lain kok gw tetep jg gak bisa bang ? Please tolongin guaa…
ga ngerti bang -____-
Ceritain dong bagian nggak ngertinya di mana. Bisa gue perbaiki tulisannya kalau masih ada yang bikin bingung.
niat banget nulisnya
emang zenius deh km
Niat dong. Nulisnya pakai hati soalnya.
Kayak pemograman basis data 🙂
Hmm.. kayak biner kali maksudnya. Kalau “basis data” itu beda lagi soalnya. Tapi ya, basis ini, terutama basis 2 (biner), memang dipakai banget di pemrograman, di artikel di atas juga dijelasin kenapa.
bang mohon dikoreksi ,(pake kalkulator hehe :’| )
Sip. Udah bener semua kok. Teknik dan jawabannya bener.
akhirnya gua ngerti maksud dari bilangan basis, pernah belajar bil basis 10(2) tapi gatau konsep nya gimana thanks bang Wisnu !! 🙂
Yo. Sama-sama yah.
Keren artikelnya bang! udah gw jawab tuh semua soalnya..
btw mau tanya bang Wis, kalo kasusnya lain, misalnya bilangan desimal koma basis sepuluh di konversi ke biner, caranya sama gak bang atau beda?
thanks!
Pertanyaannya bagus banget nih. Kalau sebaliknya, biner ke basis sepuluh, masih gampang.
Misal kita punya 10,11, langsung aja kita ubah jadi gini:
10,11(2) = 10(2) + 0,1(2) + 0,01(2)
=4 + 1/2 + 1/4
=4,75
Kebayang? Jadi 0,1 basis dua itu 2 pangkat -1 sementara 0,01 basis dua itu 2 pangkat -2, dan seterusnya. Masih belum teralalu susah sih.
Nah, sekarang kalau sebaliknya gimana? Itu yang rada repot.
4,75 basis sepuluh kalau diubah jadi basis dua gimana caranya? Enaknya pisahin dulu sih 4 sama 0,75nya. Untuk 4 bisa dicari pakai cara di atas (di comment2 dibahas konversi basis sepuluh ke basis lain). Untuk 0,75nya gimana? Itu rada panjang jelasinnya, tapi kalau mau tau, coba baca artikelnya di sini deh.
btw..bilangan basis2 gini dipelajarin dimana? terus kegunaanya selain utk komputer ada lagi gk bang?
Sekarang di kurikulum sih nggak ada. Tapi jaman gue dulu, guru SD gue pernah ngasih ini sebagai pengayaan. Gue inget gara-gara belajar beginian, gue melihat gigi sepeda gue bagaikan bilangan basis seandainya penomorannya dari nol, tepatnya basis enam karena gigi roda belakangnya ada enam.
Kalau ditanya gunanya secara langsung sih kayaknya nggak ada yah. Tapi belajar basis ini bisa membangun abstraksi yang bagus tentang konsep bilangan. Jadi semacam ngebuka pandangan kita terhadap konsep bilangan, dan bisa ngebedain antara angka dengan bilangan yang direpresentasikan oleh angka tersebut. (Btw, kebayang nggak sekarang bedanya antara angka dan bilangan?) Nah, ngebangun abstraksi-abstraksi baru kayak gitu adalah salah satu hal yang bisa meningkatkan kecerdasan juga. Kalau penasaran apa hubungannya, bisa juga baca artikel zenius yang satu ini.
mantep bang !!!, sering-sering share yang seru kaya gini yaaa
Sip. Diusahain yah. Hehe…
nice bang 🙂
Thanks yah
stress sendiri gua liatnya, gimana mau ikutan ngitung. otaknya udah cape buat ngitung fisika HAAHAHA. Besok TO nich -_- *Curhat
Thanks artikelnya kak, kapan2 ane balik lagi buat liat lebih serius 😀
Hehe… yah, nanti kalau udah lebih santai bisa balik ke sini lagi untuk baca lebih serius 🙂
bang aku bingung deh habis 33 kok bisa 100 tu caranya gimana ya ?
Kan itu basis empat, jadi nggak ada angka 4. Setelah 3, angkanya jadi 10 (satu nol). Terus setelah 33, kita pakai 100.
Sama aja sih dengan basis sepuluh. Karena nggak ada angka sepuluh, jadi setelah 9, kita pakai 10. Terus setelah 99, jadinya 100. Kebayang?
Yg basis 60 gw koq cuma liat 59 bilangan yah?
Yup. Soalnya dulu belum dikenal angka nol. Kalau ada angka nol di awal, jadinya ada 60.
Karena mereka nggak punya angka nol, kalau muncul angka nol di tengah (misal 502), paling mereka pakai spasi kosong aja di tengah-tengahnya.
Bang wisnu, Sbmptn kan tinggal 2,5 bulan lg. Nah, gw belajar baru 3
minggu yg lalu. gw ikutin tuh sarannya bang sabda di xpedia guide/zlg
“sebelum lo denger pembahasan, lo mesti ngerjain contoh soalnya dulu”.
Pas gw review materi terus mau ngerjain contoh soalnya gw selalu gak bisa.. terus gw denger sampe habis penjelasannya. nah, setelah habis penjelasan contoh soal, gw coba ngerjain dibuku soal yg lain kok gw tetep jg gak bisa bang ? Please tolongin guaa…
Keren bang. Bisa buat tebak tebakan sama temen hehe シ
men, masih bingung itu yg basis 10 dikonversi ke basis 4, 2, atau 12 gmna carany?
ga ngerti”.
begindang bukan ka wisnu?
Mas Wisnu, sekarang di K13 ternyata ada materi Transmisi dan Penyimpanan Data lho.. Wah, bisa dijadikan referensi ini.. Makasih Mas! 😀
Kak,, aku kan masih SMA kls1 nigh
Aku coba kerjain soal yang atas dulu yahh
231(4)=45(10)
1010110(2)=86(10)
3210023(4)=14603(10)
102930(12)=253620(10)
Itu jawabanku, banget ga kak?
Oh ya,, aku belum ngerti cara ngerjain soal yang bawah, tapi aku lagi berusaha ngerjain dengan cara yang dikasih kakak2 di komen^^
Ohhhh,, sekarang aku juga udah ngerti gimana cara ngerjain soal yang bawah^^
Makasih kakak2 semuaaa^^
gua di smk diajarin cara ngitung beginian tapi baru tau “PAHAM” apa itu basis sekarang stelah baca artikel ini…thankyou zenius
aku baru belajar kaya gini karna dapat elins di sem3. kayaknya kalo bahas gerbang logika atau aljar boolean seru juga tuh bang, ada tabel truth, ada rangkaian seri paralel juga kan, apalagi sama timing diagram
Bang, lain kali tulis sumbernya dari buku atau jurnal apa biar saya juga langsung baca di sumbernya
mantap Bang 😀 https://uploads.disquscdn.com/images/597a40cf5d3135a37224c3291200bf819fa5222d0860e92c9734c9328cf5083a.gif
Anjay , sistem bilangan .
Aku tau nih, di pelajaran sekolah kan ada ?
Btw ,aku anak smk , SMK Bisa !! Yess . Haha
231 basis empat = 45 basis sepuluh
1010110 basis dua = 86 basis sepuluh
3210023 basis empat = 14603 basis sepuluh
102930 basis duabelas = 253620 basis sepuluh
Bener ga bang? Bantuan kalkulator sih, angkanya gede xD
Kalo yang bawah itu tinggal bagi, terus sisa-sisanya jadi hasil ya, kebetulan dulu waktu masih smk ada pelajaran konversi bilangan kayak gini