Apakah Superman bisa mengunakan sedotan untuk menghisap air dengan kedalaman 11 meter? Pertanyaan ini dijawab dengan pendekatan Fisika, khususnya konsep Fluida Statis!
Pusing banget deh makin banyak belajar, makin banyak juga rumus yang harus dihapalin! Hayoo… elo mikir gini juga nggak? Kalau elo cuma ngapalin rumus, ngapalin huruf-hurufnya aja tanpa tahu dari mana rumus itu berasal, ya pasti elo bingung.
Elo harus tahu dulu nih, apa sih yang membuat rumus itu ada. Yuk kita pelajari pelan-pelan.
Pengertian
Pertama-tama coba kita pahami materi ini dari kata per kata. Ada kata tekanan dan kata fluida. Kita bahas fluida dulu ya.
Fluida
Fluida adalah zat yang bisa berubah bentuk secara terus menerus. Fluida bisa berbentuk zat cair atau zat gas. Jadi, bisa diartikan bahwa kali ini kita akan belajar tentang hukum fisika yang berlaku pada zat cair atau zat gas. Fluida dibagi menjadi dua, yaitu fluida statis dan fluida dinamis.
Fluida statis adalah zat gas atau zat cair yang diam. Contohnya adalah zat cair di dalam gelas atau bisa juga air di dalam ember.
Fluida dinamis adalah zat gas atau zat cair yang bergerak dan memiliki kecepatan tertentu. Nah lho, gimana tuh maksudnya? Contoh fluida dinamis adalah air yang keluar dari ember yang bocor.
Ngomong-ngomong fluida statis, beberapa waktu yang lalu ada murid yang ngasih pertanyaan menarik. Pertanyaannya gini:
Bisa nggak Superman menggunakan sedotan untuk menghisap air yang kedalamannya 11 meter?
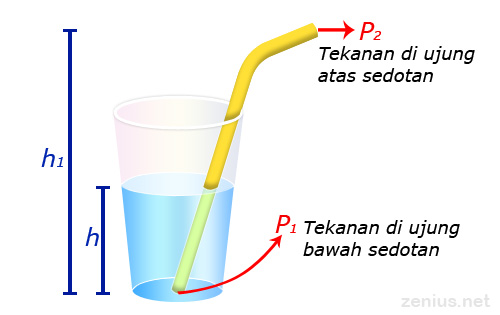
Sebelum kita jawab pertanyaan itu, kita harus tau dulu nih, apa sih yang bikin kita bisa menyedot air minum pakai sedotan. Jadi konsepnya gini. Kalau sedotannya cuma kita masukkan ke dalam gelas, maka nggak ada air yang keluar kan? Kenapa bisa begitu? Karena perbedaan tekanan antara dasar sedotan dengan ujung atas sedotan nggak cukup besar untuk mengangkat air ke atas. Biar kebayang maksudnya gimana, coba lihat gambar di bawah.
Di gambar, gue kasih label P₁ dan P₂ berturut-turut untuk tekanan di dasar sedotan dan tekanan di ujung atas sedotan. Nah, besar P₁ bisa dicari dengan persamaan ini:
Di mana P₀ itu tekanan udara di atmosfer, 𝜌 massa jenis air, dan h₁ kedalaman air. Bagian 𝜌.g.h₁-nya itu adalah tekanan hidrostatis. Apa lagi nih tekanan hidrostatis? Yuk, kita cari tahu dulu pembahasan tentang tekanan.
Tekanan
Nah, kalau ngomongin ilmu fisika, yang dimaksud dengan tekanan adalah gaya yang diberikan pada permukaan tertentu. Tekanan bergantung pada besarnya daya. Semakin besar daya-nya, semakin besar juga tekanannya. Jadi, dari kalimat ini bisa diambil rumusan seperti berikut:
Rumus Tekanan Secara Umum
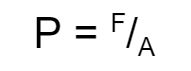
P = tekanan
F = gaya, dengan satuan newton (N)
A = luas permukaan atau luas penampang, dengan satuan meter persegi (m2)
Nah, karena rumus tekanan adalah gaya per luas permukaan, maka satuannya adalah N/m2 atau bisa juga disebut sebagai pascal yang disingkat menjadi (Pa). Rumus di atas ini adalah rumus tekanan secara umum. Nanti, akan ada rumus-rumus turunannya lagi guys. Jangan pusing dulu ya. Pokoknya elo pahami rumus dasar ini dulu.
Nah, tekanan dibagi lagi menjadi beberapa jenis. Rumusnya pun beda-beda.
1. Tekanan Hidrostatis
Tekanan hidrostatis adalah tekanan yang disebabkan oleh zat cair.
Coba lihat gambar di bawah ini. Ada benda A dan benda B.
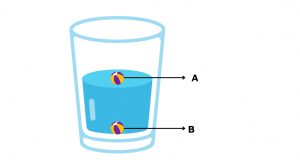
Benda A mengapung di atas air sedangkan benda B berada di dasar air. Dari sini, elo tahu nggak, yang mana benda yang memiliki tekanan paling besar? Nah, pinter. Jawabannya adalah benda B.
Benda A memberikan tekanan dari luar, yaitu tekanan atmosfer. Nah, pada benda B ada tekanan atmosfer dan juga tekanan hidrostatis. Kalau mau dirumuskan, berarti kayak gini nih rumusnya.
Tekanan Benda A = Tekanan Atmosfer (Pa = Po)
Tekanan Benda B = Tekanan Atmosfer + Tekanan Hidrostatis (Pa = Po + Ph)
Sampai sini paham? Oke lanjut. Tekanan hidrostatis itu tergantung pada kedalaman air. Semakin dalam airnya, semakin kuat juga tekanannya. gitu, gimana kalau mau menghitung tekanan hidrostatis di kedalaman tertentu? Ini dia rumus tekanan hidrostatis.
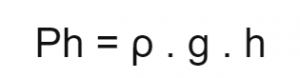
Ph = tekanan hidrostatis (N/m2 atau Pa)
Ρ = masa jenis zat cair (kg/m3)
g = percepatan gravitasi (m/s2)
h = kedalaman zat cair (m)
2. Tekanan Gauge
Tekanan Gauge adalah tekanan yang tidak dipengaruhi oleh tekanan atmosfer. Contohnya adalah tekanan gas pada ban. Untuk mengetahui tekanan gauge, elo bisa menggunakan rumus tekanan gauge di bawah ini:
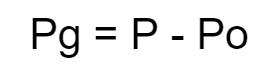
Pg = tekanan gauge
P = tekanan mutlak
Po = tekanan atmosfer
-
Tekanan Mutlak pada Zat Cair
Nah, setelah mempelajari tekanan hidrostatis dan tekanan gauge, pasti bakal ada pertanyaan gimana cara mencari tekanan mutlak pada zat cair? Ini dia rumus tekanan mutlak
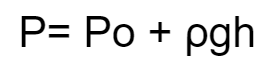
P = tekanan Mutlak (N/m2 atau Pa)
po = tekanan udara luar (N/m2 atau Pa)
ρ = massa jenis zat cair (kg/m3)
h = kedalaman zat cair (m)
g = percepatan gravitasi (m/s2)
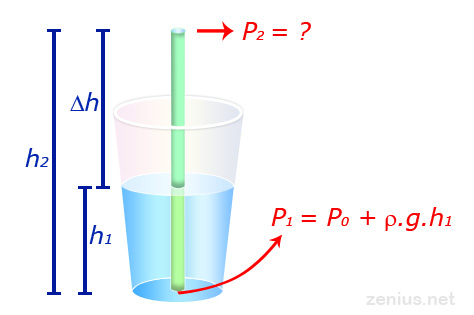
Kalau sedotannya didiemin aja, maka tekanan pada P₂ akan sama dengan tekanan atmosfer, yaitu P₀. Dan ini nggak akan cukup untuk mengangkat air ke atas. Sekarang, supaya air bisa tersedot ke atas, berapa besar tekanan di P₂? Kita lihat lagi gambarnya di bawah :
Gambar tersebut adalah kondisi di mana air bisa terangkat ke atas. Dari gambar, kita bisa lihat kalau P₂ bisa dihitung:
ΔP = P₁ – P₂ = 𝜌.g.h₂
Di mana h₂ itu adalah tinggi sedotan (jarak dari dasar sedotan ke bagian atas sedotan). Kalau gitu kita substitusi persamaan (1) ke P₁, sehingga:
$ \begin{align} P_0 + \rho.g.h_1-P_2 &= \rho.g.h_2 \nonumber \\ P_2 &= P_0 – \rho.g.(h_2-h_1) \nonumber \\ P_2 &= P_0 – \rho.g.\Delta h \end{align} $
Jadi nilai P₂ sebenernya cuma bergantung sama Δh aja, yaitu jarak antara permukaan air ke ujung atas sedotan. Variabel lainnya biasanya udah fixed. Misalnya kita mau menyedot air di gelas dengan jarak Δh = 10 cm (atau 0,1m), berarti dari persamaan (2) kita bisa langsung hitung nilai P₂ gini:
$ \begin{align*} P_2 &= P_0 – \rho.g. \Delta h \\ &= 10^5-(1000)(10)(0,1) \\ &= 10 \times 10^4 – 0,1 \times 10^4 \\ &= 9,9 \times 10^4 Pa \end{align*} $
Nah, jadi kita cuma butuh membuat tekanan di mulut menjadi 9,9 x 10⁴ Pa untuk bisa menyedot air tersebut. Btw, ini sebenernya perhitungan kasar aja yah. Angka-angka yang dimasukin juga pakai pembulatan (seperti angka gravitasi dan tekanan udara*). Tapi, yang penting lo dapet konsepnya lah.
[expand title=”sedikit catatan tentang pembulatan gravitasi dan tekanan udara (klik aja)”]
*) Di perhitungan ini, gue pake nilai tekanan udara P₀ = 10⁵ Pa dan gravitasi g = 10 m/s². Tapi sebenernya tekanan udara dan gravitasi ini beda-beda di setiap tempat, dan angka yang lebih akurat adalah P₀ = 1,01 x 10⁵ Pa dan g = 9,8 m/s². Dan untuk simplifikasi, perhitungan ini juga mengabaikan aturan angka penting.
[/expand]
Ketika kita menggunakan sedotan, diafragma di bawah paru-paru kita turun, sehingga paru-paru mengembang dan membuat tekanan udara di paru-paru turun. Ini juga membuat tekanan udara di mulut turun.
Sekarang kita bisa balik lagi ke pertanyaan awal. Superman bisa nggak ya menyedot air kalau kedalamannya 11 meter?
Superman kan hebat banget. Anggap aja dia bisa bikin tekanan udara di mulutnya keciiil banget, sampai nol. Hal ini bisa terjadi kalau Superman bisa bikin mulutnya menjadi hampa udara (vacuum). Kalau gitu, kita masukin aja nilai P₂ = 0 ke persamaan (2) untuk mencari nilai Δh yang mungkin. Coba yah.
$ \begin{align*} P_2 &= P_0 – \rho.g. \Delta h \\ 0 &= 10^5-(1000)(10)(\Delta h) \\ \Delta h &= \frac{10^5}{1000.10} \\ &= 10m \end{align*} $
Jadi kelihatan kan kalau kedalaman maksimum untuk menyedot air itu adalah 10 meter. Artinya, kalau dia mau menyedot air yang kedalamannya 11 meter, dia harus membuat tekanan di mulutnya menjadi kurang dari nol, which is impossible.
Tapi ya… namanya juga Superman. Dia udah berkali-kali melanggar hukum Fisika di komiknya. Jadi, kalau si pengarang komik ini bikin cerita tentang Superman yang bisa menyedot air di kedalaman 11 meter, sah-sah aja. Dan tergantung fantasi lo juga Superman ini bisa atau nggak 🙂
Contoh Soal
Tadi elo udah belajar teori. Rumus juga udah dikasih semua. Nah, biar elo makin paham, yuk kita kerjain contoh soal tekanan fluida di bawah ini!
1. Sebuah kolam renang memiliki kedalaman 5 meter. Berapa tekanan hidrostatis pada dasar kolam jika ρ air = 1000 kg/m3 dan g= 10m/s2?
Jawabannya adalah
Ph = ρ . g . h
Ph = 1000.10.5
Ph = 50000 N/m2
2. Terdapat sebuah batu dalam zat cair dengan massa jenis 300 kg/m3 dan tekanan hidrostatis 300 N/m2. Diketahui percepatan gravitasi bumi adalah 30m /s2. Di kedalaman berapa batu tersebut jatuh?
Jawabannya adalah
Ph = ρ . g . h
300 = 300.30.h
h = 300/300 . 30
h = 0.3 meter atau 30 cm.
Gimana sob? Jawaban elo bener semua atau salah semua nih? Mungkin artikel ini memang membahas di permukaan doang, tapi jangan sedih, elo bisa nonton penjelasan tutor sejelas-jelasnya lewat video pembelajaran. Yuk klik banner di bawah ini. Lengkap dengan soal juga lho!
Nggak usah pusing kalau masih banyak materi yang belum elo pahami di sekolah. Elo bisa berlangganan Zenius. Klik banner di bawah ini untuk tahu paket belajarnya!












bang, gimana yah ngatasin masalah pemodelan2 rumus gitu?
entah kenapa suka pedih mata gue pas liat rumusnya sama suka kusut juga..
yang gue khawatirkan nanti di perkuliahan yg gue rasa perumusan2 kayak gitu lebih advance bahaya deh kalau gak ngerti apalagi banyak di buku2 main hajar rumus aja.. jadi gimana yah ngatasin masalah itu? 🙂
Jawaban simplenya sih… practice. Hehehe…
Mulai dari coba-coba nurunin sendiri setiap kali ada persamaan. Ini udah lo lakuin kan? Terus nanti kelihatan konsep ini nyambungnya ke mana, bisa diutak-atik gimana persamaannya, dst. Semakin sering latihan, semakin jago sih.
ini dia serunya! 🙂
Btw, gue tambahin dikit. Pompa air listrik yang biasa di rumah-rumah juga sebenernya pakai konsep ini. Kalau pompanya hampa udara, maka dia bisa ngangkat air yang kedalamannya 10m. Tapi nggak akan bisa lebih dari itu. Real-nya sih, pompa air lisrik setau gue paling cuma bisa dipakai untuk kedalaman 6-7m. Mungkin karena nggak bener-bener hampa udara kali.
oh jadi asalnya rumus pers bernoulli dr situ ya…
sama guru cuman dikasih rumus jadinya doang -_-
kalo menurut logika saya sih bisa aja asalkan sedotannya pendek terus ujungnya cuma sampe dipermukaan yang pentingkan airnya kedalamannya 11 meter bukan sedotan yang panjangnya 11 meter wkwk
Hehe. Nice counter.