Hi Sobat Zenius, masih ingat enggak nih rumus keliling dan luas segitiga? Semasa Sekolah Dasar, kita sudah pernah belajar cara menghitung keliling dan luas segitiga. Di SMP elo bakal belajar tentang segitiga lebih dalam lagi.
Enggak usah pakai lama, yuk bareng gue belajar jenis segitiga, rumus luas segitiga, rumus keliling segitiga beserta contoh soal segitiga.
Apa sih segitiga itu? Segitiga adalah bangun datar yang dibuat dari tiga sisi yang berupa garis lurus yang saling saling berpotongan dan tiga sudut yang tidak segaris. Elo perlu inget nih, jumlah ketiga sudut suatu segitiga ialah 180°.
Daftar Isi
Jenis-Jenis Segitiga Berdasarkan Panjang Sisi
Segitiga banyak jenisnya, lho. Perbedaan jenis segitiga yang satu ini berdasarkan panjang di setiap sisinya.
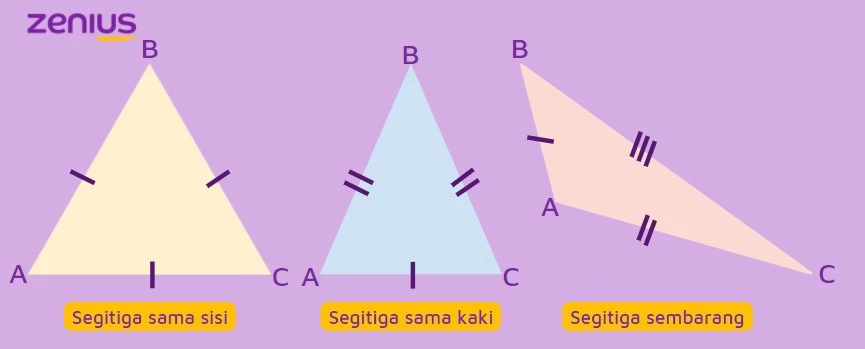
Segitiga Sama Sisi
Segitiga sama sisi adalah segitiga yang ketiga sisinya sama panjang. Karena sisinya sama panjang, 3 buah sudutnya juga sama besar.
Perhatikan gambar segitiga ABC yang merupakan contoh segitiga sama sisi.
AB = BC = AC
Sudut A = sudut B = sudut C
Diingat ya rumus keliling segitiga sama sisi di atas.
Untuk mempelajari segitiga sama sisi beserta rumus lengkapnya, klik link berikut: Rumus Segitiga Sama Sisi – Luas dan Keliling.
Segitiga Sama Kaki
Segitiga sama kaki adalah segitiga yang dua di antara sisi segitiganya sama panjang. Enggak cuma itu, segitiga sama kaki juga memiliki sepasang sudut yang sama besar.
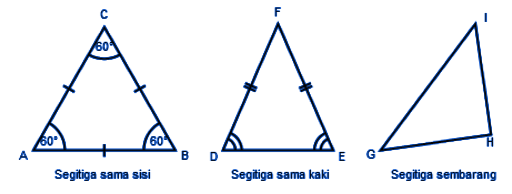
Perhatikan gambar segitiga sama kaki DEF di atas.
FD = FE
Sudut D = sudut E
Kenali lebih jauh soal segitiga sama kaki beserta rumus lengkapnya lewat artikel berikut: Rumus Segitiga Sama Kaki – Luas dan Keliling.
Segitiga Sembarang
Berbeda dengan jenis lainnya, segitiga sembarang adalah segitiga yang ketiga panjang sisinya berbeda-beda.

Perhatikan gambar di atas yang merupakan contoh segitiga sembarang. Elo liat kan, panjang sisi-sisinya berbeda.
Pelajari selengkapnya mengenai segitiga sembarang beserta rumus lengkapnya di artikel berikut: Segitiga Sembarang – Rumus Luas dan Keliling.
Jenis-Jenis Segitiga Berdasarkan Besar Sudut
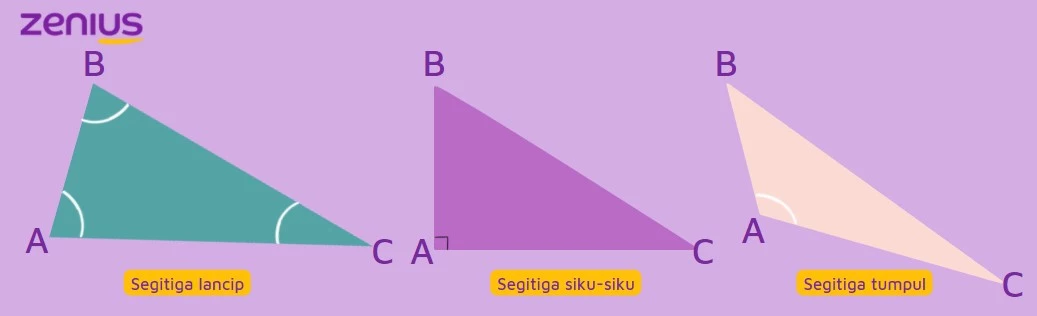
Segitiga Lancip
Segitiga lancip adalah segitiga yang masing-masing sudut besarnya kurang dari 90°.
Segitiga Tumpul
Segitiga tumpul adalah segitiga yang salah satu sudut besarnya lebih dari 90°.
Segitiga Siku-Siku
Segitiga siku-siku adalah segitiga yang salah satu sudut besarnya 90º.
Pelajari selengkapnya mengenai segitiga siku-siku beserta rumus lengkapnya di artikel berikut: Rumus Luas Segitiga Siku-siku dan Kelilingnya.
Rumus Keliling dan Luas Segitiga
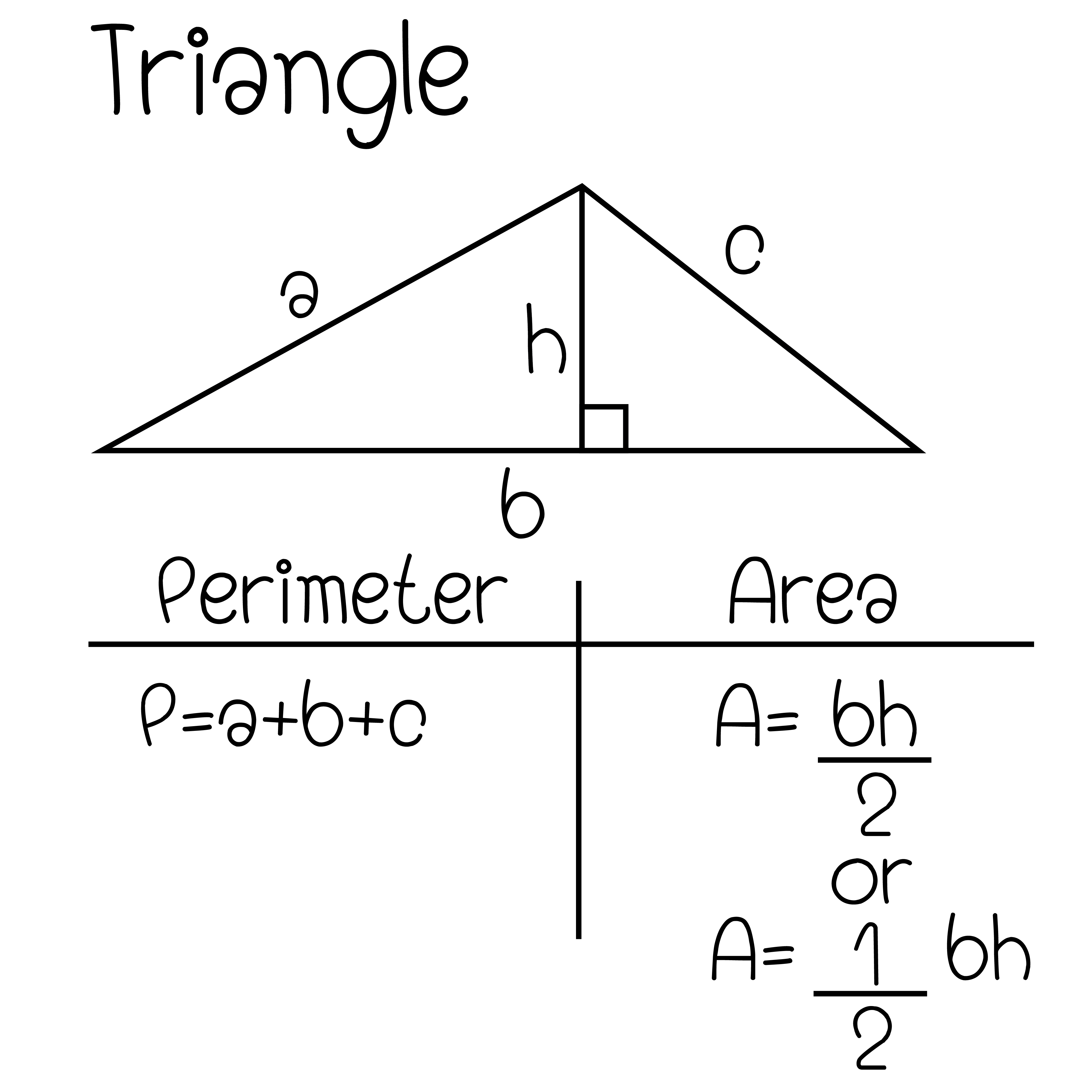
Elo perlu banget tahu cara menghitung keliling segitiga. Untuk itu elo perlu tahu nilai ketiga sisinya. Kalau sudah tau, ketiga sisi tersebut tinggal dijumlah untuk menentukan keliling segitiga (a + b + c).
Sedangkan, dalam menghitung luas segitiga, diperlukan nilai salah satu sisinya yang dianggap sebagai alas (a) serta tinggi (t) dari segitiga tersebut. Gambaran jelas rumus luas segitiga (1/2 a.t) bisa dilihat di bawah ini.
Kalau mau tahu panjang sisi miringnya, elo bisa hitung pakai dalil Phytagoras yang rumusnya bisa dilihat di ilustrasi berikut.
Kalau sudah tahu rumus keliling dan luas segitiga, yuk langsung ke contoh soal segitiga!
Contoh Soal Keliling dan Luas Segitiga (1)
Suatu segitiga sama sisi memiliki panjang alas 20 cm dan tinggi 10 cm. Hitunglah keliling dan luas segitiga tersebut!
Pembahasan
Elo lihat kan dari soal jenis segitiganya ialah segitiga sama sisi. Masih ingat dong segitiga ini punya sisi yang sama panjang di ketiga sisinya.
a = 20 cm
t = 10 cm
rumus keliling segitiga = s + s + s
=20+20+20
=60 cm
rumus luas segitiga= ½ a × t
= ½ 20 × 10
=100 cm²
Contoh Soal Keliling dan Luas Segitiga (2)
Diketahui sebuah segitiga siku-siku dengan panjang alasnya 8 cm dan tinggi 6 cm. Hitunglah keliling dan luas segitiga tersebut!
Pembahasan
Karena segitiga tersebut merupakan segitiga sama sisi, sehingga ketiga sisinya sama panjang.
a = 6 cm
t = 8 cm
Nah, contoh soal segitiga yang kali ini punya sisi yang berbeda. Berbeda dengan soal sebelumnya tentang rumus keliling segitiga sama sisi yang hanya perlu tahu salah satu sisinya saja. Segitiga siku-siku punya jumlah sisi yang berbeda.
Untuk menghitung keliling segitiga tersebut, elo perlu cari sisi miringnya terlebih dahulu dengan dalil phytagoras. Misalkan sisi miring kita simbolkan dengan c, sehingga
c² = a² + b²
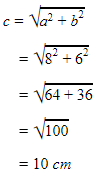
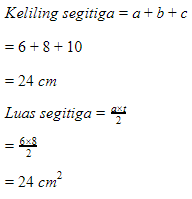
Oh iya, soal di atas juga salah satu contoh soal segitiga sembarang, lho.
Pelajari selengkapnya mengenai konsep Pythagoras dan pembahasan soalnya di sini: Cara Menggunakan Rumus Pythagoras dan Contoh Soalnya.
Contoh Soal Keliling dan Luas Segitiga (3)
Elo sudah belajar contoh soal segitiga sama sisi dan segitiga sembarangan di atas. Gue tambahin deh biar makin lancar belajar cara menghitung keliling segitiga. Kali ini gue minta elo sambil gambar segitiga sama kaki ya, biar gampang menghitungnya.
Sebuah segitiga sama kaki memiliki panjang alas berukuran 8 cm, sisi kanan dan kirinya 12 cm, dan tingginya 11 cm. Berapakah luas dan kelilingnya?
Langkah pertama, gambar segitiga sama kaki yang sudah elo buat tadi buat lagi garis di tengah-tengah segitiganya. Nah, garis lurus itu jadi tingginya. Kita mulai hitung luas segitiga pakai rumus luas segitiga ya!
a = 8 cm
t = 11 cm
s: 12 cm
Rumus luas segitiga : ½ x alas x tinggi
= ½ x 8 x 11
= 44 cm
Rumus keliling segitiga: s+s+s
= 12 + 12 + 8
=32 cm
Gimana nih sekarang, sudah mengerti kan cara menghitung keliling dan luas segitiga? Jadi begitulah penjelasan mengenai jenis-jenis segitiga, rumus luas dan keliling segitiga beserta contoh soal segitiga.
Nah, sekarang elo jadi lebih tahu kan jenis-jenis segitiga dan cara menghitung segitiga. Sudah belajar juga kan lewat contoh soal keliling segitiga dan contoh soal luas segitiga? Terus dilatih ya, jangan sampai lupa.
Rumus segitiga termasuk dalam ragam rumus bangun datar. Untuk belajar rumus luas dan keliling bangun datar lain, kamu bisa baca dua artikel ini: Rumus Luas Bangun Datar & Rumus Keliling Bangun Datar.
***
Untuk elo yang ingin belajar lebih tentang segitiga dan bangun datar lainnya, bisa lihat video materi di bawah ini ya. Eits, tenang saja, videonya asyik dan enggak bosenin kok. Dijamin gampang ngerti deh.
Belajar Tentang Segitiga: Rumus, Luas, dan Keliling
Berani sekalian ngetes skill matematika? Nih, cobain Zencore! Dengan fitur adaptive learning, kamu bisa tau seberapa jago kemampuan fundamental lewat kuis CorePractice, sekaligus upgrade otak biar makin cerdas! Ketuk banner di bawah buat cobain!
Updated by: Silvia Dwi











🗿👍