Apabila ada orang berdiri di dalam kereta yang sedang melaju, lalu dia melompat ke atas, di mana dia akan jatuh? Jawabannya dibahas dengan penjelasan konsep Gerak Parabola.
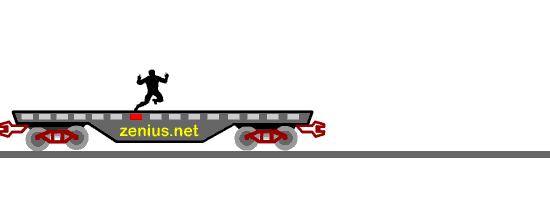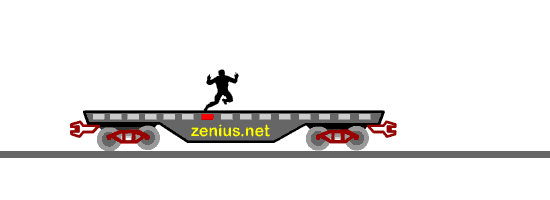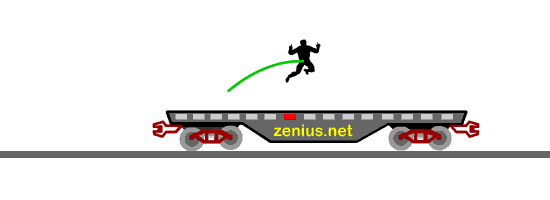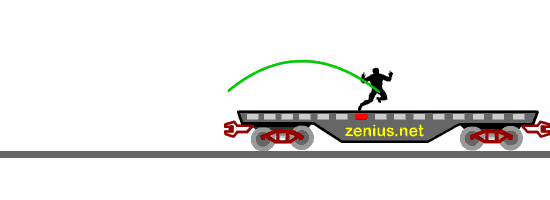
Ada Quiz nih. Perhatiin gambar di bawah ini. Ini adalah gambar kereta yang ceritanya lagi melaju ke kanan dengan laju 30m/s. Terus, ada orang berada di dalam kereta dan sedang berdiri menghadap ke depan kereta. Pertanyaannya: Kalau dia lompat vertikal ke atas, di mana dia akan jatuh?
(A) Jatuh di belakang tempat dia melompat (B) Jatuh di tempat yang sama dengan tempat dia melompat (C) Jatuh di depan tempat dia melompat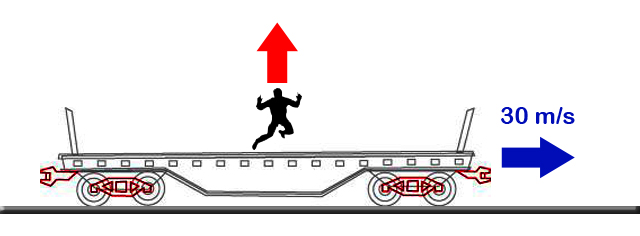
=======================================================================
Daftar Isi
EIT SEBELUM KAMU SCROLL KE BAWAH, COBA DIPIKIRIN DULU JAWABANNYA YAH!
Oke, jadi jawabannya yang bener adalah yang….. (B). Jatuh di tempat yang sama dengan tempat lo melompat.
Untuk pertanyaan semacam ini, banyak banget sih yang jawab (A), jatuh di belakang tempat melompat. Karena banyak yang mikirnya kalau kita lompat ke atas, kereta akan melaju dan meninggalkan posisi kita.
Nah, tapi sekarang coba pikirin tentang ini: Kalau kita lompat vertikal ke atas di atas bumi, apakah kita jatuh di tempat yang sama juga dengan tempat kita melompat? Cobain aja (Try it! Seriously 🙂 ). Padahal bumi itu bergerak lebih cepat dibandingkan kereta loh. Btw, berapa sih kecepatan bumi?
Kita tahu kalau Jari-jari bumi itu adalah: 6371 km
Kalau gitu kecepatan bumi (untuk di ekuator) bisa diperoleh dengan cara:
Yeap. Jauh lebih cepat dari kecepatan kereta di contoh di atas.
Meskipun bumi itu berputar dengan kecepatan yang cepet banget, kita tetep jatuh di tempat yang sama kan setiap kali kita melompat ke atas? Nah, sama juga dengan lompat di atas kereta. Kita juga akan jatuh di tempat yang sama.
Kenapa Bisa Jatuh Di Tempat Yang Sama?
Okay, kita udah tau kalau jawabannya (B). Sekarang, penjelasannya apa nih? Pertama, kita inget-inget dulu Hukum Newton I tentang Gaya: Jika total gaya yang bekerja pada sebuah benda itu adalah nol, maka benda tersebut pasti diam atau bergerak dengan kecepatan konstan.
ΣF = 0
Nah, hukum ini bisa kita kerjakan secara terpisah untuk sumbu-x dan untuk sumbu-y. Pada Quiz yang kita kerjain ini, orang melompat ke atas dan mengalami gaya gravitasi, sehingga sigma F di sumbu-y nggak nol. Tapi untuk arah sumbu-x, sigma F-nya sama dengan nol. Nggak ada gaya apa-apa di arah horizontal. Sehingga persamaannya bisa kita tulis lagi seperti ini:
ΣFx = 0
Sekarang, coba lihat lagi gambar tadi. Kereta bergerak dengan kecepatan 30m/s kan? Kecepatannya konstan. Sehingga, orang di dalam kereta jika diamati dari luar kereta juga bergerak dengan kecepatan konstan, 30m/s juga.
Nah, ketika orang ini melompat ke atas, tidak ada gaya horizontal yang bekerja pada orang ini. Jadi, sigma F untuk sumbu-x juga nol. Akibatnya, setelah orang ini melompat dan berada di udara pun, orang ini tetap memiliki kecepatan arah sumbu-x yang konstan sebesar 30m/s.
Jadi, kecepatan orang ini (untuk arah sumbu-x) sama dengan kecepatan kereta. Sehingga jarak horizontal yang ditempuh oleh orang ini akan sama dengan jarak horizontal yang ditempuh oleh kereta. Inilah yang mengakibatkan orang ini jatuh di tempat yang sama di tempat dia melompat.
Gerak Parabola
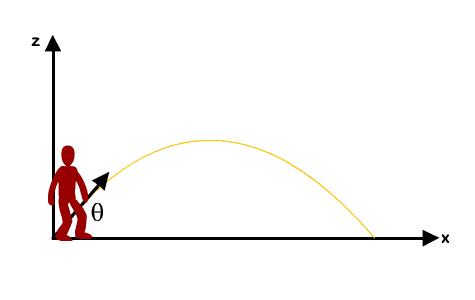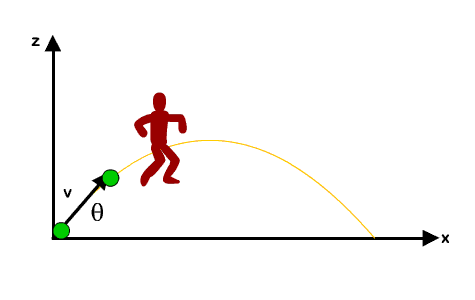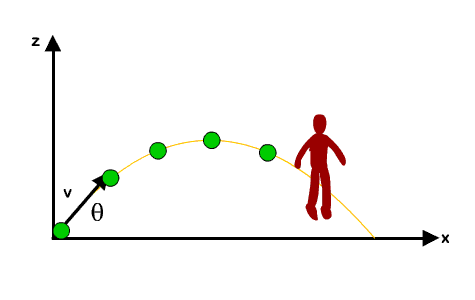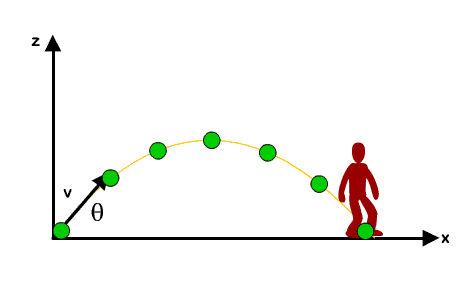
Kalau kita analisis lagi lebih mendalam, gerak orang ini sebenarnya merupakan gerak parabola. Karena pada arah horizontal, gerakannya adalah GLB (a = 0, v konstan) sementara pada arah vertikal, gerakannya adalah GLBB (a = konstan, v berubah beraturan).
Pada sumbu-y (vertikal), orang ini bergerak dengan kecepatan awal tertentu dan arahnya ke atas (namanya juga melompat, ya ke atas lah ya). Nah, tapi kecepatannya ini nggak konstan, melainkan dia berubah secara beraturan karena orang ini ditarik dengan gaya gravitasi. Sehingga, dia punya percepatan arah ke bawah, yaitu percepatan gravitasi, besarnya g = 10m/s2.
Buat yang pengen belajar lebih detil tentang gerak parabola, bisa tonton itu di sini:
– Latihan Soal untuk Gerak Parabola
Pertanyaan Diskusi
Nah, terakhir nih. Misalkan soalnya sama kayak soal di atas, tapi kereta bergeraknya nggak konstan. Dia bergerak dengan kecepatan dengan persamaan v = 2t + 10. Pada saat t =2, lo melompat vertikal ke atas. Di mana lo akan jatuh? Diskusiin di comments aja yah. Sebutin juga alasannya kenapa yah..
Sering nemu soal matematika yang sulit kamu jawab? Santai aja boy, nih kenalin ZenBot, temen 24 jam yang siap bantu kamu cari solusi dari masalah matematika! Untuk menjawab soal-soal tentang matematika, kamu juga bisa manfaatkan fitur dari ZenBot, lho! Tanyain soal yang kamu gak bisa jawab lewat chat WhatsApp ZenBot sekarang atau download aplikasi Zenius.










btw gaya gesek angin ga bekerja ya bang?
kga jadi lupa di dalem orangnya :))
Iya, karena orangnya di dalam kereta, anggap nggak ada gesekan dengan udara.
gesekan rel kereta ga di itung bang? ahaha :))
Jatuh di belakang tempat dia lompat, alesannya kecepatan kereta tepat pada saat melompat (t=2) adalah V(2) = 2(2) + 10 = 14 m/s sedangkan pada saat selesai lompat adalah 2(2.8)+10 = 15.6 m/s dimana t dicari dari ( Vo/g ) x 2 (T pada saat dipuncak x 2). (14/10) x 2 = 2.8. Bener atau engganya auamat yah hahaha.
Yoi… bener. Sebenernya alasannya simple aja: kalau persamaannya V = 2t + 10, berarti kereta mengalami percepatan (Vnya naik terus). Ketika orang tersebut lompat, dia masih dalam kecepatan V. Pas orang itu di udara, kereta bergerak lebih cepat, sehingga orang itu ketinggalan.
gimana solusinya guru yang mngajarkan dengan metode menghafal formula / rumus. terpaksa gue mau gak mau harus ngapalin rumus padahal formula / rumus banyak banget sampai detail pula. padahal belajar dengan konsep lebih baik daripada belajar dengan menghafal formula / rumus.
jadi solusinya gimana mengatasi guru sekolah yang seperti ini ??
Waktu SMA sih gue juga pernah ketemu guru yang kayak gitu. Rasanya muak banget. Hehehe… Kalau ketemu guru yang kayak gini, jangan ikut-ikutan ngafalin rumus. Sebisa mungkin semua rumus yang disuruh dihafal sama guru lo itu, lo turunin sendiri. Nanti lama-lama hafal sendiri sih kalau lo sering nurunin rumus itu, dan malah lebih ngerti konsepnya dibanding sama yang cuma menghafal.
Btw, di social media ada yang ngomong ke gue kalau dia nyoba2in lompat di kereta. Bahkan ada yang nyobain lompat di mobil bak segala. Hehehe… Sebenernya ada cara yang lebih aman buat bikin percobaan di atas. Saran gue:
(1) Beli Balon, terus tiup secukupnya (jangan diisi pake helium, nanti dia ga jatuh)
(2) Naik mobil dengan kecepatan konstan. Pastiin kalau kecepatannya konstan yah, nggak ada percepatan, nggak ada perlambatan.
(3) Pastiin nggak ada jendela yang terbuka, jadi nggak ada udara yang bergerak.
(4) Pegang balon itu di dalam mobil, terus lepasin vertikal ke atas, pelan aja.
Kalau percobaan ini dilakuin dengan bener, lo akan lihat balon tersebut jatuh di posisi tempat lo melepasnya. Karena kalau dari luar, gerak balon tersebut adalah gerak parabola.
tapi kok kalo saya liat difilm2 / game (gapernah liat langsung 😀 ) waktu ada bomb dijatuhin dari pesawat, kok bombnya jatuh di depan dimana bomb itu dijatuhin ya? jadi waktu jatuh itu bombnya kaya sambil maju juga. jelasin dong 😀